APPENDIX D HUMAN HEALTH ANALYSIS
D.1 INTRODUCTION
The basic approach used in assessing human health impacts was to first identify the affected environments and establish a baseline representing the risk from current operations. This baseline was primarily established from empirical data (e.g., annual environmental reports, occupational incident rates, and worker exposure records). Next, changes in this baseline risk resulting from the Proposed Action, No Action, and Pit Storage Relocation Alternatives were examined to ascertain the human health impacts of the alternatives.
Radiological impacts on human health are an important consideration in establishing the baseline risk and estimating changes to it. The impact of radiation on human health is the topic of section D.2.
Assessing the human health impacts of the alternatives involved a four-step process. The first step was to identify a broad spectrum of potential accident scenarios. These scenarios were obtained from available, site-specific safety and environmental documents.
The second step in the process used screening techniques to identify the specific scenarios that dominate risk (i.e., scenarios that contribute an appreciable fraction of the total risk). This is described in section D.3.
Due to the large number of potential accident scenarios that could impact human health, it is impractical to evaluate all of them in detail. This is a common problem encountered in risk assessments. The standard approach is to apply scoping calculations during the screening step. Rigorous evaluations (the third step in the process) were only performed for the risk-dominant scenarios identified in step two. Section D.4 addresses the methodology used to evaluate the risk dominant scenarios.
The fourth and final step in assessing the human health impact of the alternatives was to evaluate the risk from normal operations (i.e., the risk if no accidents occur). This is the topic of section D.5. Consequence uncertainties in the assessment are the topic of section D.6.
D.2 RADIOLOGICAL IMPACTS ON HUMAN HEALTH
This section addresses the human health impacts resulting from exposure to radiation. The nature of radiation, its effects on human health, and the sources of radiation pertinent to this EIS are examined.
D.2.1 Nature of Radiation and Its Effects on Humans
For a uniform irradiation of the body, the incidence of cancer varies among organs and tissues; the thyroid and skin demonstrate a greater sensitivity than other organs. However, such cancers also produce relatively low mortality rates because they are relatively amenable to medical treatment. Because of the readily available data for cancer mortality rates and the relative scarcity of prospective epidemiologic studies, somatic effects leading to cancer incidence are presented in this EIS. The number of cancer fatalities can be used to compare the risks among the various alternatives.
The National Research Council's Committee on the Biological Effects of Ionizing Radiations has prepared a series of reports to advise the U.S. Government on the health consequences of radiation exposures. The latest of these reports, Health Effects of Exposure to Low Levels of Ionizing Radiation BEIR V, published in 1990, provides the most current estimates for excess mortality from leukemia and cancers other than leukemia expected to result from exposure to ionizing radiation (NAP 1990). The BEIR V report updates the models and risk estimates provided in the earlier report of the BEIR III Committee published in 1980. BEIR V models were developed for application to the U.S. population.
D.2.1.1 Risk Estimates for Doses Received During Normal Operation
For low doses and dose rates, a linear-quadratic model was found to provide a significantly better fit to the data for leukemia than a linear one, and leukemia risks were based on a linear-quadratic function. This reduces the effects by a factor of two over estimates that are obtained from the linear model. For other cancers, linear models were found to provide an adequate fit to the data, and were used for extrapolation to low doses. However, the BEIR V Committee recommended reducing these linear estimates by a factor between 2 and 10 for doses received at low dose rates. For this EIS, a risk reduction factor of two was adopted for conservatism.
Based on the above discussion, the resulting risk estimator would be equal to half the value observed for accident situations or approximately 500 excess fatal cancers per million person-rem (0.0005 excess fatal cancers per person-rem). This is the risk value used in this EIS to calculate fatal cancers to the general public during normal operations. For workers, a value of 400 excess fatal cancers per million person-rem (0.0004 excess fatal cancers per person-rem) is used. This lower value reflects the absence of children in the workforce.
The risk estimates may be applied to calculate the effects of exposing a population to radiation. For example, in a population of 100,000 people exposed only to natural background radiation (0.3 rem per year), 15 latent cancer fatalities per year would be inferred to be caused by the radiation (100,000 persons x 0.3 rem per year x 0.0005 latent cancer fatalities per person-rem = 15 latent cancer fatalities per year).
How should one interpret a nonintegral number of latent cancer fatalities, such as 0.05? The answer is to interpret the result as a statistical estimate. That is, 0.05 is the average number of deaths that would result if a total dose of 0.001 rem were applied to many different groups of 100,000 people. In most groups, no person (0 people) would incur a latent cancer fatality from the 0.001 rem dose each member would have received. In a small fraction of the groups, one latent fatal cancer would result; in exceptionally few groups, two or more latent fatal cancers would occur. The average number of deaths over all the groups would be 0.05 latent fatal cancers (just as the average of 0, 0, 0, and 1 is 1/4, or 0.25). The most likely outcome is zero latent cancer fatalities.
These same concepts apply to estimating the effects of radiation exposure on a single individual. Consider the effects, for example, of exposure to background radiation over a lifetime. The "number of latent cancer fatalities" corresponding to a single individual's exposure over a (presumed) 72-year lifetime to 0.3 rem per year is the following:
1 person x 0.3 rem/year x 72 years x
0.0005 latent cancer fatalities/person-rem
= 0.011 latent cancer fatalities.
Again, this should be interpreted in a statistical sense; that is, the estimated effect of background radiation exposure on the exposed individual would produce a 1.1 percent chance that the individual might incur a fatal cancer caused by the exposure. Presented another way, this method estimates that approximately 1.1 percent of the population might die of cancers induced by background radiation.
Although health risk factors are statistical factors, and therefore not strictly applicable to individuals, they have been used in the past to estimate the incremental risk to an individual from exposure to radiation. Therefore, the factor of 0.0005 and 0.0004 per rem of individual committed effective dose equivalent for a member of the public and for a worker, respectively, have also been used in this EIS to calculate the individual's incremental fatal cancer risk from exposure to radiation.
For the public, the health effects expressed in this EIS are the number of fatal cancers to the population within 80 kilometers (50 miles) from exposure to radioactivity released from the site. For workers, the health effects expressed are the risk to the average worker at a site and the number of fatal cancers to all workers at that site.
D.2.2 Sources of Radiation
The sources of radiation pertinent to this EIS can be classified as background (i.e., the radiation to which workers and the public are exposed exclusive of all radiation sources at Pantex Plant and the alternative sites) or site-specific in origin. With respect to background radiation, on the average, Americans receive a total of about 350 millirem per year from all sources of radiation, both natural and man-made. The sources of radiation can be divided into six different categories: cosmic radiation, external terrestrial radiation, internal radiation, consumer products, medical diagnosis and therapy, and other sources. Each category is discussed below.
Cosmic radiation is ionizing radiation resulting from energetic charged particles from space continuously hitting the earth's atmosphere. These particles and the secondary particles and photons they create are cosmic radiation. Because the atmosphere provides some shielding against cosmic radiation, the intensity of this radiation increases with altitude above sea level.
External terrestrial radiation is the radiation emitted from the radioactive materials in the earth's rocks and soils. The average annual dose from cosmic and external terrestrial radiation is about 55 millirem. The cosmic and external terrestrial radiation for the sites in this EIS ranges from about 70 to 120 millirem per year.
Internal radiation arises from the human body metabolizing natural radioactive material which has entered the body by inhalation or ingestion. Natural radionuclides in the body include isotopes of uranium, thorium, radium, radon, polonium, bismuth, potassium, rubidium, and carbon. The major contributor to the annual dose equivalent for internal radioactivity are the short-lived decay products of radon which contribute about 200 millirem per year. The average dose from other internal radionuclides is about 39 millirem per year.
Consumer products also contain sources of ionizing radiation. In some products, like smoke detectors and airport x-ray machines, the radiation source is essential to the products' operation. In other products, such as television and tobacco, the radiation occurs incidentally to the product function. The average annual dose from all consumer products is about 10 millirem.
Radiation is an important diagnostic medical tool and cancer treatment. Diagnostic x-rays result in an average annual exposure of 39 millirem. Nuclear medical procedures result in an average annual exposure of 14 millirem.
There are a few additional sources of radiation that contribute minor doses to individuals in the U.S. The dose from nuclear fuel cycle facilities such as uranium mines, mills and fuel processing plants, nuclear power plants and transportation routes has been estimated to be less than 1 millirem per year. Radioactive fallout from atmospheric atomic bomb tests, emissions of radioactive material from DOE facilities, emissions from certain mineral extraction facilities, and transportation of radioactive materials contribute less than 1 millirem per year to the average dose to an individual. Air travel contributes approximately 1 millirem per year to the average dose.
The collective (or population) dose to an exposed population is calculated by summing the estimated doses received by each member of the exposed population. This total dose received by the exposed population is measured in person-rem. For example, if 1,000 people each received a dose of 1 millirem (0.001 rem), the collective dose is 1,000 persons x 0.001 rem = 1.0 person-rem. Alternatively, the same collective dose (1.0 person-rem) results from 500 people each of whom received a dose of 2 millirem (500 persons x 2 millirem = 1 person-rem).
Site-specific sources of radiation are industrial sources and sources associated with nuclear weapons. The industrial sources are used to generate x-rays and gamma rays for non-destructive examinations of weapon components. Exposure to these sources of radiation only poses a potential risk to workers. However, since nondestructive examination using x-rays and gamma rays is a well established industrial practice, this contribution to worker risk is negligible.
The sources of radiation associated with nuclear weapons include tritium, uranium, and plutonium. Tritium is a radioactive form of hydrogen. By itself, its effects on human health are relatively modest. However, tritium can combine with hydrogen and oxygen to form a radioactive molecule that chemically mimics ordinary water. In this form tritium is readily assimilated by living tissue, which is subsequently irradiated as the tritium decays. This represents the most toxic form of tritium, and is especially a concern if the release involves a fire (which converts most of the tritium into the radioactive form of water).
Uranium is present at Pantex Plant both in the enriched and depleted forms. Enriched uranium contains a high percentage (up to 93 percent) of the 235 isotope, while depleted uranium is mostly the 238 isotope. Although uranium is toxic, its toxicity is so low relative to plutonium that its relative risk to workers and the public is negligibly small.
Plutonium is present in pits and radioisotopic thermoelectric generators (RTGs). The predominant plutonium isotope in pits is 239, while the 238 isotope is used as the RTG power source. Due to their highly robust design and construction, RTGs pose only a negligible risk to workers and the public.
Plutonium poses two principal human health risks: direct exposure to workers involved in disassembly and transportation activities; and a potential inhalation hazard to workers and the public if it is accidentally released and disperses as respirable particles. To be respirable, plutonium particles must be smaller than 10 microns. Particles larger than 10 microns are too large to disperse deeply into the lungs. As a result, they have a relatively short residence time and essentially cause no adverse health effects.
Inhaled plutonium particles smaller than 10 microns are not cleared from the lungs by normal bodily processes. This results in a potentially significant alpha dose to the lungs. Moreover, the plutonium will eventually cross the capillaries into the bloodstream. Once in the bloodstream, the plutonium eventually accumulates at the interface between hard bone and the marrow. Hence, the two most vulnerable organs to plutonium inhalation are the lungs and bone marrow. Both workers and the public are vulnerable to plutonium inhalation if an accident occurs that disperses it as respirable particles (e.g., a fire or explosion). Plutonium inhalation is not a concern during normal operations because the plutonium is always contained.
D.3 SCENARIO SCREENING
Ideally, a complete risk assessment would express the total human health risk as the sum of all potential accident scenarios. Since it is impractical to rigorously quantify all of the terms in the ideal summation, the purpose of a screening methodology is to identify a subset of the terms such that the summation over this subset constitutes a large fraction (e.g., >95 percent) of the total risk.
The basic facility risk screening methodology used for the Pantex EIS is explained in section D.3.1. This basic methodology identifies the risk dominant potential accident scenarios that require a rigorous analysis in the EIS. A description of the methodology application is presented in section D.3.2.
D.3.1 Screening Methodology
Ideally, a complete risk assessment would express the total facility risk for a particular endpoint, RT, as the summation:
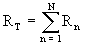
(Eq. D-1)
where there are a total of N scenarios contributing to the risk. Rather than rigorously quantify all N terms in Equation D-1, the purpose of the screening methodology was to identify a subset of the N terms such that the summation over this subset, N', satisfies the relation:
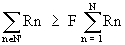
(Eq. D-2)
where F is some large fraction (e.g., >0.95).
Three endpoints for which the screening methods were applied are:
- Potential direct exposure of workers or the public to radiation and hazardous chemicals as a result of continued operations or change in mission.
- Risk from an accidental release of radionuclides or hazardous chemicals as a result of continued operations or change in mission.
- Potential latent cancer fatalities as a result of continued operations or change in mission.
The first endpoint required addressing the quantities of radiation and hazardous chemicals to which workers or the public are exposed, regardless of the health effects associated with the exposure. The risk from accidental releases stated in the second endpoint definition is interpreted as the risk of fatalities. Quantifying the second and third endpoints necessitated examining both the amount of exposure and the health effects (in terms of the likelihood of a resultant fatality) associated with the exposure.
Risks associated with potential accident scenarios were quantified using probabilistic risk assessment (PRA) techniques. These techniques expressed risk as the product of two parameters:
ln - the frequency (per year) that scenario "n" is expected to occur.
Cn - the consequence (e.g., fatal cancers) associated with the occurrence of scenario "n".
The screening methodology used to identify risk dominant potential accident scenarios was predicated upon DOE 1994, DOD 1977, Jones 1988, and DH 1993. Essentially, it involved developing a risk matrix that divided the frequency and consequence ranges into a finite number of categories. The selected frequency categories were from criteria tabulated in DOE 1994:
- Anticipated (ln > 10-2 per year).
- Unlikely (10-2 per year > ln > 10-4 per year).
- Extremely unlikely (10-4 per year >ln > 10-6 per year).
- Not reasonably foreseeable (10-6 per year > ln)
DOE 1994 does not address consequence categories. However, the consequence categories cited in DOD 1977, Jones 1988, and DH 1993 are:
- Catastrophic (consequences cause deaths).
- Critical (consequences cause severe injuries or occupational illnesses).
- Marginal (consequences cause minor injuries or occupational illnesses).
- Negligible (consequences corresponding to no injuries nor occupational illnesses).
The definitions in DOD 1977, Jones 1988, and DH 1993 include environmental consequences and facility damage. Although these additional consequences exceed the endpoint definitions, any potential accident scenario that can appreciably impact the environment or damage a facility is capable of contributing to the risk of a human receptor and was included in the screening process.
Figure D.3.1-1 depicts the risk matrix developed from these frequency and consequence categories. Since:
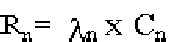
(Eq. D-3)
it is evident from Figure D.3.1-1 that for a given frequency category, the dominant risk scenarios are those assigned to the highest consequence category. This resulted in the following risk screening process:
- Identification of anticipated scenarios. Those facility-specific, hazard-specific scenarios assigned to the highest consequence category were selected as risk dominant. This consequence was designated category C' (e.g., the marginal category).
- Examination of the unlikely scenarios. If none of these scenarios belonged to a consequence category higher than C', there are no risk dominant scenarios with unlikely frequencies. If some unlikely scenarios belonged to a consequence category higher than C', these facility-specific, hazard-specific scenarios were also risk dominant. If some unlikely scenarios belonged to a consequence category higher than C', then C' designated this higher consequence category (e.g., the critical category).
- Examination of the extremely unlikely scenarios. If none of these scenarios belonged to a consequence category higher than C', there were no risk dominant scenarios with extremely unlikely frequencies. If some extremely unlikely scenarios belonged to a consequence category higher than C', these facility-specific, hazard-specific scenarios were also risk dominant. If some extremely unlikely scenarios belonged to a consequence category higher than C', than C' designated this higher consequence category.
- Examination of the not reasonably foreseeable scenarios. If none of these scenarios belonged to a consequence category higher than C', there were no risk dominant scenarios with not reasonably foreseeable frequencies. If some not reasonably foreseeable scenarios belonged to a consequence category higher than C', these facility-specific, hazard-specific scenarios were also risk dominant.
These four steps constitute the process developed for screening risks associated with potential accident scenarios. To the extent practical, frequency categories and consequence categories were assigned using results from applicable risk studies. When applicable PRA results were unavailable, scoping calculations were used to assign scenarios to appropriate frequency and consequence categories.
Figures D.3.1-2 and D.3.1-3 further illustrate the risk screening process. A large X in Figure D.3.1-2 symbolizes that some scenarios have been assigned to a particular risk matrix category. Specifically, Figure D.3.1-2 indicates that:
- All anticipated scenarios have negligible consequences.
- Unlikely scenarios have negligible, marginal, or critical consequences.
- The extremely unlikely scenarios have marginal, critical, or catastrophic consequences.
- All not reasonably foreseeable scenarios belong to either the critical or catastrophic consequence categories.
Beginning with the anticipated scenarios, all of them are selected as risk dominant (since they all belong to the same consequence category) using the risk screening process. This selection is depicted by the large circle surrounding the X representing this set of scenarios in Figure D.3.1-3.
Examining the unlikely scenarios disclosed that those assigned to the marginal and critical consequence categories are risk dominant because, even though they are far less likely than the anticipated scenarios, their consequences are greater. However, the unlikely scenarios with negligible consequences are not significant risk contributors. Since each frequency category spans at least two orders of magnitude, the frequency of an unlikely scenario will typically be an order of magnitude or more less than an anticipated scenario. Thus, given an anticipated scenario and an unlikely scenario assigned to the same consequence category, the anticipated scenario risk is typically an order of magnitude or more greater than the risk from the unlikely scenario.
Applying this same reasoning to the extremely unlikely scenarios showed that only those with catastrophic consequences are risk dominant. None of the scenarios assigned to the not reasonably foreseeable frequency category are risk dominant in Figure D.3.1-3.
The result of this risk screening process is a set of risk dominant scenarios that required detailed analysis. In the context of Equations D-1, D-2, and D-3, the screening process exhibited in Figures D.3.1-1 through D.3.1-3 is an inferential approach for satisfying Equation D-2.
Figure D.3.1-1. Risk Matrix for Potential Accident Scenario
Figure D.3.1-2. Risk Matrix with Scenarios Assigend to Frequency and Consequence Categories
Figure D.3.1-3. Risk Matrix with Scenarios Identified for Detailed Evaluation
The basic screening methodology embodied in Equation D-2 is a relative risk approach. That is, it identified potential accident scenarios that contribute significantly to the overall facility risk without regard to scenario likelihood or consequence. Thus, it spans the spectrum from high probability-low consequence scenarios to those with extremely low occurrence probabilities, but large consequences. This approach differs from some conventional methods that screened low frequency scenarios without regard to their potential consequences (e.g., DOE 1992a). The typical justification for screening low frequency scenarios without regard to their potential consequences was that such scenarios are not reasonably foreseeable.
An important consideration in applying Equation D-3 is the contribution
of the uncertainties inherent in frequency assessments involving
numerous conditional probabilities. This consideration is important
to provide confidence in the risk estimates (i.e., the product
of the scenario frequency and consequence) and to ensure that
no potentially risk dominant scenarios are excluded from consideration
due to large uncertainties in their assessed frequency. A practical
solution to this concern is to use a statistic for the frequency
assessment that is relatively easy to calculate, but that also
provides confidence that the frequency is not underestimated.
The mean frequency is such a statistic. Although the actual
impact of inherent uncertainties requires application-specific
analyses, the importance of this concern can be illustrated by
considering a single scenario with frequency,
ln. In general:
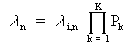
(Eq. D-4)
Here:
- li,n is the initiating event frequency for scenario "n".
- Pk is the conditional probability of the kth event that must occur in scenario "n".
- There are a total of K conditional probabilities needed to quantify the scenario frequency.
Uncertainty distributions for the parameters usually encountered in PRAs are lognormal with uncertainty factors (defined as the ratio of the 95th percentile to the median) in the range 2 to 10. Figures D.3.1-4 through D.3.1-6 depict the degree of confidence one can have on the value of ln, depending on the number of conditional probabilities in Equation D-4, the statistical values used for each parameter, and the uncertainty factors. A nominal frequency of 10-7 per year is used in Figures D.3.1-4 through D.3.1-6, since this represents a not reasonably foreseeable scenario (i.e., a scenario which will typically have large uncertainty). In Figures D.3.1-4 and D.3.1-5 the nominal value corresponds to the mean frequency.
Figure D.3.1-4 shows the mean and 95th percentile (i.e., values where there is 95 percent confidence that they exceed the actual frequency) as a function of the number of conditional probabilities in Equation D-4. If there are no conditional probabilities in the scenario:
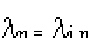
(Eq. D-5)
and there is 95 percent confidence that the actual frequency is less than 2.4 x 10-7 per year. Although the 95th percentile first increases, then decreases with K, Figure D.3.1-4 demonstrates that if all of the variables in Equation D-4 have uncertainty factors of 3, there is at least 95 percent confidence that the actual frequency exceeds the mean by no more than a factor of 4.
Uncertainty factors of 10 are used in Figure D.3.1-5. Here, the 95th percentile is actually less than the mean when K exceeds 4. This represents a fundamental property of the lognormal distribution-as the overall uncertainty increases the chances of exceeding the mean diminish. Also, Figure D.3.1-5 discloses that there is at least 95-percent confidence that the actual frequency exceeds the mean by no more than a factor of 4.
Figure D.3.1-6 compares the median (instead of the mean) to the 95th percentile. As in Figure D.3.1-4, an uncertainty factor of 3 is assigned to the variables in Equation D-4. Notice that as the number of conditional probabilities increases, the ratio of the 95th percentile to the median continually increases to over one and one half orders of magnitude.
The crucial difference between Figures D.3.1-4 and D.3.1-6 is that different statistical representations of the nominal frequency are used-the mean in Figure D.3.1-4 and the median in Figure D.3.1-6. This suggests that while there is reasonable confidence that the actual scenario frequency will not exceed the mean value, there can be an appreciable chance that the actual scenario frequency exceeds the median value.
Conclusions obtained from Figures D.3.1-4 through D.3.1-6 are only strictly applicable to situations involving the products of lognormally distributed parameters. Fortunately, such situations are commonly encountered in PRAs. However, caution must be exercised when estimating confidence levels for calculations differing from Equation D-4.
D.3.2 Screening Methodology Application
Table D.3.2-1 contains the risk dominant scenarios for Pantex Plant. These are the scenarios that remained after the section D.3.1 methodology was applied to the candidate scenarios in Table D.3.2-2. Using frequency and consequence estimates from available plant safety and environmental documents, the Table D.3.2-2 scenarios were grouped into the appropriate risk matrix categories. Since it is somewhat difficult to directly compare the consequences of all scenarios together, candidate scenarios involving radionuclide hazards, chemical hazards, and high explosive (HE) hazards were considered separately. The risk dominant scenarios for each of these three hazards appear in Table D.3.2-1 for Pantex Plant.
Table D.3.2-1 Risk-Dominant Scenarios for Pantex Plant (.pdf)
Table D.3.2-2 Candidate Accident Scenarios for Pantex Plant (.pdf)
This same process was applied to the alternative sites. Since only relocation of pit storage is being considered at these alternative sites, many of the candidate scenarios in Table D.3.2-1 are inapplicable. For example, candidate scenario C40 in Table D.3.2-2 is applicable to pit storage at an alternative site (although the facility designations in Table D.3.2-2 would have to be modified to the appropriate facility at the alternative site-e.g., P-Reactor at the Savannah River Site). However, candidate scenario C2 in Table D.3.2-2 is inapplicable to the alternative sites since there will be no relocation of tritium. Similarly, candidate scenarios involving HE fires and explosions or hazardous chemicals are inapplicable to the alternative sites. Candidate scenarios particularly applicable to pit storage at the alternative sites are footnoted in Table D.3.2-2.
Relative to the hazards considered for Pantex Plant, the only hazardous material applicable to alternative sites is pits. Moreover, the only significant risk to these pits during normal operations is the risk from a forklift accident during transfer operations when the pits are being placed into storage.
All of the external events and natural phenomena considered for Pantex Plant are included in the candidate scenarios for alternative sites. In addition, some site-specific natural phenomena were added. When the relative risks from a forklift accident and candidate scenarios initiated by external events or natural phenomena are compared, the forklift accident is risk dominant at all alternative sites (with the possible exception of earthquakes at Manzano Weapons Storage Area [WSA]).
There are two reasons why forklift accidents are risk dominant at the alternative sites. First, fewer facilities are at risk at the alternative sites than at Pantex. For example, the Zone 4 storage magazines, as well as the Zone 12 bays, cells, and support facilities, are included in the aircraft accident analysis at Pantex Plant. Except for Manzano WSA, the number of facilities at risk, plus the intensity of aircraft traffic (especially aircraft capable of causing facility damage) is significantly higher at Pantex Plant than at the alternative sites.
At Manzano WSA, the rock overburden reduces the likelihood that an aircraft impact could cause a release from the candidate storage facilities to a negligible level (see section E.3.2.2). Therefore, the frequency of a radionuclide release caused by an aircraft impact is significantly lower at the alternative sites. Although the consequences resulting from a radionuclide release initiated by an aircraft impact are potentially greater than the consequences resulting from a forklift accident, the risk (expressed as the product of frequency and consequence) from aircraft impacts at the alternative sites is a small fraction of a percent relative to the risk associated with a forklift accident (with the possible exception of earthquakes at Manzano WSA).
The risk from natural phenomena at Pantex Plant is dominated by earthquakes. This is not a result of potential earthquake damage to storage magazines, but rather is due to the possibility of seismic damage to certain support facilities that were erected in the late 1940's and 1950's (and which could be replaced by proposed facility construction and upgrades at Pantex Plant as described in appendix H). In terms of relative risk, the contribution to the risk at Pantex Plant from external events that threaten the Zone 4 storage magazines is negligible. With respect to pit storage, this low relative risk is due to the robust construction of the magazines and the integrity of the AT-400A shipping containers. A similar situation exists at the alternative storage sites, and is the second reason why forklift accidents are risk dominant at the alternative sites (with the possible exception of earthquakes at Manzano WSA). Figure D.3.2-7 illustrates this concept.
Occurrence of an external event or natural phenomenon is the initiating event in Figure D.3.2-7. Given that the initiating event occurs, a release from the stored pits is only possible if facility damage results from the initiating event. None of the facilities being considered at the alternative sites are vulnerable to external events or natural phenomenon that are within their design basis. Moreover, even for external events or natural phenomenon that exceed the design basis (a low probability event), the onset of facility damage is typically insufficient to breach the AT-400A shipping containers. Of the natural phenomena capable of causing significant facility damage (if the design basis is sufficiently exceeded), earthquakes are the most likely to cause a significant release (relative to other natural phenomena). For this reason, earthquakes are the risk dominant natural phenomena at the alternative sites.
Preliminary test results demonstrate that an AT-400A shipping container can survive the impact of a half ton mass dropped from a height of 110 feet without any loss of containment capability (PC 1995). Thus, even if the external event or natural phenomenon induced facility damage is severe, there is a high probability that the containers will remain intact. In the context of Figure D.3.2-7, the frequency of a plutonium release is well into the not reasonably foreseeable range defined in section D.3.1. Although the consequences of a plutonium release initiated by an external event or natural phenomenon are potentially high, the relative risk from such scenarios is negligible because of the low frequency that the release can occur.
D.4 EVALUATION OF RISK-DOMINANT SCENARIOS
Both high frequency, low consequence scenarios (such as those occurring during normal operations), and low frequency scenarios having potentially high consequences (i.e., scenarios initiated by natural phenomena or external hazards), are included in Table D.3.2-1. These scenarios were left when the methodology discussed in section D.3 was applied to the Pantex Plant scenarios of Table D.3.2-2. For all scenarios, the frequency and consequence assessments were performed on a site-wide, rather than a facility-specific, basis. This means, for example, that the frequency of a hazardous material release involving a specific handling operation was estimated by first quantifying the probability, per handling operation, that the accident occurs and then multiplying that probability by the total number of handling operations performed annually on site. If the particular handling operation (e.g., involving weapon disassembly) is performed in several separate facilities, then the release frequency incorporates the contribution from all of the individual handling facilities. However, since handling operations typically involve only a single hazardous material unit at a time (e.g., just one pit or one tritium reservoir), the consequences were generally quantified using the release from a single, standard unit in an intact facility (unless the scenario involved an HE explosion).
Aircraft accidents (the risk dominant external hazard for all sites) were modeled somewhat differently. Due to the proximity of Zones 4 and Zone12 to established flight paths and their high inventory of radionuclides, the site-wide risk from aircraft accidents at Pantex Plant is governed by these zones. The material at risk from an aircraft accident is the inventory of the facility damaged by the impact. This differs from the consequences of most handling accidents (without an HE detonation) in that, in an aircraft accident, multiple units are involved and the facility can be extensively damaged. For alternative storage sites, the material at risk from an aircraft accident includes the inventory of the alternative pit storage facility.
Earthquakes are the risk dominant natural phenomena for all sites. All of the facilities that contain potentially risk significant quantities of hazardous materials were examined in the Pantex Plant seismic assessment. A unique aspect of this seismic assessment is that all site facilities would be simultaneously subjected to seismic stresses, given that an earthquake occurs. Hence, unlike handling and aircraft accidents, seismic events are truly site-wide and can result in releases from multiple facilities. For alternative storage sites, the material at risk from an earthquake is the inventory of the alternative pit storage facility.
D.4.1 Frequency Assessment
Quantifying the frequencies of risk-dominant scenarios required three distinct types of assessments addressing:
- Internal initiators.
- Aircraft accidents.
- Earthquakes.
The frequency assessment of internal initiators relied almost exclusively on published site-specific, accident-specific safety analyses (see references cited in volume I, section 4.14.2.1 and individual scenario descriptions). The basic methodology equated the scenario frequency to the frequency that an operation is performed (e.g., 2,000 disassemblies per year), multiplied by the probability that an operational error would result in a hazardous material release (e.g., the probability, per disassembly, that an operational error would cause a tritium or plutonium release).
For example, the explosive-driven plutonium dispersal from an internal event (Scenario 1) could result from operations conducted in bays, cells, and special purpose facilities. The probability (per operation) that an operational error would cause an explosive-driven plutonium release was estimated for each facility using data from available safety analyses. The frequency (per year) was quantified by multiplying the probability (per operation) by the annual number of operations in each facility, and then summing the results.
Appendix E describes the methodology used for assessing the frequency of aircraft accidents.
The frequency of hazardous material releases initiated by earthquakes is predicated upon a methodology developed in the DOE Standard for Natural Phenomena Hazards Design and Evaluation Criteria for Department of Energy Facilities (DOE 1994:C-8, C-9, C-25). Conceptually, the earthquake assessment methodology considers two parameters:
- Frequency, per year, that earthquakes of different intensities occur.
- Probability of facility failure (e.g., building collapse) given an earthquake with a particular intensity.
For a given earthquake intensity, the product of the earthquake frequency and facility failure probability is the frequency, per year, that earthquakes with the specified intensity would cause the facility to fail. By summing these products over the entire range of earthquake intensities, an overall frequency for earthquake induced facility failure is obtained. This basic methodology was directly applicable to earthquakes at the alternative storage sites.
Multiple facilities are at risk from earthquakes at Pantex Plant. For the Pantex Plant assessment, it was necessary to multiply the earthquake frequency by the probability that just one, two, or a specified number of facilities fail in order to determine the frequency, per year, that earthquakes with the specified intensity would cause various combinations of facilities to fail. For a given combination of facility failures, summing these products over the entire range of earthquake intensities gave the overall frequency for earthquake induced facility failures. Considering the overall frequency of multiple facility failures was necessary to quantify the total risk from earthquakes, which threaten all of the facilities onsite.
Facility failure would not necessarily result in a hazardous material release (e.g., it is extremely difficult for a facility failure to breach a shipping container). Using a methodology similar to the one applied for internal initiators, the scenario frequency was determined by multiplying the facility failure frequency (due to an earthquake) by the probability the failure would result in a hazardous material release. For Scenario 7 in Table D.3.2-1, the scenario frequency was determined by multiplying the facility failure frequency (due to an earthquake) by the probability that the failure would result in a fire that would damage the 12-42 South Vault tritium reservoirs.
D.4.2 Radiological Consequence Assessment
Two computer codes were used to assess the consequences of a radionuclide release:
- Melcor Accident Consequence Code System (MACCS)(NRC 1990a, NRC 1990b, NRC 1990).
- Explosive Release Atmospheric Dispersion (ERAD) (DOE 1992).
ERAD was used to quantify the consequences from scenarios in which the radionuclides are dispersed into the atmosphere explosively (i.e., by an HE detonation). All other scenarios involving a radionuclide release were quantified with MACCS. Descriptions of both codes follow.
D.4.2.1 Application of the Melcor Accident Consequence Code System
The MACCS computer code models the offsite consequences of an accident that releases a plume of radioactive materials to the atmosphere (NRC 1990a; NRC 1990b; NRC 1990). Should such an accidental release occur, the radioactive gases and aerosols in the plume would be transported by the prevailing wind while dispersing in the atmosphere. The environment would be contaminated by radioactive materials deposited from the plume and the population would be exposed to radiation. The MACCS calculation estimates the range and probability of the health effects induced by radiation exposures (that are not avoided by protective actions). There are two fundamental aspects of the organization of MACCS which are basic to its understanding: the time scale after the accident is divided into various "phases" and the region surrounding the site is divided into a polar-coordinate grid.
The time scale after the accident is divided into three phases: emergency phase, intermediate phase, and long-term phase. The emergency phase begins immediately after the accident and could last up to 7 days following the accident. In this period, the exposure of population to both radioactive clouds and contaminated ground is modeled. Various protective measures can be specified for this phase, including evacuation, sheltering, and dose-dependent relocation.
The intermediate phase is used to represent a period in which evaluations are performed and decisions are made regarding the type of protective actions that need to be taken. In this period, the radioactive clouds are assumed to be gone and the only exposure pathways are those from the contaminated ground. The protective measure which can be taken during this period is temporary relocation.
The long-term phase represents all time subsequent to the intermediate phase. The only exposure pathways considered here are those resulting from the contaminated ground. A variety of protective measures can be taken in the long-term phase in order to reduce doses to acceptable levels: decontamination, interdiction, and condemnation of property.
The spatial grid used to represent the region is centered on the facility itself. The user specifies the number of radial divisions as well as their endpoint distances. Up to 35 of these divisions may be defined, extending out to a maximum distance of 9,999 kilometers (6,200 miles). The angular divisions used to define the spatial grid correspond to the 16 directions of the compass.
The emergency phase calculations use dose-response models for early fatality and early injury and are performed on a finer grid than the calculations of the intermediate and long-term phases. For this phase, the 16 compass sectors are divided into 3, 5, or 7 user-specified subdivisions in the calculations.
For the analysis of high consequence accidents at the different facilities, the MACCS calculations used the source term data and modeled the dispersion and deposition of radionuclides released from facilities to the atmosphere with a straight-line Gaussian plume. Plume rise and dry and wet deposition were taken into consideration. One year of hourly onsite meteorological data and a weather bin sampling technique were used to represent the dispersion process according to each site's characteristic weather. Downwind concentrations of radionuclides up to a distance of 80 kilometers (50 miles) were calculated for each of 16 directional sectors around the facility.
Radiation doses to an offsite population were calculated in the dosimetry models using the concentrations of radionuclides obtained from the dispersion models. Exposure pathways considered in MACCS for calculating doses received during the period following an accident were direct radiation from the passing plume and from radioactive material deposited on the ground, inhalation from the plume, deposition on skin, and inhalation of resuspended ground contamination. Long-term exposure pathways and liquid exposure pathways were not considered. No credit was taken for short-term actions such as evacuation, sheltering, and relocation.
Resuspension of particulate matter that has settled out of the plume is explicitly modeled in MACCS. The inhalation dose of the emergency phase from the resuspended radionuclides after passage of a plume segment is calculated for each of the fine spatial elements using the following equation:
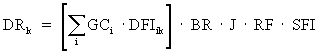
(Eq. D-6)
where:
DRk = Resuspension inhalation dose (Sv) to organ "k" after passage of a plume segment over a fine spatial element.
GCi = ground concentration (Bq/m2) of radionuclide "i" under the plume center line at the time that plume leaves the fine spatial element, calculated by the ATMOS module.
DFIik = inhalation dose conversion factor (Sv/Bq inhaled) to organ "k" for radionuclide "i", MACCS Dose Conversion Factors File.
BR = breathing rate (m3/s), user-specified.
J = off-center line correction factor (dimensionless), of the fine spatial element.
RF = time-integrated resuspension factor (s/m) defined below.
SFI = inhalation shielding factor (dimensionless), specified by user.
The resuspension factor, RF, is calculated using the following equation:
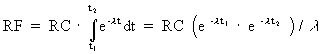
(Eq. D-7)
where:
RC = the resuspension coefficient that relates ground concentration to air concentration (m-1); user-specified.
l = the natural log of 2 divided by the resuspension half-life (s-1); user-specified.
t1 = the time from plume departure to the entrance of the individual into the spatial element(s).
t2 = the time from plume departure to the departure of the individual from the spatial element (s).
In addition, the chronic exposure model calculates doses from inhalation of resuspended radionuclides. These doses are calculated for all inhabitants living in areas that are not permanently interdicted.
The resuspension inhalation dose of the intermediate or long-term phase for a given time period is calculated for each of the coarse spatial elements using the following equation:
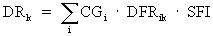
(Eq. D-8)
where:
DRk = resuspension inhalation dose (Sv) to organ "k" in a spatial element for a given time period.
GCi = Initial ground concentration (Bq/m2) of radionuclide "i" in a spatial element.
DFRik = resuspension inhalation dose factor (Sv-m2/Eq) to organ "k" for radionuclide "i" for a given time period, defined below.
SFI = inhalation shielding factor (dimensionless).
For the intermediate and long-term phases, the inhalation shielding factor for normal activity (user-specified) is used in the resuspension inhalation dose calculation.
The computation of the resuspension dose factor, DFRik, for a specific time period t1 to t2 requires the evaluation of the following function:
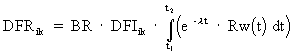
(Eq. D-9)
where:
DFIik = inhalation dose conversion factor (Sv/Bq inhaled) of either acute or lifetime dose to organ "k" for radionuclide "i", MACCS Dose Conversion Factors File.
BR = breathing rate (m3/s).
li = decay constant (s-1) of radionuclide i.
Rw(t) = resuspension weathering function, defined below.
If a radionuclide decays to a radioactive daughter, the resuspension inhalation dose resulting from the daughter is added to the resuspension inhalation dose of the parent radionuclide.
The resuspension weathering equation is a multi-term exponential decay function
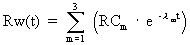
(Eq. D-10)
where:RCm = resuspension weathering coefficient (m-1) for the m-th term
lm = resuspension weathering decay constant (s-1) for the m-th term
D.4.2.2 Application of the Explosive Release Atmospheric Dispersion Computer Code
The ERAD code was developed by Sandia National Laboratories (DOE 1992). ERAD provides a three-dimensional numerical simulation for the dispersal of gaseous and particulate airborne source materials in which initial cloud dynamics, turbulent diffusion, and buoyancy effects coupled with elevation-dependent physical and thermodynamic properties of the plume are considered. ERAD's meteorological component implements state-of-the-art scaling derived from Monin-Obukhov similarity theory to model turbulent velocity profiles in the planetary boundary layer. Particle dispersion and depletion are modeled as stochastic processes and simulated using a discrete-time Lagrangian Monte Carlo algorithm. Several thousand individual particle trajectories are traced to determine respirable dosage and deposition contours over the affected area. Particulate resuspension is not modeled in ERAD.
ERAD was developed to give real-time predictions, using field-portable computers, of the radiological hazards resulting from accidents arising in the storage and transportation of nuclear materials and possible acts of terrorism. Actual meteorological data are input to ERAD to model surface friction, thermal turbulence, and mixing height of the planetary boundary layer. These parameters include:
- Effective surface roughness length.
- Relative humidity and atmospheric pressure.
- Vertical profiles of atmospheric temperature, wind direction, and speed.
The menu-driven code has an extensive health physics library that allows the user to select specific radionuclides. Downwind consequences of different types of atmospheric releases of radioactive materials may be analyzed by three programs:
- Non-buoyant-continuous or puff releases.
- Detonation-releases resulting from the detonation of chemical high explosive.
- Fire Plume-continuous releases resulting from fuel fires.
The fire plume model for the ERAD code is currently undergoing verification and was not used for calculations in this EIS.
The complete ERAD code with UNIX-based graphical user interface was developed for Sun workstations. Depending on the speed of the machine, a 10,000-particle Monte Carlo simulation may take as long as 5 to 10 minutes to execute (5,000-particle simulations are usually adequate in most cases).
Health effects consequences for an accident under these circumstances are obtained by multiplying the predicted dosages or time-integrated concentrations by the proper scaling factors. Health risk to the exposed population may be determined by summing the individual health effects over the number of people residing in the affected area.
Perhaps the most notable feature of the ERAD result is the asymmetrical distribution of the dosage contours about the mean surface wind direction. The effect is caused by the variation of wind direction with altitude, relative to surface winds. ERAD also accounts for terrain effects through a term for effective roughness length. Mechanical turbulence increases with the roughness length due to increased surface friction. This decreases the area enclosed by a given dosage isopleth because of enhanced mixing of airborne materials with entrained air.
Two consequence assessments, representative and upper bound, are performed for each scenario that releases radionuclides. The representative consequence represents what is most likely to occur if the release is initiated, while the upper bound indicates sensitivity to uncertainties in the release source term, facility response, and meteorology. For MACCS calculations, the representative consequences cited in Tables D.4.2.2-1 and D.4.2.2-2 are estimated by Monte Carlo simulation. This is achieved because MACCS calculates the consequences for numerous meteorological conditions and then identifies the mean and upper bound consequences.
Table D.4.2.2-3Representative Source Terms
ERAD lacks the Monte Carlo capabilities of MACCS. For ERAD calculations, the typical consequences cited in Tables D.4.2.2-1 and D.4.2.2-2 use mean meteorological parameters obtained from upper air soundings recorded at the Amarillo International Airport. Upper bound consequences obtained from ERAD are for upper bound meteorological conditions being used in developing Pantex Plant safety documents.
For example, the consequence of Scenario 1 is the arithmetic mean for the consequences associated with explosive driven plutonium releases from internal events in bays, cells, and special purpose facilities. This involved three sets of calculations. First, consequences were calculated for the case in which Scenario 1 occurs in a bay. Next, consequences were calculated for the case in which Scenario 1 occurs in a cell. Finally, consequences (both the exposure and excess fatal cancers) were calculated for the case in which Scenario 1 occurs in a special purpose facility.
The arithmetic mean of these consequences is the probability that Scenario 1 occurs in a bay, multiplied by the consequences of the case in which Scenario 1 occurs in a bay; plus the probability that Scenario 1 occurs in a cell, multiplied by the consequences for the case in which Scenario 1 occurs in a cell; plus the probability that Scenario 1 occurs in a special purpose facility, multiplied by the consequences for the case in which Scenario 1 occurs in a special purpose facility. The probability used for each facility was the ratio of the frequency (i.e., the probability per operation that an error causes a release from the facility, multiplied by the annual number of operations in the facility) that Scenario 1 occurs in the facility, divided by the frequency of Scenario 1 (i.e., 1.1 x 10-5 per year.)
Tables D.4.2.2-1 and D.4.2.2-2 give the representative and upper bound consequences for each risk dominant scenario that involves a radionuclide release. Table D.4.2.2-3 gives the source terms (i.e., curies of respirable plutonium and tritium released to the atmosphere as a result of a potential accident) used to quantify the representative public and non-involved worker consequences in Tables D.4.2.2-1 and D.4.2.2-2. The source term used for a handling accident at an alternative site is 9.2 x 10-5 curies of plutouium.
Table D.4.2.2-4 gives the representative upper bound consequences to the maximally exposed offsite individual for each risk dominant scenario that involves a radionuclide release. This hypothetical individual is located at the site boundary closest to the radiological release. The wind is assumed to blow the radiological release directly towards this individual. For scenarios such as Scenario 1 in which more than one facility has been modeled, results for the facility giving the highest consequence at the site boundary are presented in Table D.4.2.2-4.
The fatal cancer consequences presented in Table D.4.2.2-1 are the excess fatal cancers expected to occur over a 50-year period following the accident in the population in the Region of Influence (ROI). For Pantex Plant, the population in the ROI is 267,107 people. As stated previously, 20 percent of this population is expected to succumb to fatal cancer from all other causes (0.2 x 267,107 = 5.3 x 104 fatal cancers). For the fatal cancer consequences presented in Table D.4.2.2-2, the non-involved worker is defined as a receptor 100 meters (328 feet) downwind from the release point, along the plume center line.
Table D.3.2-1 identifies Scenarios 1 and 3 as involving radionuclide releases associated with HE explosions. In Scenario 1, the HE explosion is initiated during normal operations. A seismic event or aircraft accident initiates the HE explosion considered in Scenario 3.
Sensitivity studies using ERAD disclose that the consequences of scenarios involving HE explosions vary with the ratio of plutonium to HE. In assessing the consequences presented in Tables D.4.2.2-1 and D.4.2.2-2, the ratio of plutonium to HE was varied to determine the maximum consequences to the public.
The impacts of accidents presented are meant to bound the consequences that would occur in the unlikely event of a serious accident at Pantex Plant. For example, the upper bound dose to the maximally exposed offsite individual (MEOI) from the bay explosion event within Scenario 1 varies significantly based on the high explosive charge to plutonium mass ratio of specific weapon systems that could be present in bays. When the upper bound MEOI dose is calculated for differing charge to mass ratios, the MEOI dose varies from 6 rem to approximately 100 rem (DOE 1996i). The upper bound dose numbers for the MEOI presented in Table D.4.2.2-4 are based on the worst case weapon system for MEOI exposures and as such bound the consequence from an accident involving the majority of weapons systems that could be present within the bays.
The representative consequences cited in Tables D.4.2.2-1 and D.4.2.2-2 were used for scenario screening and estimating risk. These typical values are utilized because they correspond to a greater level of human health risk than the upper bound values (which are included to indicate uncertainty levels). Except for Scenario 3, the representative and upper bound consequence assessments in Tables D.4.2.2-1 and D.4.2.2-2 rely on the MACCS software described in section D.2.1.2. Based on the Monte Carlo sampling used in MACCS, the probability of a potential accident scenario actually producing consequences equal to or exceeding the upper bound value is less than 0.05 (i.e., one chance in twenty). Thus, the frequency of an accident corresponding to the upper bound consequences is about a factor of 20 below the expected accident frequency.
Consider the first Pantex Plant scenario in Table D.4.2.2-1. If l1 denotes its expected frequency and RT,1 represents its representative risk, then:
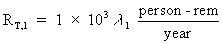
(Eq. D-11)
However, the risk associated with the upper bound value, RU,1, is:
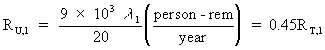
(Eq. D-12)
This same conclusion applies to the other scenarios whose consequence assessments rely on MACCS.
The consequence assessment for Scenario 3 at Pantex uses ERAD calculations exclusively. A conservative estimate is that there is less than a 5 percent chance that Scenario 3 would produce consequences that exceed the upper bound values. If l3 denotes the expected frequency of Scenario 3 and RT,3 represents its typical risk, then:
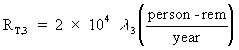
(Eq. D-13)
However, the risk associated with the upper bound value, RU,3, is
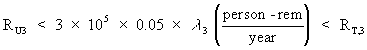
(Eq. D-14)
Here again, the upper bound risk is less than the representative risk impact on human health. The single exception in Table D.4.2.2-1 is for Scenario 3 Configuration 2 at Pantex. Using the actual exposure estimates (4.4 x 103person-rem [representative] and 8.9 x 104 person-rem [upper bound]), the upper bound risk may exceed the typical risk by approximately 1 percent.
Direct comparisons between the scenarios assessed for the alternative sites and Pantex Plant can be misleading. Although Scenario 6 at Pantex Plant includes a pit breach initiated by a forklift accident, the risk from this scenario is dominated by handling accidents in bays and special purpose facilities. Thus, a number of different events contribute to the risk and consequences from Scenario 6 at Pantex Plant, as opposed to the single event (i.e., forklift accident) that dominates the risk at the alternative sites.
D.5 EVALUATION OF THE RISK FROM NORMAL OPERATIONS
Human health impacts from hazardous chemicals are only a concern at Pantex Plant, since relocating pit storage does not alter the human health impacts from hazardous chemicals at the receiving sites. Air quality analyses using the Industrial Source Complex Short-Term (ISCST2) Model quantified the air concentrations of chemical releases during normal operations (EPA 1987a; EPA 1987). These concentrations were evaluated for all chemicals considered to be carcinogenic and having associated risk factors. Using the chemical concentration results and the risk factors, an estimate of the cancer risk to workers and a qualitative evaluation of public risk was determined.
Toxic, noncarcinogenic chemicals were evaluated for offsite effects using a hazard index, as shown in volume I, chapter 4, Table 4.14.1.2-2. Chemical concentrations onsite were compared to published threshold limit values for chemical substances to determine the extent of potential human health impacts. None of the threshold limit values are exceeded onsite.
Radiation exposure during normal operations is dominated by external exposure to radiation workers. To quantify changes in worker exposure for different disassembly and assembly rates, As Low As Reasonably Achievable goals were used to estimate an average exposure per operation (PC 1994). This average exposure was then multiplied by the number of operations per year.
Radiation exposure to the public is predominantly from air emissions. The majority of these radiological air emissions are the result of off gassing from Cell 1 and not from normal operations. However, environmental monitoring data establish that these radiological air emissions contribute approximately a factor of one in a billion to the annual radiation dose to an average individual in the vicinity of Pantex Plant.
D.6 UNCERTAINTIES
The sequence of analyses performed to generate the radiological impact estimates from normal operation and facility accidents include: (1) selection of normal operational modes and accident sequences, (2) estimation of source terms, (3) estimation of environmental transport and uptake of radionuclides, (4) calculation of radiation doses to exposed individuals, and (5) estimation of health effects. There are uncertainties associated with each of these steps. Uncertainties exist in the way the physical systems being analyzed are represented by computational models and in the data required to exercise the models (due to measurement errors, sampling errors, or natural variability).
In principle, one can estimate the uncertainty associated with each source and predict the remaining uncertainty in the results of each set of calculations. Thus, one can propagate the uncertainties from one set of calculations to the next and estimate the uncertainties in the final results. However, conducting such a full-scale quantitative uncertainty analysis is neither practical nor a standard practice for a study of this type. Instead, the analysis is designed to ensure-through judicious selection of release scenarios, models, and parameters-that the results represent the potential risks.
This is accomplished by making assumptions in the calculations at each step. The models, parameters, and release scenarios used in calculations are selected in such a way that most intermediate results and consequently, the final estimates of impacts are greater than what would be expected. As a result, even though the range of uncertainty in a quantity might be large, the value calculated for the quantity is close to one of the extremes in the range of possible values, so that the chance of the actual quantity being greater than the calculated value is low (or the chance of the quantity being less than the calculated value if the criteria are such that the quantity has to be maximized). This has been the goal of the radiological assessment for normal operation and facility accidents in this study (i.e., to produce results that are conservative).
The degree of conservatism in the calculated results is closely related to the range of possible values the quantity can have. This range is determined by what can be expected to realistically occur. Thus, the only processes, events, and accidents considered are those credible for the conditions under which the physical system being modeled operates. This consideration has also been employed for both normal operation and facility accident analyses.
REFERENCES
| DH 1993 | San Diego County Department of Health Services, Hazardous Materials Management Division Risk Management and Prevention Program Requirements and Guidelines, August 1993. |
| DOD 1977 | DOD, System Safety Program Requirements, MIL-STD-882B, prepared by the U.S. Department of Defense, June 1977. |
| DOE 1992 | DOE, Description and Validation of ERAD: An Atmospheric Dispersion Model for High Explosive Detonations, SAND92-2069, prepared by Sandia National Laboratories, for the U.S. Department of Energy, Albuquerque, NM, October 1992. |
| DOE 1992a | DOE, Final Safety Analysis Report Pantex Plant Zone 4 Staging and Interim Storage for Nuclear Weapons and Components, Pantex Plant, Amarillo, TX, December 1992. |
| DOE 1994 | DOE, DOE Standard, Natural Phenomena Hazards Design and Evaluation Criteria for Department of Energy Facilities, prepared under Contract Number DOE-STD-1020-94 by the U.S. Department of Energy, April 1994. |
| EPA 1987 | EPA, Industrial Source Complex (ISC) Dispersion Model UserĂs Guide, Volume 2, Second Edition, Revised, EPA-450/4-88.002b, prepared by the U.S. Environmental Protection Agency, Office of Air Quality Planning and Standards, Research Triangle Park, NC, December 1987. |
| EPA 1987a | EPA, Industrial Source Complex (ISC) Dispersion Model UserĂs Guide, Volume 1, Second Edition, Revised, EPA-450/4-88.002a, prepared by the U.S. Environmental Protection Agency, Office of Air Quality Planning and Standards, Research Triangle Park, NC, December 1987. |
| Jones 1988 | Jones, J.V., Engineering Design Reliability, Maintainability, and Testability, TAB Books, Inc., Blue Ridge Summit, PA, 1988. |
| NAP 1990 | Health Effects of Exposures to Low Levels of Ionizing Radiation BEIR V, National Academy Press, Washington, D.C. 1990. |
| NRC 1990 | U.S. Nuclear Regulatory Commission, Quality Assurance and Verification of the MACCS Code, Version 1.5, NUREG/CR-5376, prepared by Idaho National Engineering Laboratory, Idaho Falls, ID, February 1990. |
| NRC 1990a | U.S. Nuclear Regulatory Commission, MELCOR Accident Consequence Code System (MACCS) UserĂs Guide, Volume 1, NUREG/CR-4691, prepared by Sandia National Laboratories, Albuquerque, NM, February 1990. |
| NRC 1990b | U.S. Nuclear Regulatory Commission, MELCOR Accident Consequence Code System (MACCS) UserĂs Guide, Volume 2, NUREG/CR-4691, prepared by Sandia National Laboratories, Albuquerque, NM, February 1990. |
| PC 1994 | Cole, D.J., ˘1995 ALARA Goals÷, Memo from D.J. Cole to W.A. Weinreich, Mason & Hanger-Silas Mason Company, Inc., December 21, 1994. |
| PC 1995 | Baca, W., ˘AT-400A Testing÷, Telecon from Wendy Baca, DOE Albuquerque Operations Office, Nuclear Explosive Safety Division, to Bret Simpkins, Tetra Tech, Inc., Albuquerque, NM, March 20, 1996. |
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|






