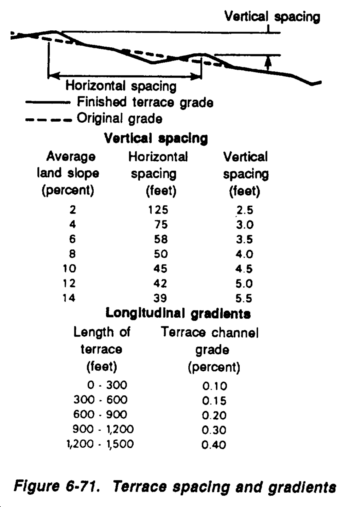
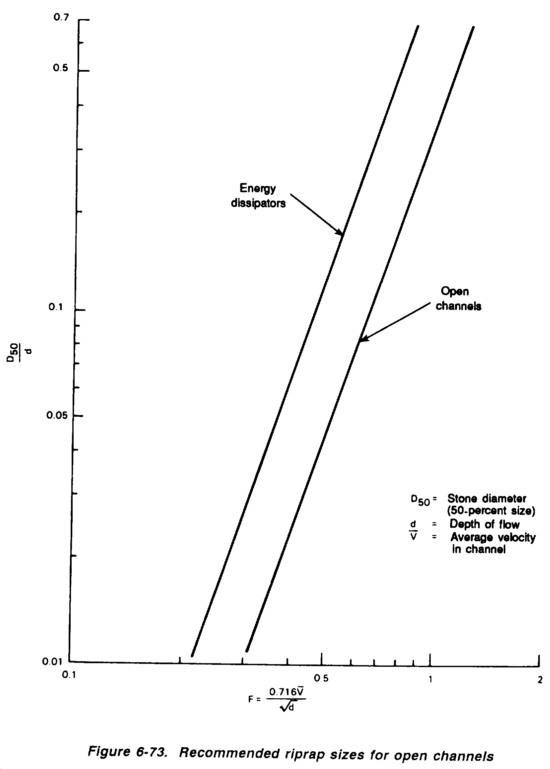
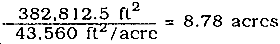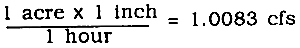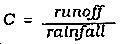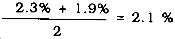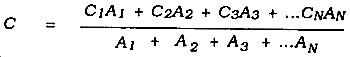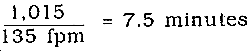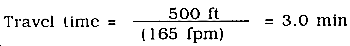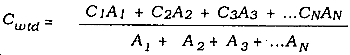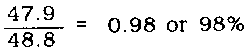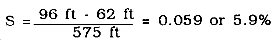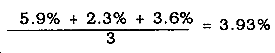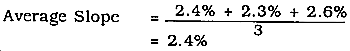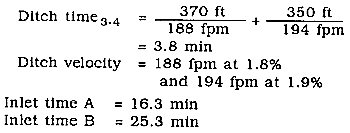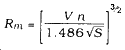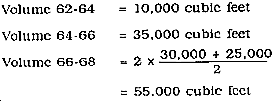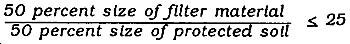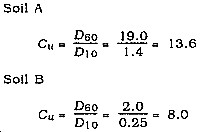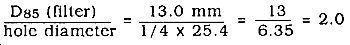CHAPTER 6
DRAINAGE
Inadequate drainage is the most common cause of road and airfield failure. Therefore, drainage is a vital consideration in planning, designing, and building military roads and airfields. It is important during both construction and use.
SECTION I. CONSTRUCTION DRAINAGE
Commanders and construction supervisors must ensure continuous maintenance of the drainage system during construction of a military road or airfield. The construction drainage system is temporarily established to prevent construction delays and structural failure before completion. Generally, long delays will result if drainage is not continuously emphasized by the command. Construction drainage must be completed before needed; when a storm begins it is too late to start drainage work. Construction-drainage measures used during different phases of construction are discussed below.
PRELIMINARY MEASURES
RECONNAISSANCE
Prior to the start of construction, preliminary reconnaissance of an area should disclose features that require advance drainage planning and operations. These features include--
- Springs and seepage on hillsides which may indicate perched or high water tables detrimental to cuts.
- Trees adjacent to dry or low-flow streams that could receive their root water from a groundwater table flowing near the surface. Compacted fills across such areas could change the movement of the flow.
- Vegetation or cover that, if removed during the clearing and grubbing phase of construction, could increase surface runoff.
- The presence of level areas which have good vegetation and adjacent slopes. These areas may indicate a shallow groundwater table with capillary water movement and may require intercepting subsurface drainage.
- Streams that should be checked for normal high-water and flood indicators.
PROTECTIVE MEASURES
Controlling runoff during construction can be costly. The following measures can help maintain satisfactory drainage during construction:
- Make maximum use of existing ditches and drainage features. Where possible, grade down hill to allow economical grading and to take advantage of natural drainage.
- Use temporary ditches to help construction drainage. Ensure efforts are made to drain pavement subgrade excavations and base courses to prevent detrimental saturation. Carefully consider the drainage of all construction roads, equipment areas, borrow pits, and waste areas.
- Be aware of areas where open excavation can lead to excessive erosion. The discharge of turbid water to local streams will require temporary retention structures.
- Hold random excavation to a minimum, and sod or seed finished surfaces immediately.
- Plan timely installation of final storm-drain facilities and backfilling operations to allow maximum use during construction.
AREA CLEARING
The following constraints should be considered:
Existing Drainage
Clear excess vegetation from streams. This increases the velocity and quantity of flow. Widening the stream can also increase the flow. Bends and meanders can be cut to straighten the stream. Use care in making major alignment changes because they can change the hydraulic characteristics of the stream. This change could adversely affect other parts of the stream.
Vegetation Removal
Military projects may require the removal of all vegetation from large areas. Consider the following factors with regard to construction stripping:
- Select a disposal area that will not interfere with or divert the drainage pattern of surface runoff. If the drainage pattern is disturbed, the stripped material may form a barrier resulting in pending and may otherwise affect adjacent areas.
- Be aware that removing the vegetation from an area can lead to excessive surface runoff and erosion. This could lead, in turn, to silting of channels and flooding of low areas.
- Consider that serious bank erosion due to surface runoff may occur if vegetation adjacent to the banks of streams or ditches is removed. To avoid this, it may be necessary to leave the vegetation or to provide a berm with a chute.
- In large, cleared areas, control runoff sediments to prevent failure of other structures and possible adverse environmental effects. This is more of a concern in permanent construction than in wartime TO construction.
Clearing, Grubbing, and Stripping
Any clearing, grubbing, and stripping must include filling holes and back dragging or grading to a slight slope. This will ensure proper runoff and prevent water from collecting and saturating the subgrade. If filling and grading is not done, the advent of rain will make it necessary to strip off any wet soil until dry soil is reached to start the fill. Some ditching may be required to direct the surface flow to an outlet point.
Fill
When placing fill, exercise firm control over the project to prevent adverse effects from improper drainage procedures. Some of the factors requiring attention are--
- The fill section must be rolled smooth at the end of each working day to seal the surface. No areas should be left that can hold standing water.
- The fill surface must be kept free of ruts caused by trucks and other equipment. These depressions collect rain and saturate the subgrade. Also, the surface must be crowned to discharge runoff quickly.
- When the fill area is large, it may be necessary to create swales (depressed areas) to conduct surface runoff to discharge outlets.
- To allow fill to proceed, it may be necessary to install temporary culverts in the fill area in places other than final design locations. After the fill area has reached design depth, the design culverts can be properly trenched in place.
Ditching
Use interception ditches during construction to collect and divert surface runoff before building the designed system. Prior to construction, conduct a site investigation of the general layout, consistent with the work plan. When interception ditches cannot be made part of the design drainage, consider removing the ditches by backfilling and compacting.
Locate interceptor ditches on hillsides and at the foot of slopes to intercept and divert runoff from the construction site. Make these ditches part of the final drainage system wherever possible. Roadside ditches, required during all construction stages, should be placed at design locations.
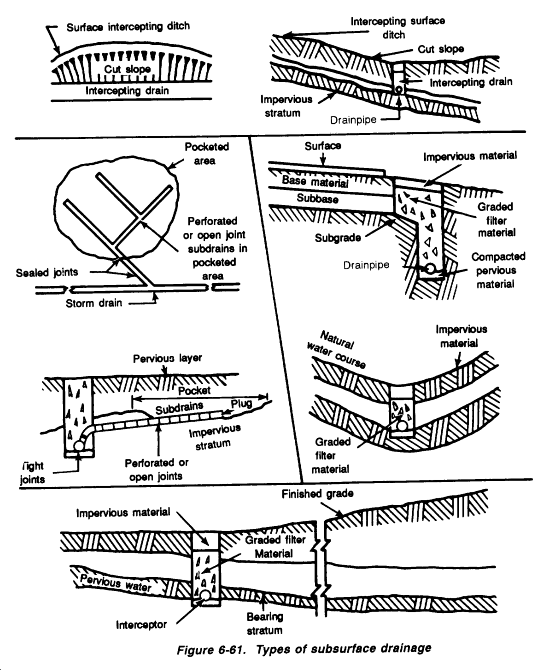
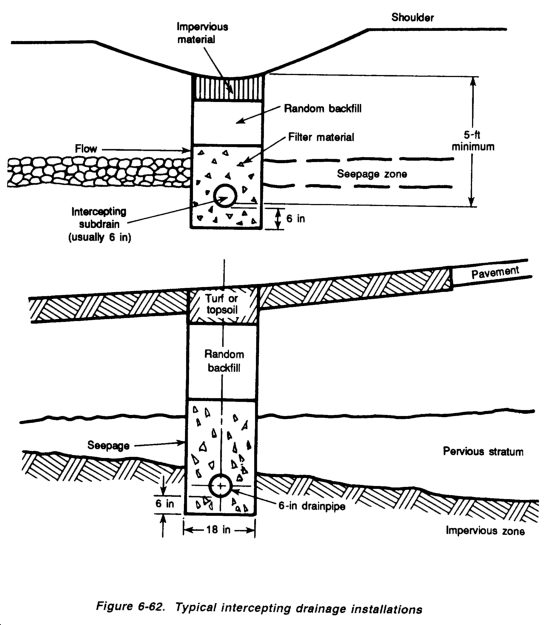
During construction, use deep ditches for subsurface drainage. They intercept groundwater flow, as shown in Figure 6-1. If groundwater flow must be intercepted but ditching is not possible, modify the ditch into a subsurface drainpipe system.
Ditching may be required in swamp areas to either continue drainage ditches to an outlet point or drain the area.
Engineers may use explosives in such cases, since the soil may not be capable of supporting construction equipment. Draglines should also be considered.
Timber or steel mats can be used to provide a firm foundation and support equipment during the operation.
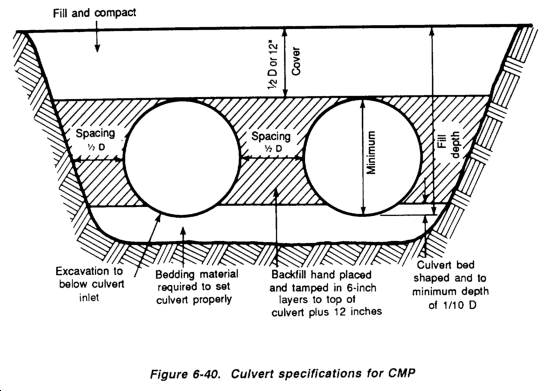
Culverts
Culverts are required during construction to allow surface runoff. If streams must be diverted to allow the construction of permanent culverts, use temporary culverts in the construction area. Never close natural drainage channels, even if they are currently dry. If these channels are closed, surface runoff from sudden storms could cause a serious problem. These conditions must be anticipated. Construction drainage must keep pace with the construction project.
DRAINAGE HYDROLOGY
The hydrologic cycle is the continuous process which carries water from the ocean to the atmosphere, to the land, and back to the sea. A number of different subcycles can take place concurrently in the overall cycle and are discussed below.
PRECIPITATION
Rainfall is the moisture-delivery mechanism of primary concern to most military drainage designers. Snowmelt may be of greater concern in colder climates or in the design of reservoirs in milder regions. These concerns are beyond the scope of this manual, but they are included in TM 5-852-7. The amount of rainfall that evaporates depends on the surface temperature of ground features, the air temperature, the wind speed, and the relative humidity. Evaporation occurs while rain is falling to the ground and after it lands on vegetation and other ground cover.
INTERCEPTION
Rainfall coming to rest on vegetation is said to have been intercepted. Large quantities of water can be trapped in the leaf canopy of trees and plants. Rain does not reach the soil until the holding capacity of the vegetation canopy is exceeded.
INFILTRATION
A significant portion of the water that actually strikes the soil soaks into the ground. This process is call infiltration. The rate of absorption and the quantity of water absorbed depends on the soil type, the vegetation, the terrain slope, and the soil moistness prior to the rain. Stormwater runoff begins to accumulate only when the rate of rainfall exceeds the rate of infiltration.
DETENTION
Before overland water flow can begin its downhill motion, it must be deep enough to overcome any obstacles to its movement. Detention is the amount of water required to fill depressions of any size in the earth's surface. Except by infiltration or evaporation, no water can leave a depression until the holding capacity of the depression has been exceeded.
TRANSPIRATION
On a long-term basis, vegetation returns water to the atmosphere through a process called transpiration. Because of the time involved, transpiration has no immediate effect on water runoff in an area.
RUNOFF
Evaporation, interception, infiltration, detention, and transpiration are all moisture losses. Runoff is precipitation minus these moisture losses.
STORMS
Storms can deliver a large quantity of water to the earth in a short period of time. For that reason, the study of storms is an important part of the study of drainage hydrology. This section discusses storms in terms of duration, frequency, and intensity. It describes procedures for determining maximum storms and introduces the subject of runoff.
Duration
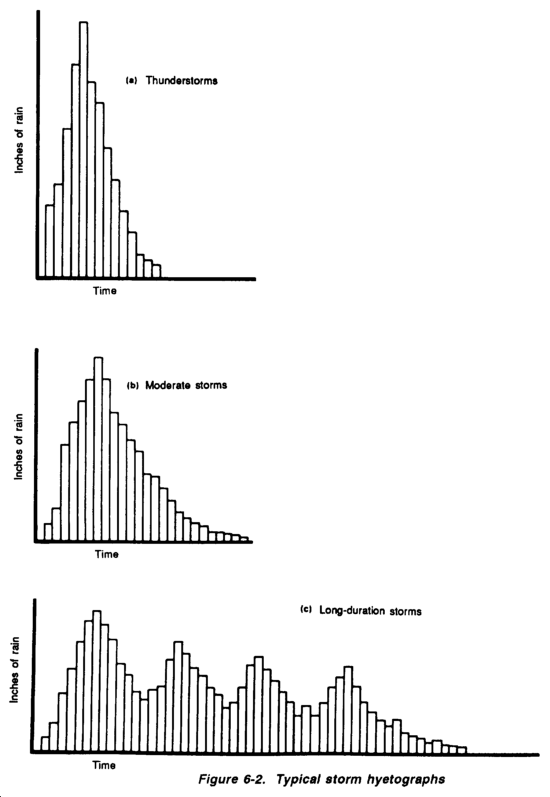
Duration is the length of time a storm lasts. After many years of observation, hydrologists have determined that a storm of long duration usually has low intensity. In contrast. a high-intensity storm usually has a short duration. Figure 6-2 shows typical storm hydrography developed by the National Weather Service. Time, usually measured in hours, is depicted horizontally. The amount of rain for each unit of time is measured vertically in inches. The total amount of precipitation is the area of the graph. The five main types of storms are described below.
Thunderstorms, represented by Figure 6-2(a), are local atmospheric disturbances of short duration and high average rate of rainfall (intensity). They are characterized by thunder, lightning, torrential rain, and sometimes hail. Thunderstorms tend to govern the design of drainage for small areas.
Moderate Storms
Moderate storms, represented by Figure 6-2(b), cover larger areas for several hours with moderate intensity. These storms develop greater total precipitation than thunderstorms. The moderate storm normally controls the design of drainage structures for medium-sized basins.
Long-Duration Storms
Long-duration storms, represented by Figure 6-2(c), often have several peaks of high rainfall. Durations may be up to several days, developing very large amounts of precipitation at relatively low average rates of rain fall. With a low average rate of rainfall, such storms have little or no impact on small-or medium-sized drainage basins, but they normally control the design of drainage structures for large basins.
Monsoons
Monsoons are seasonal winds of the Indian Ocean and southern Asia. These winds blow from the south during April to October and from the north during the rest of the year. Heavy rains usually characterize the April-to-October season. This rain is not normally continuous; it rises to a peak and then subsides in a cyclic fashion.
Tropical Cyclones
Hurricanes and typhoons are storms caused by severe cyclonic disturbances over a wide area. Precipitation is normally heavy and long.
Design Life Versus Actual Life of a Structure
The design storm is an idealized storm that is expected 10 be equalled or exceeded at least once during the design life of a drainage system. For example, if a drainage system has been designed for an estimated life of five years, then the design storm will have a five-year frequency. The frequency of a design storm is the average return period of a storm. For example, if a two-year frequency storm has an intensity of 1.5 inches of rainfall per hour, it can be expected that a storm of that intensity or greater will recur an average of once every two years. Two years is also called the return period. The reciprocal of the return period is the probability of having a storm of that value or greater in any one year.
For the two-year-frequency storm, the probability of having a storm equalling or exceeding the value in any one year is 0.5 (two out of four times).
The design-storm frequency for TO construction is normally two years. If construction with a longer estimated life is desired, the appropriate design storm should be specified in the authorizing directive.
As with any statistical method of describing essentially random, natural events such as weather, there is a degree of uncertainty. The two-year design storm occurs on the average every two years; it is not guaranteed to occur every two years. Statistically, the probability of a storm equal to or greater than the two-year design storm occurring in any two years is 0.75 (three out of four times). Details of the statistics involved can be found in hydrology textbooks.
WEATHER DATA
If there are extensive rainfall and rain-rate records for the location of interest, and if hydrologists have examined those records statistically to formulate intensity-duration tables, then those tables can be obtained through the Air Force staff weather officer. The staff weather officer is normally located at division level.
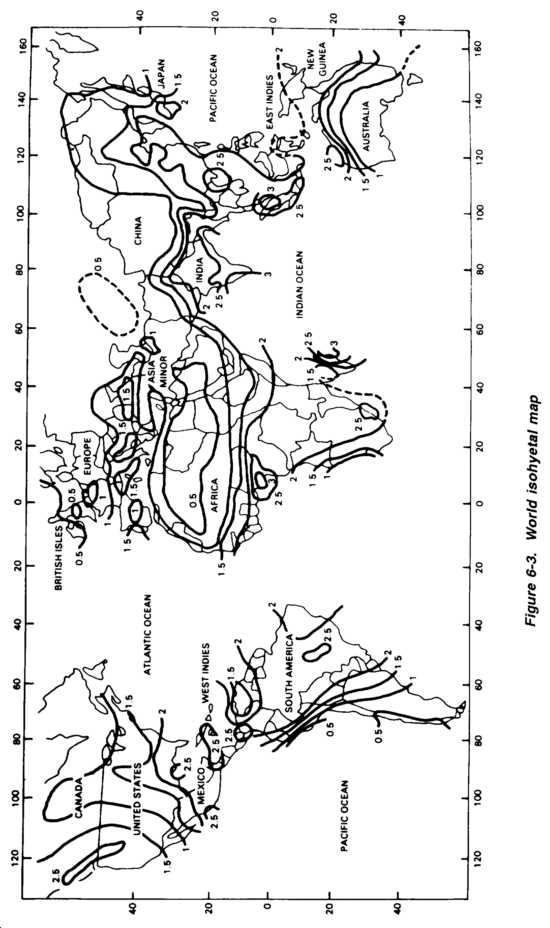
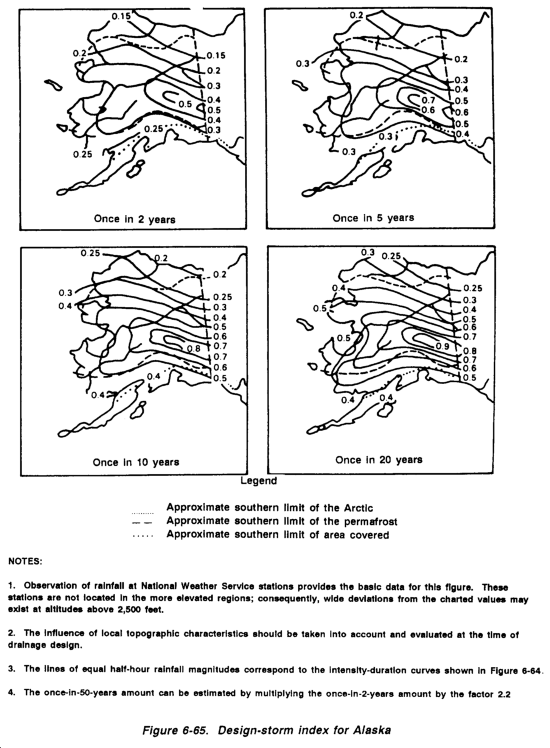
Within the United States, the data will generally come from the National Weather Service, either directly or through the Air Force. Overseas, the staff weather officer may be able to obtain data from local government sources, but it may take considerable time to obtain. However, it is unlikely that such pinpoint data is available in many overseas TO locations. When weather data is not available, use rainfall isohyetal maps. Isohyetal maps have contours of equal rainfall intensity just as topographic maps have contours of equal elevation. Figure 6-3 is an isohyetal map of the world, in this case showing the iso-intensity lines for a 60-minute, 2-year storm.
To properly read a value on the isohyetal map, find the project location and read the value of the appropriate isohyet(s).
Do not interpolate. If a project location falls--
- On an isohyetal line, read the value of that isohyet.
- Between two isohyets, read the larger value.
- Within an encircling isohyetal line, read the value of the encircling isohyet.
Examples (in inches per hour (in/hr)):
|
Southern Australia |
1.0 |
|
|
North Dakota |
1.5 |
|
|
Florida |
2.5 |
|
|
Washington, DC |
1.5 |
|
|
Vietnam |
2.5 |
|
|
Cuba |
2.5 |
|
|
New Orleans, Louisiana |
2.5 |
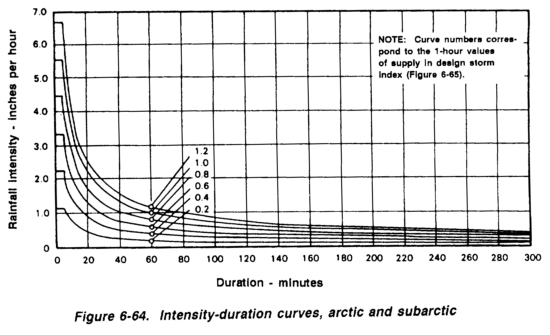
Note that the intensities just found are for a 60-minute storm. This must now be adjusted to the critical duration of the project under construction. Once the critical duration has been determined, make the adjustment using the standard rainfall intensity-duration curves in Figure 6-4.
The standard curves are numbered 1.0, 2.0, 3.0, and 4.0, with intermediate values readily interpolated. Note that curve number 1 passes through 1 inch per hour at 60 minutes, curve number 2 passes through 2 inches per hour at 60 minutes, and so on.
Where intensity is known for any nonarctic location (taken from the isohyetal map, Figure 6-3, and critical duration is calculated, the intensity (I) can easily be determined. (The standard intensity-duration curves are applicable to any frequency, not just a 2-year frequency.)
To use Figure 6-4, enter the graph using the Duration in Minutes (Tc). Follow the line vertically until it intersects the curve whose number corresponds to the 60-minute intensity determined from the isohyetal map (or from pinpoint data, if you choose not to draw your own intensity-duration curve). Read horizontally to the left to determine the rainfall intensity (I) in inches per hour. The following is an example:
|
I60, 2-yr |
Critical |
|
|
|
||
1.0 |
50 |
1.2 |
RUNOFF
Precipitation supplies water to the surface, but evaporation, interception, and infiltration begin to draw water at the start of the storm. Eventually, if the storm is strong enough, vegetation and other surface characteristics, such as depressions and soil, will become saturated, allowing water to flow freely over the surface. This condition is called runoff and is usually measured in cubic feet per second (cfs). Runoff begins sometime after the beginning of precipitation and may continue long after precipitation ends.
The total quantity of runoff from a given area, after it is collected in channels and streams, is the flow estimate used to design an area's drainage structures.
Transpiration and evaporation also draw from the water supplied by precipitation. However, these are relatively small losses and will not usually affect military drainage design. Estimating runoff will be discussed later in this chapter. Once the runoff has been determined, necessary ditches and culverts can be designed.
THE HYDROGRAPH
Stream-water flow may originate from surface runoff, groundwater, or both. Runoff reaches the stream as overland flow. Groundwater flow results from side-bank seepage and springs. The hydrography depicts the fluctuations of flow with regard to time.
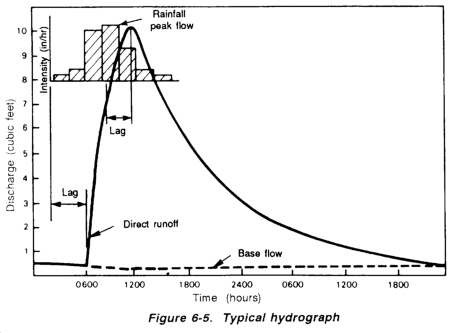
The elements of a hydrograph are base flow, lag time, peak flow, lime of concentration (TOC), and flow volume. Each stream will have its own characteristic hydrography with widely varying values for the elements. A typical stream-flow hydrography is shown in Figure 6-5.
BASE FLOW
The base flow of a stream depends upon the amount of groundwater that seeps into the stream and its tributaries from their banks and the flow from permanent springs and swamps. Depending on the area, climate, and groundwater level, it may flow at a fairly constant rate. Conversely, the flow may fluctuate widely or even cease completely for some periods of time.
LAG TIMES
When precipitation begins over an area, there is an initial period during which the loss factors induced by interception, infiltration, and detention take effect before any surface runoff takes place. Stream flow will increase only when these initial losses have been satisfied and surface runoff begins. This is known as initial lag time. The length of this lag time is influenced by vegetation and other terrain characteristics. For example, a grass-covered parking area will have a longer initial lag period than an asphalt parking lot of the same size. A second lag time occurs between the time the storm reaches its peak pecipitation rate and the time the stream reaches its maximum flow. The length of this secondary lag time is influenced by the size of the area drained. In small-and moderately sized drainage areas, there will be only slight differences between storm peak and stream peak.
PEAK FLOW
The peak of the hydrography is the maximum stream flow that will occur during a particular storm. In general, peak flow is generated when the entire drained area is discharging its runoff. Peak flow is read directly from the maximum ordinate of the hydrograph. This flow determines the size of the drainage structures required at the basin outlet.
TIME OF CONCENTRATION
The TOC is the time it lakes for an entire drainage basin to begin contributing runoff to the stream. Assuming uniform rainfall, the hydrography peaks at that point. TOC is critical to the drainage engineer, since it determines the duration of the storm that will demand the most from the drainage system; that is, the storm's critical duration.
VOLUME OF FLOW
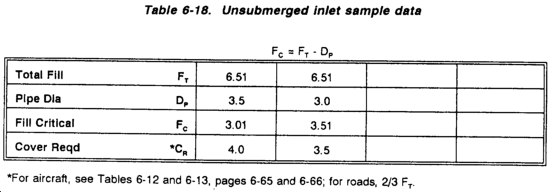
The area under the curve of the hydrography indicates the total flow, in cubic feet, resulting from any particular storm. It is used in drainage design for determining pending times when it is practical to use culverts with submerged inlets.
CONSTRUCTING A HYDROGRAPHY
A hydrograph is constructed by measuring a stream's rise and fall and the times related to these changes in flow. When constructing a hydrograph--
- The base flow must be measured at a time when there have been no recent storms. A field reconnaissance must be made for this measurement.
- The peak flow can be estimated using the hasty runoff estimation presented in this chapter.
- The general shape of the curve of the hydrograph will be similar to that shown in Figure 6-5.
DRAINAGE-SYSTEM DESIGN
DESIGN DATA REQUIREMENTS
Before designing a drainage system, survey the various types and sources of drainage-related information. The survey should include, as a minimum, information concerning the area's topography, meteorological records, soil characteristics, and available construction resources.
TOPOGRAPHICAL INFORMATION
Give special attention to the vicinity of the proposed facility as well as the presence of any topographical features that may contribute runoff to the project area. The completed facility often will interfere with the site's natural drainage. Therefore, when analyzing the effects of the surrounding terrain--
- Identify all areas that contribute runoff to the site.
- Determine the general size and shape of these contributing areas.
- Determine the natural direction of surface-water flow, the slope of the land, and the type and extent of natural ground cover.
- Locate natural channels that can be used to move runoff within the project area or to divert it away from the work site.
METEOROLOGICAL DATA
Gather information on general climatic conditions, seasonal variations in rainstorms, and intensity and duration of representative storms. This data can then be applied to the location of the proposed facility.
SOIL CHARACTERISTICS
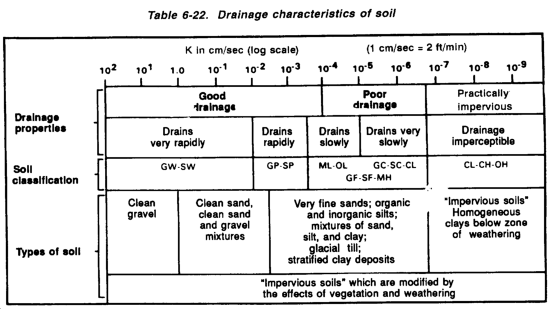
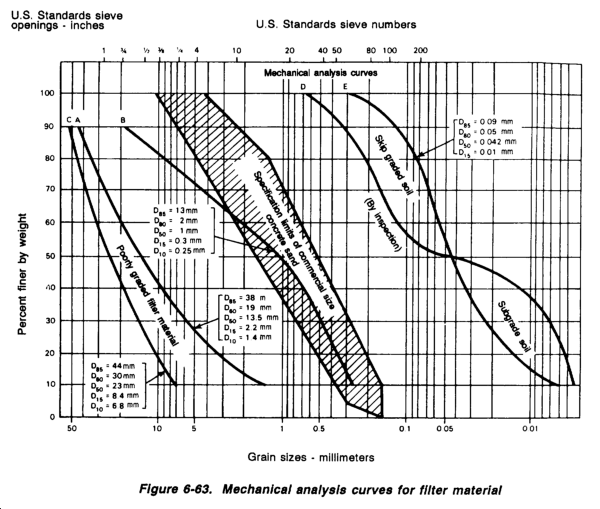
Obtain soil data from soil and geological maps, aerial photographs, or site tests performed by soil analysts. Soil data deals with the horizontal and vertical extent of soil types, the elevation of the groundwater table, and the drainage characteristics of the soil. The most important drainage characteristic of a soil is its permeability. Permeability limits the rate at which the rainfall infiltrates the ground, which greatly influences the presence and movement of subsurface water.
AVAILABLE RESOURCES
Make an initial investigation of the time, materials, equipment, and labor available to build a drainage system. Without a sufficient quantity of these essentials, the construction of an adequate system is impossible.
DESIGN PROCEDURES
Designing a drainage system involves numerous assumptions and estimates. The degree of protection to be provided is directly related to the importance of the established time-use period. The general location of the facility will be determined by its functional requirements.
The drainage system must be planned and designed for the predetermined location of the facility. There are three basic procedures in the design of any drainage structure:
- Determining the area (usually in acres) contributing runoff to the facility.
- Estimating the quantity of runoff.
- Designing the drainage structure to carry the maximum expected runoff.
DETERMINING THE AREA CONTRIBUTING RUNOFF
When developing a tentative layout for drainage system, identify all locations within the site requiring drainage structures because of topographical or manufactured features. This is best done from a topographic map of the area or a sketch of the project site.
Next, determine the acreage of the areas that contribute runoff to these required drainage structures. An analysis of existing channels is helpful in establishing locations for the required structures. Upon completion, this tentative plan should be field checked at the project site.
Establishing Drainage-Structure Locations
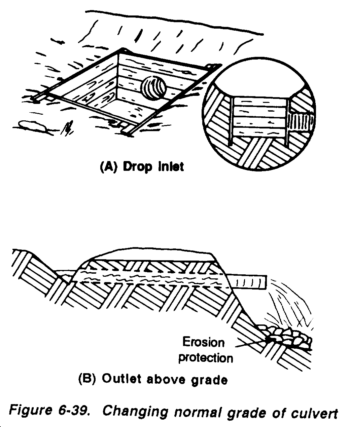
The initial step in developing a drainage-structure layout is to establish the location of the required drainage structures. Placement, in general. will be controlled by the topography. For example, a fill section which crosses a valley will require one or more culverts to permit the flow of storm runoff down the valley. A depression or enclosed area will require ditches or culverts at various points to remove accumulated rainfall.
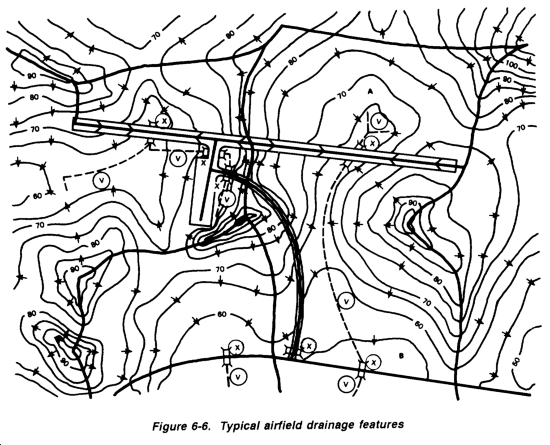
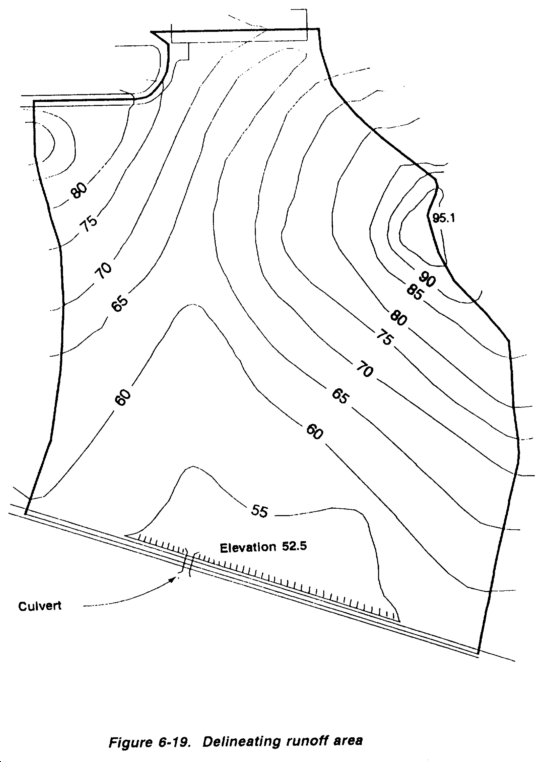
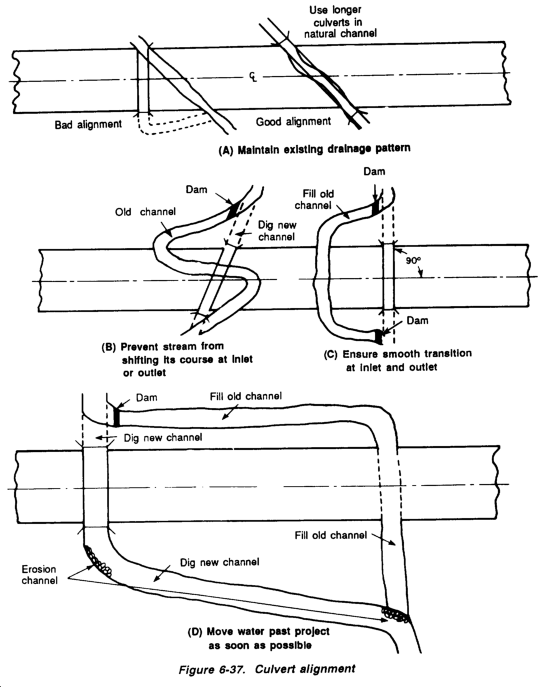
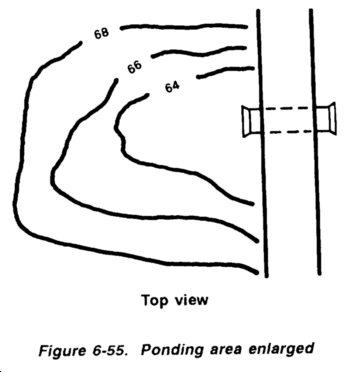
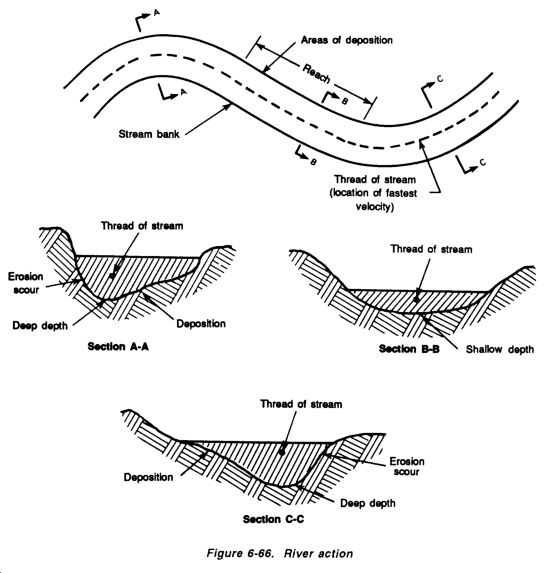
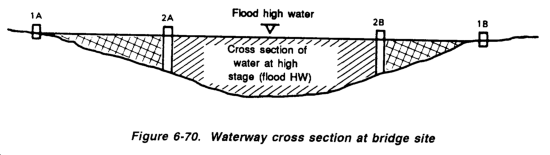
Figure 6-6 shows an airfield with required culverts (X) and open channels or ditches (V). Note that at Point A the elevation is 65 feet, while at Point B the elevation is 55 feet. Culverts and ditches must be laid to carry water from high to low elevations. The alignment of these culverts and ditches should be as straight and smooth as possible. Sharp bends in ditches or near culverts will cause erosion. Not shown on this sketch are the standard ditches constructed along the sides of all military roads and airfields.
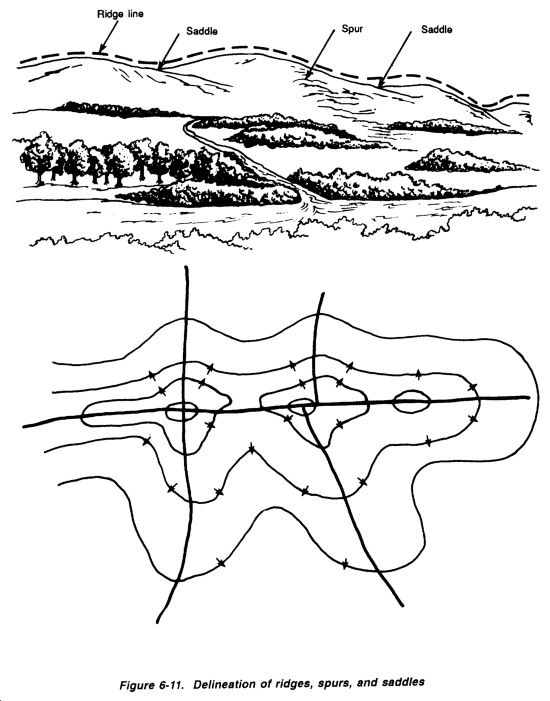
After initially locating drainage structures, define the boundaries of the areas (or watersheds) contributing runoff to each of them. This process is known as delineation. Delineation is performed in six simple steps (refer to Figure 6-6):
Step 1. Locate all existing or proposed drainage structures on the topographic map or sketch (X and V).
Step 2. Identify and mark all terrain high points.
Step 3. Draw arrows representing water flow away from these high points. (These arrows must always be perpendicular to the contour lines because water flows downhill.)
Step 4. Continue drawing the arrows until they converge upon the culvert or the end of the ditch. Remember that runoff will flow parallel to a road or airfield when it is intercepted by side (or interceptor) ditches.
Step 5. Draw delineation lines. (These lines will run from high point to high point, indicating where the flow of surface runoff separates.) Delineation lines are located so they cannot be crossed by any flow arrows. Flow arrows only cross delincation lines at culverts or ditches.
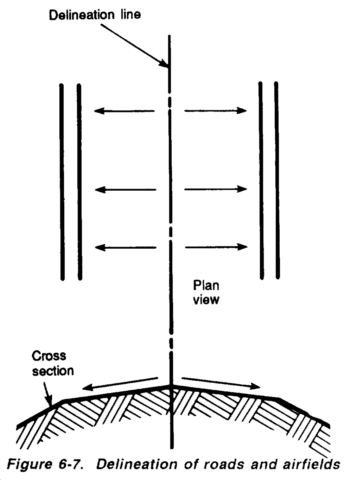
NOTE: Delineation lines are drawn between opposing arrows, (See Figure 6-7.)
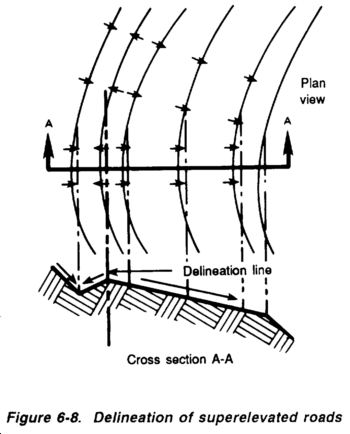
Figures 6-7 and 6-8 depict the use of flow arrows and delineation lines for special, manufactured structures such as roads, airfields, and superelevated roads. When airfields or straight roadways are properly constructed, they are shaped so that the highest portion of the cross section (the crown) is at the centerline, as illustrated in Figure 6-8. In the plan view, the delineation will be at the centerline precisely where the accumulated storm water would separate and flow in opposing directions. Figure 6-8, shows how superelevated roadways (roadways that are banked to ease the flow of traffic through a curve) are delineated. In a properly constructed, superelevated road, storm water will always separate at the outside edge of the curve.
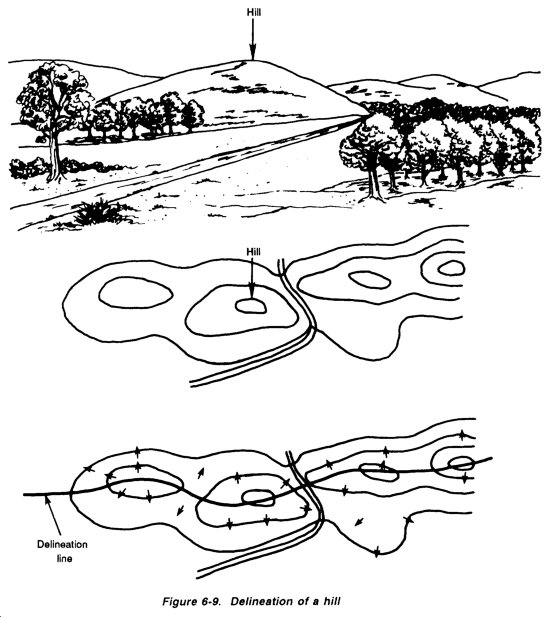
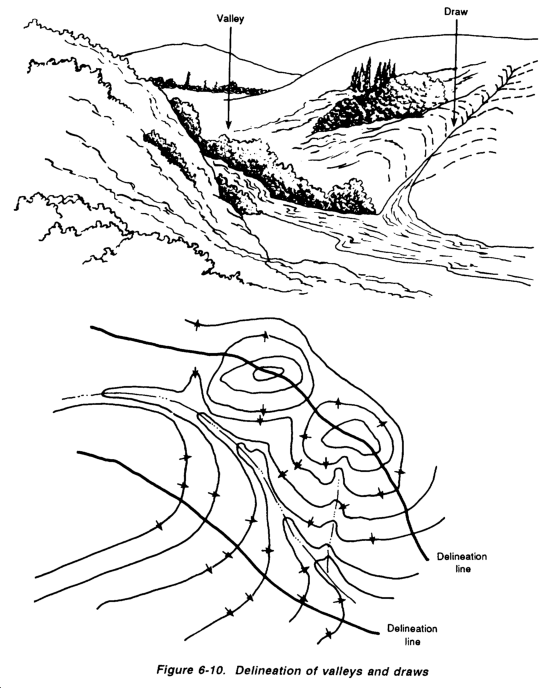
Several examples are provided to aid in visualizing special terrain features, including hills, ridges, valleys, and saddles, as shown in Figures 6-9 and 6-10 and Figure 6-11.
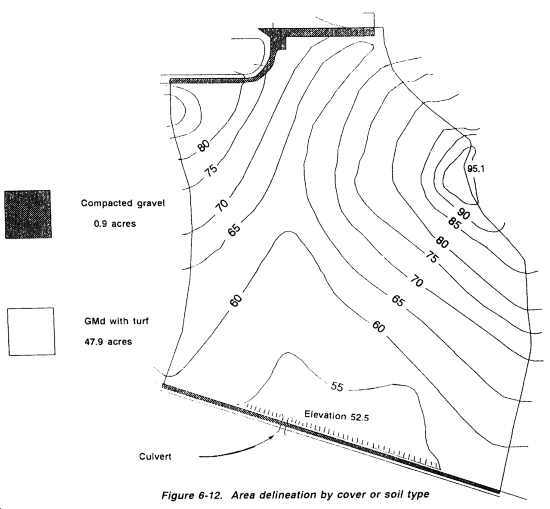
Step 6. Since each cover or soil type will have an effect on the basin, if there are multiple types of cover in the basin, each cover or soil type must be delineated and measured according to its respective cover type. (See Figure 6-12.)
Determining Drainage-System Size
After delineating the watershed determine its size in acres. Make this measurement carefully, since the size directly influences the calculation of runoff from the watershed at peak flow. Use any accurate method of measurement desired. A planimeter which measures the area of a plane figure as a mechanically coupled pointer traverses the figure's perimeter, is quite accurate and should be used, if available. However, several other methods are suitable for field estimation.
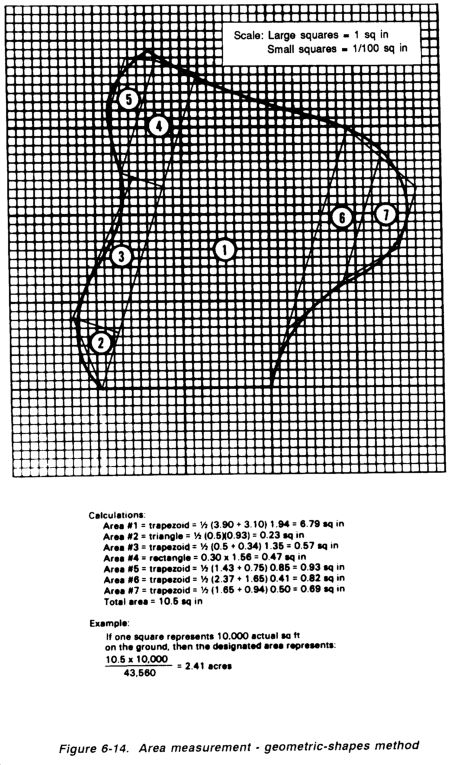
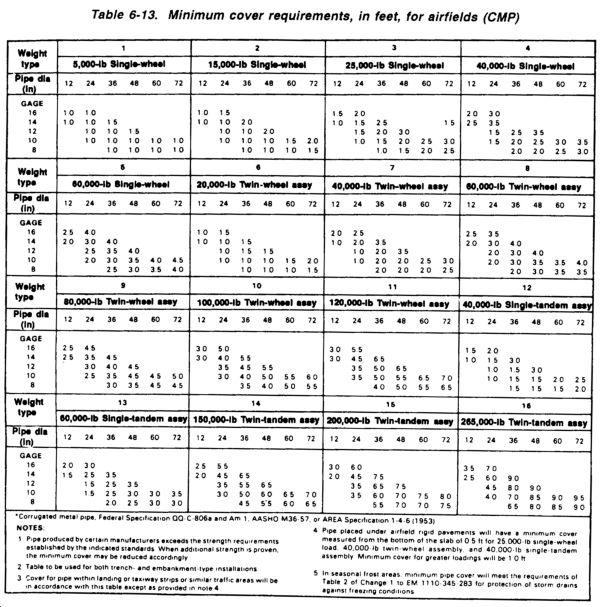
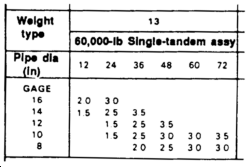
Counting-squares method. To make a hasty approximation of an area, transpose the outline of the watershed to graph paper (or other suitable grid). Count the number of whole squares and estimate the values of the partial squares Multiply the total number of counted squares by the number of counted square feet represented by a single square. Then convert the measurement in square feet to acres (1 acre = 43,560 square feet), Figure 6-13, shows this technique.
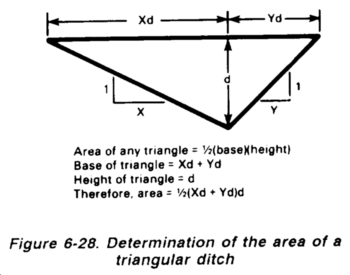
Geometric-shapes method. This method involves estimating the watershed shape in terms of rectangles, triangles, or trapezoids. Using the formulas below for determining the areas of these geometric shapes, determine the area of each shape and then total all areas to estimate the area of the watershed. This technique is shown in Figure 6-14.
Rectangle:
Triangle:
Trapezoid
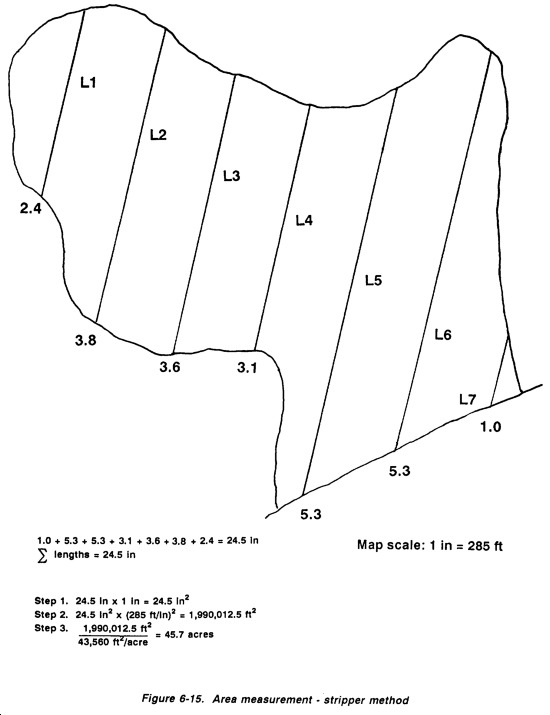
Stripper method. The stripper method is a variation of the geometric-shapes method. This method is shown in Figure 6-15. Approximate the area by drawing a series of lines that are equidistant (stripper width) across the delineated area. Then measure the lines and total all of them. L = total of the lengths. This method is more applicable for field estimations. Use a stripper width of 1 inch.
The total of the lengths (L) is then multiplied by the stripper width. This would represent the total area on the map in square inches. Since the value of 1 square inch on the map would represent the map scale squared on land, the acreage can be found by multiplying L (in inches) x stripper width (in inches) x (map scale in feel per inch (ft/in))2 and dividing the product by 43,560 ft2/acre.
Example:
L = 12.5, map scale = 175 ft/in, stripper width = 1 inch (in)
Solution:
Step 1. 12.5 x 1 in = 12.5 in2
Step 2. 12.5 in2 x (175 ft/in)2 = 382,812.5 feet (ft)2
ESTIMATING THE QUANTITY OF RUNOFF
Drainage systems must be designed to accommodate the peak flow generated by runoff from contributing watersheds during the design storm. Many techniques are available for determining the peak flow, but most are too complex for general field use.
This manual will demonstrate the most common method for estimating runoff--the rational method.
DESIGNING DRAINAGE STRUCTURES FOR MAXIMUM RUNOFF
To accommodate the peak flow of the design storm, design structures must provide a sufficient cross-sectional area and longitudinal slope for passing storm runoff. If pending or flooding of adjacent areas must be prevented, the design must be for peak flow. At the same time, water velocities generated at peak flow must not be so great as to cause damage to the drainage structure or excessive erosion and scouring 10 the protected facility.
Determine the capacity of drainage structures by calculating the runoff from all contributing drainage areas. Specific procedures for designing open channels and culverts are discussed later in the chapter.
ESTIMATING RUNOFF USING THE RATIONAL METHOD
ESTIMATING PRINCIPLES
The rational method is used to estimate the expected peak storm runoff at a given drainage basin outlet. Much of the input to the formula is based on judgment. Therefore, it is imperative that sound engineering judgment be used to determine the input data.
ASSUMPTIONS
The rational method is based on the following underlying assumptions and limitations:
- The area is not greater than 1,000 acres and is regular in shape, with a homogeneous cover and soil type.
- The entire drainage area is contributing runoff to the outlet point when peak runoff is obtained.
- The design rainfall intensity is uniform over the entire drainage area (that is, the rainfall is uniform over time and space).
- There are no active streams draining the area. (If an active stream drains the basin, use the hasty method found in FM 5-34.)
FORMULA
The rational method uses the following formula:
 = CIA
= CIA
where--
 = peak runoff in cfs
= peak runoff in cfs
C = runoff coefficient
I = intensity of rainfall in/hr
A = drainage area in acres
The following conversion factor is applied to this formula:
This is so close to unity that no correction factor is added; hence, the name rational (because a rational conversion of units) is used.
FORMULA VARIABLES
The rational formula has three variables. The C and I variables are explained here. The A variable is explained later in this chapter.
The C Variable
The runoff coefficient, or C variable, accounts for losses from precipitation. The C variable is the decimal fraction of the amount of water expected to run off relative to the amount of precipitation. It can be expressed as the ratio--
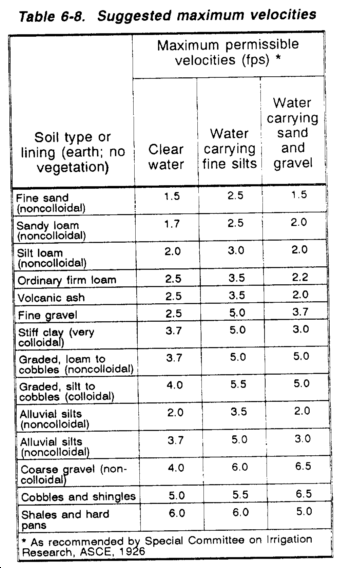
Table 6-1 gives conservative values of C. Knowledge of an area's USCS classification (for example, GMd) or an estimate of the soil's perviousness allows selection of a C value. C values appear in the table for manufactured surfaces and for wooded areas as well. An area of SP soil (a pervious, sandy soil with a slope less than or equal to 2 percent) with turf has a C factor of 0.10; that is, only 10 percent of the rain falling on this soil will actually run off.
The remaining 90 percent becomes lost to runoff through infiltration and other factors. At the other extreme, an asphalt pavement has a C value of 0.95. Only 5 percent of the rain falling on asphalt will be lost. The remaining 95 percent is expected to become runoff.
NOTE: C values given in Table 6-1 are actually maximums of ranges of allowable values for the cover or soil categories. Using the maximum value, a conservative "worst-case" design runoff is calculated. To use values less than the maximums given in the table, refer to a reliable civil engineering text dealing with hydrology. The table is arranged with three columns for varying slope conditions.
C Versus Slope
As terrain becomes steeper, water flows sooner and more rapidly. This allows less time for infiltration to occur and results in the C value becoming larger for the natural cover or soil categories. For this reason, whenever the average slope of an area exceeds 2 percent, an adjustment must be made.
Table 6-1 is arranged with three columns for different slope conditions and their corresponding runoff coefficients. Use the column that corresponds with the average percentage of slope.
The C for a turfed soil is different from the C for bare soil. The turf (grass or other ground cover) exerts a drag on water, causing slower flow and providing more time for infiltration to occur; hence, a lower C results. Denuded soil (soil from which the turf or cover has been removed) requires an increased C because a swifter flow will result and less time will be available for losses to occur. If one cover type has more than one flow path, average the slopes and use the appropriate column in Table 6-1.
Example:
Flow path 1A = 2.3 percent and flow path 1B = 1.9 percent.
Solution:
C for Nonhomogeneous Areas
One of the assumptions made by the rational method is that there is a homogeneous cover and soil type throughout the area. Quite often this is not the case, especially in areas where humans have exerted their influence on the topography.
If one type of cover and soil predominates in 80 percent or more of the area, the area is called simple and the C value for that predominant soil and cover type controls. If no one type of cover and soil type predominates in 80 percent or more of the total area, the area is complex and the C value must be weighted; that is, the C value has to be adjusted to account for the proportion of C contributed by each subarea.
To help understand this, imagine a complex area with one subarea of average turf and the other of bare soil. The slope of the bare soil does not affect how fast (or slow) the water runs off the turfed area and, as a result, how much of the water soaks into the turfed area. The converse is also true. The slope of the turfed area does not affect the speed or amount of water that runs off the bare soil area. Table 6-1 shows C values with and without turf.
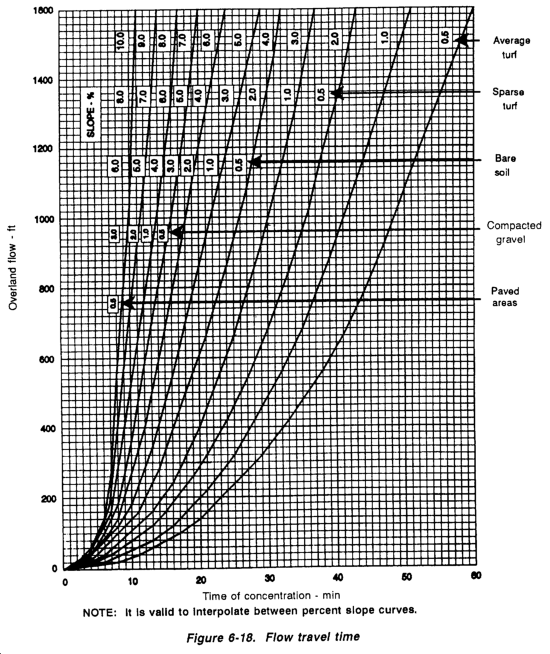
Weight the C value by multiplying the corrected C values by the area (in acres) that the C values affect. Then total the products and divide by the total acreage. Expressed mathematically, the formula is--
where--
C1A1 = C value and area for first subarea
C2A2 = value and area for second subarea
The I Variable
As explained previously in this chapter, rain-fall intensities can be determined from pinpoint source data or isohyetal maps. The former method provides more accurate results if reliable data is available. The task of calculating the critical duration for any given drainage area is detailed here.
Under the assumptions listed at the beginning of this section and with the intensity-duration relationships presented earlier, only one particular storm will give a maximum discharge ( ) for a given area. This particular storm is the one that rains over the entire area being drained for a period of time just long enough to fill the outlet with runoff from all segments of the area at the same time. This time is called the area TOC. A storm of shorter duration than this TOC would not last long enough for the runoff from the more distant segments of the area to reach the outlet. The outlet would be filled only with the runoff from nearby segments. Therefore, runoff would not be maximum.
) for a given area. This particular storm is the one that rains over the entire area being drained for a period of time just long enough to fill the outlet with runoff from all segments of the area at the same time. This time is called the area TOC. A storm of shorter duration than this TOC would not last long enough for the runoff from the more distant segments of the area to reach the outlet. The outlet would be filled only with the runoff from nearby segments. Therefore, runoff would not be maximum.
In Figure 6-16, all of the area below the 10-minute line will drain in 10 minutes or less. Runoff from the area between the 10- and 20-minute lines will reach the outlet in not less than 10 minutes but will have drained in not more than 20 minutes. Similarly, the runoff from the area between the 20- and 30-minute lines will reach the outlet in not less than 20 minutes nor more ban 30 minutes. At the end of 30 minutes the entire area is draining. Therefore, the TOC at the outlet for this area is 30 minutes.
If a storm of 20-minute duration sweeps over the area in a uniform fashion, only a fraction of the total area inside the 20-minute boundary simultaneously contributes runoff to the outlet at the end of the storm. All runoff from the upper third of the area reaches the outlet after the rainfall has ceased and after much of the lower acreage has finished contributing runoff.
If a 30-minute-duration storm sweeps over the same area in a uniform fashion, the entire area contributes runoff to the outlet in the 30-minute time frame (the TOC mentioned above).
If a storm with a duration longer than the TOC occurs, the drainage designer can easily picture (using the standard intensity-duration curve) that the intensity, I, will be less than the I of the 30-minute storm. Examination of the rational-method equation,  = CIA, reveals that since C and A would not change as I decreases,
= CIA, reveals that since C and A would not change as I decreases,  must decrease as well. The critical-storm duration which yields the design
must decrease as well. The critical-storm duration which yields the design  must then be equal to the contributing area's TOC.
must then be equal to the contributing area's TOC.
Determine the area TOC by determining representative flow paths. A flow path is the path that a typical drop of water will follow from the time it hits the ground until it reaches the area outlet. The flow path is called representative, because not all drainage areas are as regular in shape as the area in Figure 6-16. The path selected must be representative of the time at which most of the area will be contributing water to the outlet point. Establishing representative flow paths is based largely on experience and judgment (trial and error).
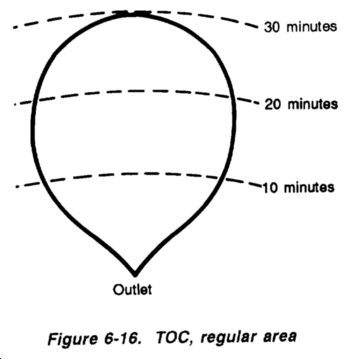
Unlike the area depicted in Figure 6-16, the area in Figure 6-17 is irregular as most natural areas will be. In irregular areas, it is especially critical that the flow paths chosen truly represent the time required for most of the area to drain. All the area below the 10-minute line will drain in 10 minutes or less. The area between the 10- and 20-minute lines will drain in not less than 10 minutes nor more than 20 minutes and so forth up to the 40-minute line. Flow lines a, b, and c have been determined; 90 percent of the total area (90 acres) lies below the 30-minute line and will drain in 30 minutes or less. Water from the remaining 10 acres will reach the outlet in not less than 30 minutes nor more than 40 minutes. Flow lines a and c should be chosen as the representative flow paths and used to determine the TOC because they are indicative of the time it will take for most of the water from the area to reach the outlet. Line b is not representative.
For simplicity, in this example let C arbitrarily equal 1.0 and assume that the 1-hour, 2-year intensity is 2,0 inches per hour. If a 40-minute-duration storm occurs, in 40 minutes the entire area will be wet and contributing water to the outlet point. The standard intensity-duration curve in Figure 6-4, shows that the I for a 40-minute storm is 2.7 inches per hour; therefore, the estimated runoff is--
 = CIA
= CIA
 = (1.0)(2.7 in/hr)(100 acres) = 270 cfs
= (1.0)(2.7 in/hr)(100 acres) = 270 cfs
A storm of 30-minute duration will have an intensity of 3.2 inches per hour. At the end of 30 minutes, 90 percent of the area (90 acres) will be contributing water to the outlet and the volume will be--
 = CIA
= CIA
 = (1.0)(3.2 in/hr)(90 acres) = 288 cfs
= (1.0)(3.2 in/hr)(90 acres) = 288 cfs
which is larger than the 270 cfs estimated for the entire area.
Flow paths must be chosen that represent the time required for most of the area to drain. As shown above, a shorter storm of higher intensity may cause a larger flow. After all the chosen paths have been timed, the times should correspond to each other within a few minutes. If times are not relatively close, make a careful check to determine why, and assess the area to determine which of the times will produce the critical flow. Apply rainfall adjusted to this critical duration over the entire watershed. The design runoff from the watershed in Figure 6-17 would be--
 = CIA
= CIA
 = (1.0)(3.2 in/hr)(100 acres) = 320 cfs
= (1.0)(3.2 in/hr)(100 acres) = 320 cfs
After representative flow paths have been established, estimate the time it will take for water to reach the outlet if it travels along the established path. To do this, determine (through observation) the nature of the surface cover and the slope of the flow path. Slope affects the velocity of the water in that the steeper the slope, the faster the water runs. Water will also travel faster across a paved area than across a grassy area of the same slope because grass slows the flow. Flow is slower over bare soil than over pavement but faster than grass. Flow in a ditch is more rapid than overland flow over turfed, bare, or compacted gravel surfaces.
Estimating Flow Time for Single Covers
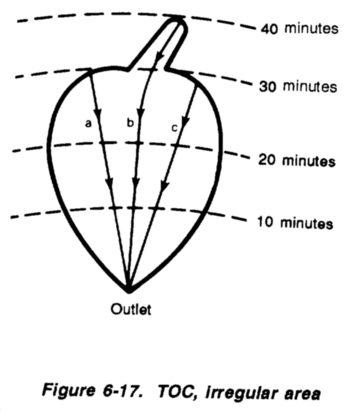
After establishing the location, the cover, and the slope of a flow path, Figure 6-18 can be used to estimate the travel time along the flow path. It is important to understand what the illustration is depicting as well as how to use it properly.
Notice that there is a series of curves, each with linear and curvilinear portions. The slope of the curve indicates the velocity at a given point along the flow path. In the curvilinear portion, the slope is initially zero and gradually steepens until it becomes linear. This represents the fact that water initially moves very slowly and begins to pick up speed only as its accumulated depth increases. It is initially slow flowing in a laminar or sheet-flow manner and gradually becomes turbulent (and faster) as it progresses downhill. At some point, the turbulent-flowing water reaches some steady-state velocity. It is apparent from Figure 6-18 that the slope and "slickness" of the flow path dictate how quickly the transition occurs from slow-moving laminar flow to rapid, fully developed turbulent flow
To estimate the travel time in sheet-flow conditions, use Figure 6-18. Enter the right-hand vertical edge at the appropriate cover type of the flow path. Proceed horizontally to the left until reaching the curve labeled with the slope of the path. Follow the curve up or down until you reach the intersection of the horizontal line equaling the flow-path length, which is determined on the left-hand vertical edge. Read the travel time, which is found by drawing a line vertically from the intersection to the lowermost axis. Some examples of the use of this graph are as follows:
|
|
|
|
|
Travel |
|
|
||||
|
1 |
Sparse |
800 |
3.0 |
19 |
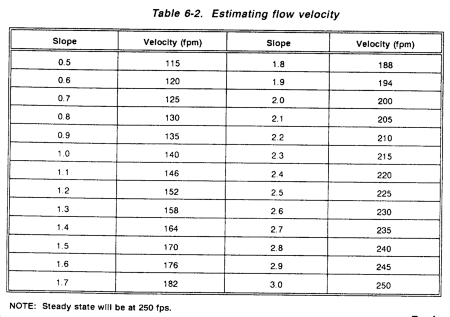
Note that it was necessary to interpolate to find the travel time for path 3. It is valid to interpolate between labeled lines, but never extrapolate above or below the limiting-curve values. Use the limiting curve in that situation. To estimate the travel time in ditch-flow conditions, use Table 6-2. Using the slope of the flow path, enter the chart, then read the right-hand column under velocity. To calculate the velocity, divide the length of the path by the velocity obtained from the chart.
Example:
Path 1B
Cover - Ditch
Length - 1,015 ft
Slope - 0.9%
Chart velocity - 135 feet per minute (fpm)
Solution:
Estimating Flow Time for Multiple Covers
In many cases, a flow path traverses more than one cover type. Estimating travel time accurately then becomes more complicated because it is not appropriate simply to add times obtained from Figure 6-18. Laminar flow occurs only once along a flow path, no matter how many cover types are traversed. For subsequent covers, it becomes necessary to estimate flow velocity using Table 6-2.
To estimate travel time in a ditch, use Table 6-2. Enter the table using the slope of the flow path. Then read right to the velocity column and find the velocity in feet per minute. By knowing the flow-path length and the table velocity, the travel can be calculated.
Example:
Assume that paths 1 and 2 from the preceding example were actually the upper and lower lengths of one combined flow path. To estimate their combined travel time, first estimate each separately in the order the water would flow through them.
Solution:
Estimate the travel time of path 1. Since path 1 is uphill from path 2, nothing has changed from before. The travel time remains 19 minutes. Estimate the travel time of path 2. Remember that the flow entering at the upstream end of path 2 is al ready moving. To estimate travel time, divide the length of the path by the estimated velocity listed in Table 6-2. In this case, for a 500-foot, paved path at 1.5 percent--
(Note that path 2 had an 8-minute travel time when considered alone.)
Arid partial travel times to get the total travel time:
Travel time = 19 min + 3.0 min = 22 min
It may be helpful, at times, to estimate the travel time through a culvert. A reasonable assumption of culvert velocity is 5 feet per second (fps) (300 fpm), although more precise determinations can be made with information presented later in this chapter.
Selecting Design TOC
The usual procedure is to establish several trial flow paths that are thought to be representative of the area and determine a travel time for each path. Compare the time for water to travel along each of the flow paths chosen. If the times are within a few minutes of each other, select the longest time as the area TOC. If the times are not within a few minutes of each other, make a complete analysis of the area. New flow paths may be needed to determine which of the times is representative of the bulk of the area draining. The largest representative time is chosen as the design TOC.
The A Variable
The drainage area, A, (the area contributing storm-water runoff to the culvert or ditch being designed) must be calculated in acres. This procedure was presented earlier in this chapter.
APPLYING THE RATIONAL METHOD
Application of the rational method of estimating drainage varies according to the type of drainage area. One type is a single, independent area which does not receive any drainage from an upstream area. Another type is a dependent or successive area that receives runoff from another area.
Single Areas
The rational method of estimating single areas is reasonably simple and straightforward, if it is done methodically. The steps are summarized in the proper order. If this summary is followed step-by-step, the procedure will be correct and the estimate obtained will be as valid as the judgments that are made.
Step 1. Delineate the area to determine the area contributing runoff to your project location. Refer to Delineating Watersheds.
Step 2. Delineate subareas by soil or cover type. Refer to Delineating Watersheds Step 6.
Step 3. Determine acreage for each basin and subarea. Refer to Determining Drainage-System Size.
Step 4. Classify the drainage basin as simple or complex. A simple watershed has one cover or soil type over 80 percent of its total area. A complex watershed has no single cover or soil type covering at least 80 percent of its total area.
Step 5. Determine representative flow paths. Refer to Determining TOC.
Step 6. Divide flow paths into two sections: laminar and ditch flow. As a rule of thumb, use 500 feet plus or minus 200 feet as a point where laminar flow will change to ditch or steady-state flow. Generally, overland flow concentrates into natural rivulets or channels after roughly 500 feet of travel. This distance may vary up to several hundred feet either way, depending upon such factors as soil type, vegetation, and slope. It is always best to visually investigate on-site to look for evidence of channeling, and take measurements accordingly. However, since in this problem it is not possible to visually investigate the drainage area, clues to determine when overland flow (sheet flow) ends and ditch flow begins must come from topographic information alone. Some of these clues may be the beginning of uphill swales or flow paths that converge in a swale. This convergence may take place in a valley where multiple paths meet.
Step 7. Determine the slope of each section of flow path. See Determining TOC.
Step 8. Determine the average slope of the basin or each subarea based on flow paths. Define the slope as being either <2%, > 2% and < 7%, or > 7%.
Step 9. Find the C value of the basin or each subarea based on soil or cover type and slope from Table 6-1. Select C from the appropriate column in Table 6-2, making sure that you pick the right C-value column. Notice that the columns are arranged with respect to slope and cover type.
Calculate Cwtd, if the area is complex.
Step 10. Determine the travel time for each flow path and select the longest flow path as the basin TOC. Refer to sheet flow and ditch flow in Table 6-2.
Step 11. Find I for a 2-year, 60-minute storm on the world isohyetal map (Figure 6-3)
Step 12. Adjust I based on the TOC (step 10), using Figure 6-4.
Step 13. Calculate  using C from step 12, and A from step 3 as follows:
using C from step 12, and A from step 3 as follows:  =CIA.
=CIA.
Estimate the amount of runoff expected to arrive at the culvert in Figure 6-19.
The location is Giessen, Germany, and the design life is two years.
NOTE: A number of steps, quantities, and calculations will be "given" to illustrate the process.
Solution:
Step 1. Delineate the area. (Given for this example.)
Step 2. Delineate the subareas by soil or cover type. (Given for this example.)
Step 3. Determine the acreage for each basin or subarea. The following acreage is given for this example:
|
Average turf GMd |
47.9 acres |
|
Compacted gravel |
0.9 acre |
|
Total acreage (A) |
48.8 acres |
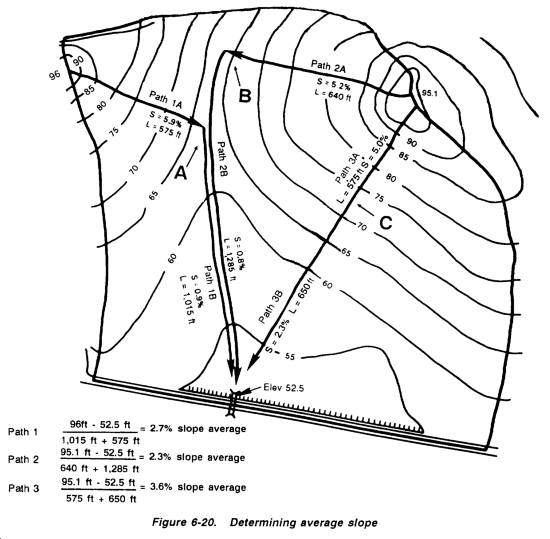
Step 4. Classify the drainage basin as simple or complex. Divide the largest soil or cover group (the GMd soil) with turf subarea equaling 47.9 acres by the total area, 48.8 acres.
Since the percentage is greater than 80, this area will be treated as a simple area consisting of 48.8 acres of turfed GMd soil.
Step 5. Determine the representative flow paths. It is necessary to determine the average slope of the entire simple area shown in Figure 6-19. In order to do this, use representative flow paths. If the north south running swale is imagined as the dividing line, approximately one-third of the watershed area lies to the west (left) and two-thirds to the east (right). To determine an average slope, the number of slope measurements taken on the western slope should be balanced by twice that number taken from the east. Figure 6-20 reflects this guideline, showing three slope measurements, two on the east and one on the west.
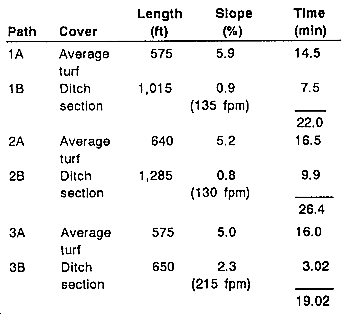
NOTE: The selection of representative flow paths is a judgment call based on the best evaluation of the topographic features.
Step 6. Divide flow paths into two sections: sheet and ditch flow. Generally, overland flow concentrates into natural ditches after 500 feet. Path 1 changes to ditch flow in the valley where it slopes down. See section A of Figure 6-20. The same is true for path 2. By looking at the contour lines near path 3, we can see they are relatively flat. Flow occurs across a wide area, and no clear point can be seen where the flow changes. A good estimate would be at 575 feet.
Step 7. Determine the slope of each flow path. The representative flow paths selected in an earlier step, if properly selected, can provide very good slope information with a minimum of effort. Other slope lines may be selected for practice and to gain confidence in using this procedure. Remember to maintain the 2-to-1 balance in finding slopes in this basin and to delete redundant information. The slope must be measured over a path that water would actually follow as it flows downhill. Normally, all work would be performed on one consolidated map. For instance, to determine the slope for path 1A--
This procedure is repeated for every flow path illustrated in Figure 6-20.
A tabular solution is recommended to determine TOC.
The slope of the original path 3 is unchanged, remaining at 3.6 percent. Paths 2A and 2B are now one single path, 2, with an average slope of 2.3 percent. (The average of 5.2 percent and 0.8 percent is not 2.3 percent.) Redetermine the overall slope (as done earlier). The earlier path 1B has been deleted, leaving only the original path 1A (with S = 5.9 percent) as the new path 1. The reason for deleting 1B is that it provides the same information already provided by the new path 2. Path 2B could have been deleted instead of path 1B with no change to the final result.
Step 8. Determine the average slope of the basin or subarea based on flow paths. With the three flow paths now determined, the average slope of the simple area is--
Step 9. Find the C value of the basin or subarea based on soil or cover type and slope from Table 6-1. Since we know that the average slope is 3.93 percent, we can use Table 6-1. Using the column marked slope 2% and <7% with turf, we have a C value of 0.35.
Step 10. Determine the travel time of each flow path and select the longest flow-path travel time as the basin TOC. Times for paths 1B and 2B were obtained by dividing their flow lengths by approximate velocities obtained from Table 6-2. The travel times for each of the complete flow paths (22.0, 26.4, and 19,02 minutes, respectively) are obtained from Figure 6-18. The variation between the smallest and largest time, although not small, is not excessively large, either. Perhaps path 1 is not representative and some ditch flow occurs along path 3 that could not be determined from the topographic information available. Both of these possibilities are likely to be true. However, without an actual field investigation to justify revising either path 1 or 3, accept the travel times already determined and select the largest as the basin TOC. Thus, TOC = 26.4 minutes.
Step 11. Determine the I value for a 2-year, 60-minute storm. To determine factor I, a source of rainfall data is necessary. The choice is between using pinpoint data (the most accurate means of determining 1) or referring to an isohyetal map. Since pinpoint data is not available, use an isohyetal map. Refer to the isohyetal map in Figure 6-3. Knowing that the airfield is located near the demilitarized zone (DMZ) in Korea, as shown in Figure 6-3, rainfall intensity of the 1-hour, 2-year storm is determined to be 2.5 inch per hour or--
I60, 2 yr = 2.5 in/hr
Step 12. Adjust the I value. To determine I, I60, 2 yr must be adjusted so that its duration is equal to the basin TOC, 26.4 minutes. Use the set of standard intensity-duration curves in Figure 6-4, to make the adjustment. Using curve 5 (for 2.5 inches per hour) and sliding along until the 26.4-minute imaginary vertical line is intersected, the intensity (adjusted to 26.4 minutes) is found to be 4.2 inches per hour; thus--
Iadj = I26.4 min, 2 yr = 4.2 in/hr
Step 13. Calculate  using C from step 9, Iadj from step 12, and A from step 3.
using C from step 9, Iadj from step 12, and A from step 3.
All the variables have been determined to solve the equation  = CIA, as follows:
= CIA, as follows:
C = 0.35
I = 4.2 in/hr
A = 48.8 acres
 = 0.35 x 4.2 in/hr x 48.8 acres
= 0.35 x 4.2 in/hr x 48.8 acres
 = 71.74 cfs or 71.7 cfs
= 71.74 cfs or 71.7 cfs
The determination of  is the final solution to the example.
is the final solution to the example.
If area 5 had been a complex area, steps 1, 2, 3, and 5 would be unchanged. The only difference would occur in step 4, which would be changed as follows:
Step 4 (for a complex area). An Savg for each soil or cover area must be determined (except for manufactured covers). A C value for each soil or cover must be determined based on the average slope for each cover area. Once all C or Cwtd corrections are made, then an area-weighted C or Cwtd can be determined. Cwtd would be used in solving  = CIA.
= CIA.
Successive Areas
Up to this point, the drainage areas discussed have been single, independent areas, whether simple or complex. These independent areas do not receive runoff from an upstream area. Some drainage systems, however, consist of a series of drainage areas with upstream areas discharging runoff into lower areas. The areas receiving this runoff are called dependent areas. The runoff accumulates and increases in its passage through the system.
Sometimes, two or more areas discharge runoff into the same dependent downstream area. Such contributing areas are called parallel areas.
Unfortunately, the increase in runoff is not the simple summation of the peak runoff of each individual area. The individual peak flows are acted upon by various factors, including storage and peak-flow reduction while in the drainage network. Also, the peak flow from upstream areas and the peak flow from downstream, dependent areas will probably not arrive at the lower outlet simultaneously. Hence, the total peak flow must be less than the total of the individual peak flows.
Calculating TOC
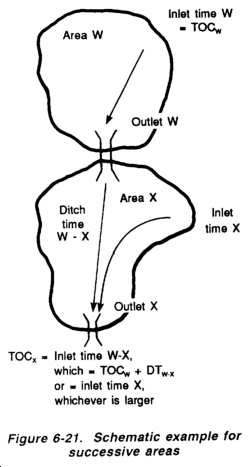
Because of the accumulation of peak flow in successive areas, calculation of TOC for those areas must be different from the method used for single, independent areas. To estimate the amount of the accumulated runoff with some precision, a procedure has been developed to recalculate TOC for each of the successive drainage areas as water travels downstream. Naturally, as TOC increases, rainfall intensity, I, decreases.
The term TOC must be modified to reflect calculation differences. Consider two areas, an upstream area W and a downstream area X, as shown in Figure 6-21. The maximum travel time from the most hydraulically remote representative points in this series of two areas to the outlet of area X is defined as TOC. The maximum representative flow times for runoff originating in both areas (X and W) to arrive at their respective outlets (X and W) are defined as inlet time X and inlet time W, respectively.
The TOC at the outlet upstream in area W is given as TOCw which equals inlet time W for this independent area. The ditch time (DT) or transit time through area X, from outlet W to outlet X, is DTW-X. The total of these two elements (TOCW and DTW-X) is inlet timeW-X.
To a designer engaged in sizing the culvert which serves as outlet W, the TOC would simply be TOCW = Inlet TimeW. However, when sizing culverts that occur further down in successive areas (for instance, the culvert at outlet X), the designer requires the time it takes water to arrive from the most hydraulically remote location, which might be in either area X or area W. To determine this maximum representative time (TOCX), the designer must compare the travel times for runoff origination in both areas.
The travel time for water originating in area W and arriving at outlet X is equal 10 the inlet lime at area W (which is the same as TOCX, since area W is dependent) plus the transit time as the water flows in a ditch through area X. This composite time, called timeW-X, inlet must be compared to the time for water that originates in area X, or inlet timeX. TOCX, the maximum representative time for water to arrive at outlet X, is the larger time value identified in the comparison.
Estimating Successive Area Runoff
The modified definition of TOC is applied in estimating runoff for successive areas. This calculation requires collection of certain essential data and application of the principles used for single areas, appropriately modified, to determine the desired Q.
Preparatory Work.
Step 1. Delineate every subarea in the series of areas.
Step 2. Determine the intensity of the 2-year, 60-minute rainfall.
Step 3. Determine A, C, and inlet time. For each subarea, determine the acreage (A); variable C, corrected for slope and weighted (as necessary); and the inlet time.
Step 4. Determine the DT (or transit time).
For each dependent subarea, the DT is determined from the upper outlet 10 the lower outlet using culvert flow (assume 300 fpm, you unless have more precise data).
Determining Specific  . Working systematically, start at the uppermost subarea and proceed downstream. Refer to Figure 6-21 and note that subarea W is upstream from subarea X.
. Working systematically, start at the uppermost subarea and proceed downstream. Refer to Figure 6-21 and note that subarea W is upstream from subarea X.
Step 1. Determine the subarea TOC using these simple rules:
The rule for an independent subarea is--
TOCW = Inlet timeW
The rule for a dependent area is--
TOCW + DTW-X
Compare inlet timeX with inlet timeW-X. Select the larger value of TOCX based on the comparison.
Step 2. Adjust I60min, 2yr to ITOC, 2yr.
Step 3. Calculate  for subarea W.
for subarea W.
 W = CWITOCxAw
W = CWITOCxAw
Step 4. Proceed downstream to subarea X and repeat steps 1, 2, and 3.
 X = CxITOCxAw
X = CxITOCxAw
Step 5. Total the accumulated runoff. To get the total runoff at the Outlet of subarea X, use the following equation:
 outlet x =
outlet x =  x +
x +  w
w
Step 6. Continue working downstream. Proceed until the runoff at the lowest outlet in the series is calculated. Use the drainage basin's corresponding rainfall intensity for the I value; use the total area for all basins and the subareas for the area. A value, in the rational-method formula.
 = CIA
= CIA
NOTE: Remember that when using the rational method, the area limit is 1,000 acres. Always check the accumulated acreage to ensure that it does not exceed 1,000 acres.
Example:
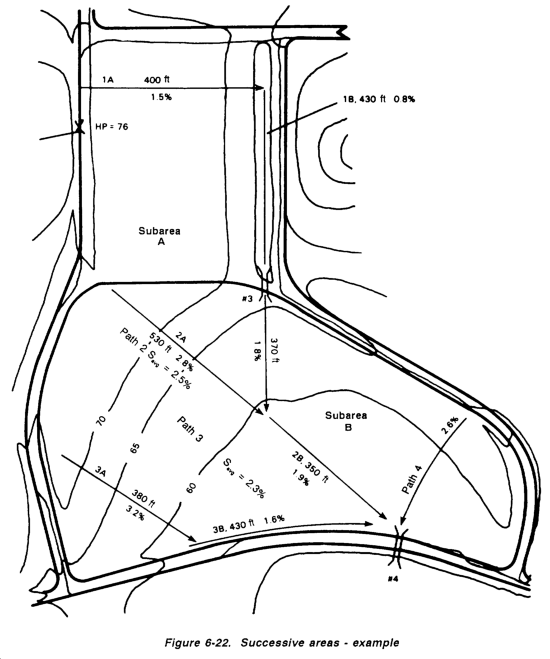
Using the rational method and Figure 6-22, determine the runoff, in cfs, expected at culverts 3 and 4 at the Span II Army Airfield at Giessen, Germany. The soil type is GMd.
Solution:
Step 1. Delineate the area; it is found to have the following:
Subarea A.
| Compacted gravel | 6.2 acres | Simple | ||
| Average turf | 0.2 acre |
Area | ||
| 6.4 acres |
Subarea B.
| Compacted gravel | 0.9 acres | Simple | ||
| Average turf | 12.5 acres |
Area | ||
| 13.4 acres |
Step 2. Delineate subareas by soil or cover type. (See step l.)
Step 3. Determine acreage for each basin or subarea. (This information is given in step 1.)
Step 4. Classify the basin as simple or complex.
Subarea A.
| Compacted gravel | 6.2 acres | |||
| Average turf | 0.2 acre |
Simple | ||
Total |
6.4 acres |
6.2 acres/6.4 acres = 0.97 or 97%
Subarea B.
| Compacted gravel | 0.9 acres | |||
| Average turf | 12.5 acres |
Simple | ||
Total |
13.4 acres |
12.5 acres/13.4 acres = 0.93 or 93%
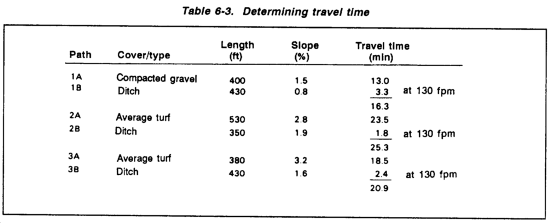
Step 5. Determine representative flow paths. See Table 6-3 (given information).
Step 6. Divide flow paths into two sections: sheet flow and channel flow. See Table 6-3 (given information).
Step 7. Determine the slope of each section of the flow path.
Step 8. Determine the average slope of the basin or each subarea. There are two paths in subarea 1, paths 1A and 1B. Both of these paths will have an average slope of less than 2 percent. Subarea 2 has three major paths. Path 2 has an average slope of 2.3 percent, path 3 has an average slope of 2.4 percent, and path 4 has an average slope of 2.6 percent. (See Figure 6-22.) Using this information, we can now get an average slope for paths 2, 3, and 4.
Average Slope = Average slope for subarea 1 = <2%
Average slope for subarea 2 = 2.4%
Step 9. Find the C value for each subarea., Subarea A has compacted gravel with an average slope less than 2 percent. Using Table 6-1, we find that the C value is 0.70. Likewise, the C value for subarea B, GMd with average turf with a slope of 2.4 percent, is 0.35.
Step 10. Deter mine the travel time of each flow path and select the longest flow-path travel time as the TOC. Obtain sheet-flow times from Figure 6-18, and ditch-flow travel time from Table 6-2. Determine the travel times and ditch time from Table 6-3.
Step 11. Determine I and Iahj (I value for Giessen, Germany is 1.7 in/hr from local rainfall records.)
Subarea A.
TOCA = 16.3 min
I16.3 = 2.6 in/hr
Subarea B.
Compare inlet timeB = 25.3 min with TOCA + DT = 16.3 + 3.8 = 20.1 min
Select the larger value of TOCB = 25.3 min and I25.3 = 1.8 in/hr
Step 12. Adjust I based on TOC using Figure 6-4. (This step was included in step 11.)
Step 13. Determine runoff.
To calculate runoff in subarea A, use--
 A A |
= CAIAAA |
| = 0.70(2.6 in/hr)(6.4 acres) | |
| = 11.6 cfs |
To calculate runoff in subarea B, use--
 B B |
= CBIBAA |
| = 0.35(1.8 in/hr)(13.4 acres) | |
| = 8.4 cfs | |
 inlet 3 inlet 3 |
= 11.6 cfs |
 inlet 4 inlet 4 |
= 11.6 + 8.4 = 20 cfs |
NOTE: Although path 4 was used to obtain an accurate slope average, it is not used for travel time. The situation, as drawn on the map, clearly shows that path 4 could not be chosen for the TOC.
SECTION II. OPEN-CHANNEL DESIGN
An open channel is a conduit with a free-water surface used to convey water. The most common is a ditch, which is an open channel cut into the soil. If so desired, the ditch can be lined along the bottom from bank to bank.
The size, the shape, the method of construction, and the location of a ditch are deter mined largely by its purpose. These factors, once determined, will influence the design capacity and maintenance requirements.
DESIGN FACTORS
LOCATION
There are three main types of ditches used in road and airfield construction.
An interceptor ditch is generally located on a hillside above a roadway or other feature requiring protection. Its function is to intercept runoff and direct the flow to a more desirable location. It is usually located above sidehill cuts to prevent erosion of the cut.
A side ditch is located along the side of a road. It collects runoff from the road and adjacent areas and transports it to a culvert or diversion ditch.
When the topography allows, a diversion ditch is built to transport water away from roadways or airfields. It can be used in conjunction with interceptor and side ditches to transport water between culverts or to divert an existing stream channel around a project.
CROSS SECTION
The location and peak quantity of runoff expected will determine the ditch cross-sectional area required. The most common shapes of cross sections--triangular (symmetrical and nonsymmetrical), trapezoidal, and segmental--are shown in Figure 6-23.
In the TO, the shape of a ditch is also dictated, to a great extent, by the choice of engineer equipment available for its construction. Two items of equipment are uniquely suited for speedy ditch excavation: the motor grader and the wheeled tractor-scraper. Other items of equipment that can be used to excavate a ditch section include the backhoe; bulldozer; front-end loader; trenching machine; and crane equipped with a dragline, clamshell, or shovel front.
However, production rates for these items are relatively low compared to the grader or scraper; hence, the grader or scraper is more likely to be used.
Triangular or V ditches are commonly installed to handle flows up to 60 cubic feet per second. The road grader is well designed to quickly excavate the necessary cross section to handle this flow, provided that the ditch is built in soil rather than rock. Grader efficiency drops significantly when cross sections of larger dimensions are required.
For flows larger than 60 cubic feet per second, the trapezoidal ditch is commonly specified. The flat bottom and midsection of this ditch can be excavated rapidly by a wheeled scraper, and the side slopes can be dressed back by subsequent passes of a road grader.
Smaller bottom widths can be provided using any of the previously mentioned items of construction equipment, including the road grader with its blade turned to a high angle. Production rates, however, will be much lower than those of the wheeled scraper.
Note that the 60 cubic feet per second guideline is flexible. If scrapers are not available to excavate a ditch carrying 100 cubic feet per second but a grader is, common sense dictates that the grader be used to construct an oversized V ditch rather than using low-production-rate equipment to construct a trapezoidal ditch.
The segmental-ditch shape results when explosives are used to create the ditch. This technique is often used when the terrain is too soft to support excavating math inery. Ditches cut by hand will often bear this shape as well.
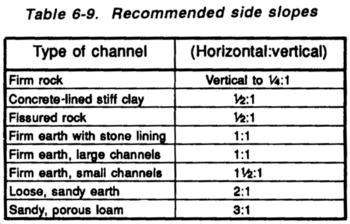
SIDE-SLOPE RATIOS
Ditches have two sides and two associated side-slope ratios. Side slope is the slope of the banks of the channels, normally expressed as a ratio of feet horizontal to feet vertical. For example, 3:1 is a side slope of 3 feel horizontal to 1 foot vertical. When the sidewalls on opposite sides are inclined equally, the ditch is called symmetrical. Nonsymmetrical ditches have side slopes that differ.
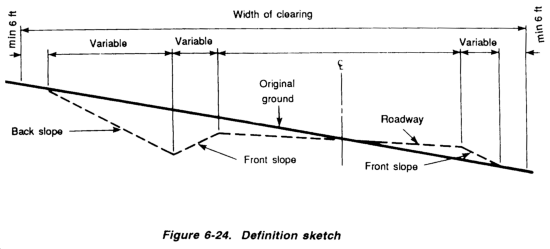
The designer selects appropriate side-slope ratios. The selection is critical to ensure that the ditch serves its purpose. Ditch sidewalls that are too steep invite excessive erosion and are likely to cause the ditch to clog with sediment. Even more serious is the risk of a severe accident, if a vehicle should run into the ditch and become entrapped or overturn because the side slope is too severe. Only one side slope is required for symmetrical ditches. For clarity, the terms front slope or ditch slope and back slope are used to differentiate between the dissimilar slopes. Figure 6-24, illustrates this terminology.
The sidewall of a roadside ditch located adjacent to the shoulder is called the front slope of the ditch. The far slope, called the back slope, is simply an extension of the cut face in an excavation. The following rules of thumb are applicable only in shallow ditches in relatively flat terrain:
- Roadside ditches may be cut nonsymmetrically at 3: 1/1:1 (front slope/back slope).
NOTE: For calculation purposes, the horizontal component of the roadside ditch will be referred to as X. Likewise, the horizontal component on the back slope will be referred to as Y. (See Figure 6-23.)
- Diversion ditches may be cut symmetrically at 1:1.
- Ditches intended to be subject to cross traffic may be cut symmetrically at 3:1 or more gently.
In most cases, interceptor and diversion ditches are installed far enough from the traveled way not to present a hazard to passing vehicles on the roadway or aircraft on the runway. Since there is very little danger from either side, symmetrical side-slope ratios are specified for these types of ditches.
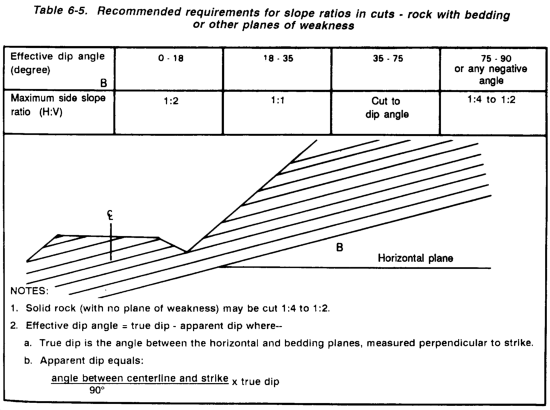
Tables 6-4 and 6-5 are also useful in selecting front slopes for fill sections.
TYPES OF FLOW
Several types of flow are associated with open channels. Some of these types occur simultaneously in the same channel. An understanding of these types of flow and their interrelationship is essential to the effective design of drainage systems.
An open-channel flow has a free surface and no hydraulic pressure. Some examples of open-channel flow include ditches, canals, streams, and culverts not flowing full. Empirical formulas with experimentally derived coefficients are used in designing an open channel. These hydraulic formulas reflect certain hydraulic theories and assumptions governing design analysis of free-flow channels.
A steady flow is assumed in an open channel with a uniform depth during the design period. Changes in flow are generally slow, and any errors that may be introduced by this assumption are not significant.
A continuous flow is assumed according to the principle of the conservation of mass.
A uniform flow is assumed when the depth of water throughout a channel is constant in dimension and slope. This means that the slope of the water surface is the same as the slope of the channel bottom. This assumption is essentially correct for channels of moderate slope and length. Flows in ditches, canals, and rivers are uniform, but flows over spillways or waterfalls are not uniform.
The strength of viscosity forces and hence the thickness of moving fluid, determine whether channel flow is turbulent or laminar.
Turbulent flow is assumed for purposes of open-channel design. This type of flow occurs when viscosity forces are relatively weak and the individual water particles move in random patterns within the aggregate forward-flow pattern.
Laminar flow occurs when viscosity forces predominate and the particles of the fluid move in smooth, parallel paths. An example of this type of flow is honey poured from a container; honey has high-viscosity strength compared to water. The only type of laminar flow considered in this manual is sheet flow, which occurs where depth is extremely shallow. It is assumed that the flow in natural and designed channels will be steady, continuous, uniform, and turbulent.
DESIGN EQUATIONS FOR OPEN CHANNELS
This section deals with open-channel design equations. Because of the variables and assumptions to be made, trial techniques are required to determine the shape and depth of a particular channel before a final solution is reached.
Continuity Equation
The equation of continuity is expressed as follows:
 = AV
= AV
where--
 = rate of flow in cfs
= rate of flow in cfs
A = cross-sectional area in sq ft
V = velocity in fps
Manning's Velocity of Flow Equation
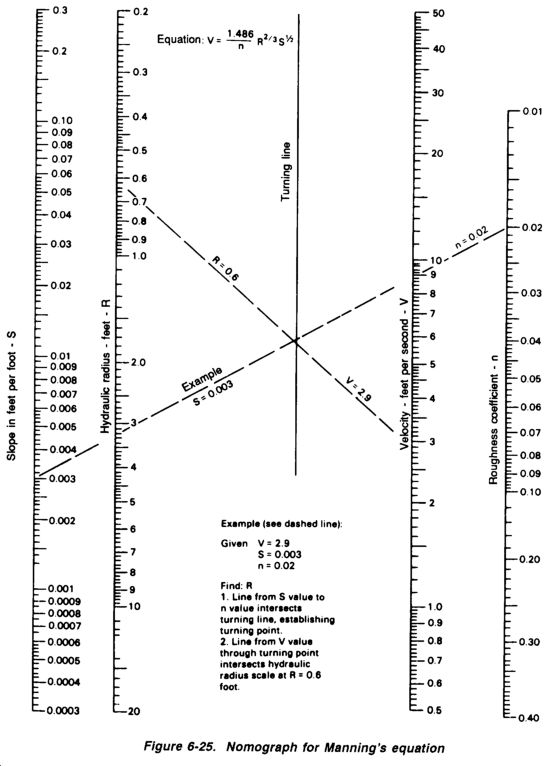
Many empirical equations have been proposed for determining turbulent flow. The most widely used is the equation presented by Manning in 1889. It states--
Manning's equation can easily be solved mathematically using the equation. However, to assist in the design of open channels, the equation has been prepared as a nomograph. (See Figure 6-25.)
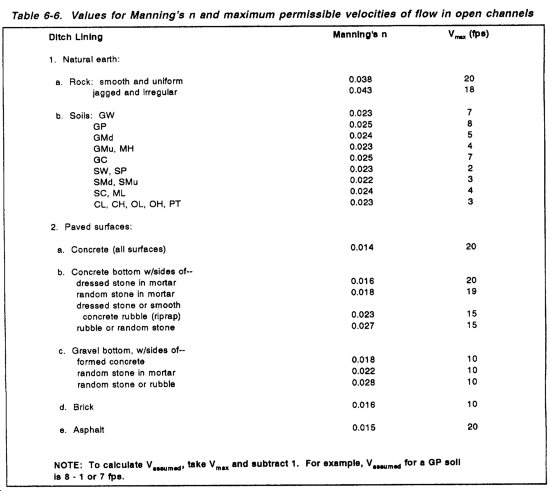
Roughness Coefficient (n)
The roughness or resistance coefficient is a measure of the resistance to flow caused by surface-contact irregularities. It varies with soil type, channel condition, and type of ditch lining used. Use Table 6-6 to estimate the roughness coefficient, n, used in the solution of the equation. The coefficient can be changed only if the ditch lining is changed or modified. The effect of the roughness coefficient on velocity can be altered by changing the side slopes of the ditch, thereby changing the water con tact area. Changing the roughness coefficient in this way changes the ditch capacity.
Longitudinal Slope or Grade (S)
Under normal conditions, the ditch slope (the longitudinal fall of the channel in feet per foot or in percentage) will be determined by the slope of the terrain. For short ditch lengths only, a variation from the natural slope of the terrain can be achieved by modifying the cutting depth of the ditch. By varying the cutting depth within the ditch length, the slope can be increased or decreased independently of the terrain slope.
In channel design, slope percentage and the resulting change in velocity are important considerations. Slopes over 2 percent may have too high a velocity, resulting in erosion. Slopes under 0.5 percent will generally have too low a velocity, resulting in sedimentation deposits. Deposition (the depositing of sediment on the bottom of the ditch) normally occurs at velocities below 3 feet per second.
Velocity of Flow (V)
Many ditches with differing side slopes and cross-sectional areas of flow will carry the same rate of runoff on a similar longitudinal slope. In each case, however, the velocity of flow will be different. Since excessive velocity in a ditch will cause erosion and possibly damage adjacent structures, it must be contained within limits. Table 6-6 lists the maximum permissible velocities, depending on soil and other factors.
Velocity Relationships
- As slope increases, velocity (V) increases.
- As quantity of runoff (Q) increases while area (A) remains constant, velocity (V) increases.
- If Manning's n increases, velocity (V) decreases.
- If velocity (V) increases, erosion increases.
Hydraulic Radius (R)
The hydraulic radius (R) is the area of the water cross section of the ditch divided by its wetted perimeter, calculated as shown in Figure 6-26. It relates the surface area of friction resistances with the volume of water being carried by the ditch. The hydraulic radius can be calculated using an electronic calculator as shown in Figure 6-27.
DESIGN CONSIDERATIONS
There are certain factors known for each ditch being designed. Each of these factors will affect design details. Items such as the location, the peak flow or runoff carried, the effect of terrain on slope, and the soil type or material to be used to line the ditch all have a bearing on channel design.
LOCATION
The location of the ditch will determine its general shape and the side slopes to be used in its design.
QUANTITY OF RUNOFF (Q)
Designers must know the quantity of runoff the channel will have to carry. Usually, this is estimated using the rational method of runoff determination. However, it may also be estimated based on knowledge of the slope, the diameter, and the type of culverts used to discharge into the channel. The value of Q will also determine which type of ditch section, triangular or trapezoidal, will be used. This depends on whether Q is greater than or less than 60 cubic feet per second.
SLOPE (S)
The slope will be determined by the terrain. In general, the slope used will be the natural ground slope. Small modifications of the slope can be made for short ditch sections.
PROPOSED DITCH LINING
The ditch lining determines the velocity and roughness coefficient or resistance factor, n. (See Table 6-6.)
Table 6-6 gives maximum erosion velocities for each type of soil and lining. The lower velocity on the chart indicates the velocity at which erosion will start occurring in some portion of the ditch. At the high velocity value, the entire length of the ditch will probably be eroding.
Table 6-6 also provides Manning's roughness coefficient (n) which represents the friction resistance of the ditch, channel, or stream for various soil types and linings. Use the average value of n for design purposes.
DESIGN TECHNIQUES
Once design considerations have been examined, the interactive design procedure can begin.
DESIGN STEPS
The steps used in design follow:
Step 1. Determine the peak volume of storm-water runoff,  . Calculate the total area(s) contributing flow to the ditch. (Use the rational method.) Using the appropriate formula, find
. Calculate the total area(s) contributing flow to the ditch. (Use the rational method.) Using the appropriate formula, find  .
.
Step 2. Determine the slope, S, in feet per foot. If the slope is already known as a percentage, it may be converted to units of feet per foot by simply dividing by 100.
Step 3. Select trial values for resistance, n, and velocity, V. From Table 6-6, select a value of the resistance or roughness coefficient, n, and a velocity, V, for the soil type in which the ditch is to be constructed.
The initial trial velocity should be held to 1 feet per second below the high value. Usually, the channel will be carrying less than design flow, reducing the velocity and making sedimentation likely. If a high value is chosen for the design velocity, this deposited material will be removed by the water during a peak flow without causing extensive damage to the channel.
Step 4. Determine the hydraulic radius. From the slope, S; Manning's n; and the velocity, V; find the hydraulic radius of the ditch, using the nomograph or equation.
Call this Rm to distinguish it from the R values in Appendix C of this manual, which will be Rt.
Step 5. Determine the type of ditch cross section. Where  is greater than 60 cubic feet per second, use a trapezoidal ditch. Where
is greater than 60 cubic feet per second, use a trapezoidal ditch. Where  is equal to or less than 60 cubic feet per second, use a triangular ditch. Whether the ditch is symmetrical or nonsymmetrical will depend on the specific location.
is equal to or less than 60 cubic feet per second, use a triangular ditch. Whether the ditch is symmetrical or nonsymmetrical will depend on the specific location.
Step 6. Select the appropriate hydraulic radius and area table. From Appendix C, select the appropriate hydraulic radius and area table for the desired ditch cross section. Identify the column headed with the tentative side-slope ratios. Enter the Rm table, locating the value of Rt that corresponds with Rm. Then find the cross-sectional area and ditch depth corresponding to Rm and Rt. In using the tables, if the Rm exact value is not available, use the next smaller Rt value listed in that column.
Step 7. Calculate  . Use the equation
. Use the equation  = AWV, where area, Aw, and velocity, V, are determined in steps 6 and 3, respectively. If the calculated
= AWV, where area, Aw, and velocity, V, are determined in steps 6 and 3, respectively. If the calculated  from step 7 is not more than 5 percent greater than the design
from step 7 is not more than 5 percent greater than the design  , the ditch selected can be used. If the calculated
, the ditch selected can be used. If the calculated  is more than 5 percent greater than the design
is more than 5 percent greater than the design  , reduce the velocity and repeat steps 4, 5, 6, and 7.
, reduce the velocity and repeat steps 4, 5, 6, and 7.
If the calculated  is smaller than the design
is smaller than the design  by more than 5 percent, increase the velocity. However, do not make it any larger than the maximum for the soil or lining based on Table 6-6. If the calculated
by more than 5 percent, increase the velocity. However, do not make it any larger than the maximum for the soil or lining based on Table 6-6. If the calculated  is still less than the 95-percent limit, the cross section must be increased by flattening the side slopes or by increasing the bottom width (if a trapezoidal section is used).
is still less than the 95-percent limit, the cross section must be increased by flattening the side slopes or by increasing the bottom width (if a trapezoidal section is used).
Step 8. Provide freeboard. Add 0.5 foot to the water depth to provide freeboard. Freeboard is the additional ditch depth over that required to carry the design flow. This added depth allows the ditch to carry the design capacity, even with sediment in the ditch bottom. The total depth, including freeboard, will be the cutting depth and the depth at which the ditch grade will be set.
Example:
Design a ditch to carry a peak volume of storm-water runoff equaling 47,3 cfs from a culvert to a stream that is 289 feet from the outlet of the culvert. The ditch invert (or bottom) elevation at the outlet of the culvert will be 7.0 feet above sea level. The ditch invert will be constructed above the stream high watermark at an elevation of 5.5 feet above sea level. The ditch lining will be the bare (unturfed) GMd soil, as excavated.
|
Soil (GMd): V |
= 3 to 5 fps (Table 6-6) |
|
|
= 0.024 (Table 6-3) |
Solution (Nomograph and Table Method):
The solution of a ditch problem is always a trial technique in which several values of velocity are used. Tables are recommended to tabulate the results. The tables should be similar to the ditch design work sheet shown in Table 6-7.
Step 1. Select a ditch. Since design flow,  , is less than 60 cubic feet per second, the ditch should be triangular. The channel is not a roadside ditch, so it should be symmetrical. Select side slopes for a 3:1 triangular ditch for the first trial. (This assumes that periodic vehicular crossings are expected.) These factors can be changed if the ditch design is not suitable. Enter the information in the columns under ditch selection on the ditch design work sheet.
, is less than 60 cubic feet per second, the ditch should be triangular. The channel is not a roadside ditch, so it should be symmetrical. Select side slopes for a 3:1 triangular ditch for the first trial. (This assumes that periodic vehicular crossings are expected.) These factors can be changed if the ditch design is not suitable. Enter the information in the columns under ditch selection on the ditch design work sheet.
Step 2. Select the velocity. The erosion velocity for the soil is 3 to 5 feet per second. This means that at 3 feet per second the soil in the ditch may begin to erode, and at 5 feet per second the whole ditch will be eroding. Since it is preferable not to exceed the Vmax of 5 feet per second, the best initial choice is usually 1 feet per second lower than Vmax or 4 feet per second. Enter this figure on the design work sheet.
Step 3. Determine the hydraulic radius, from the nomograph. Using the nomograph (Figure 6-26), first locate a turning line. The line is in the center on the nomograph. Find the turning point by locating the slope, S (in feet per foot), in the left column of the chart and the roughness coefficient, n, in the right column. Draw a straight line to connect the two points. The point at which the new line crosses the turning line is the turning point. This turning point will remain (he same as long as neither S nor n changes. The hydraulic radius, Rm, is found by connecting the velocity (in the second column from the right) and the turning point by drawing a straight line through to the R scale. Then read the hydraulic radius (R) in the second column from the left. This gives the required R for any given V in Manning's equation. In this example, R = 0.86. Enter this value on the work sheet.
The R value can be computed by using the calculator method shown in Figure 6-27.
Step 4. Find the hydraulic radius, in the ditch table. Locate the appropriate table among Tables C-2 through C-10 in Appendix C of this manual. There are four types of tables: V-triangular or symmetrical, V-triangular or nonsymmetrical, trapezoidal-symmetrical, and trapezoidal-nonsymmetrical. For this example, use Table C-2 for a symmetrical V ditch.
Locate the pair of columns representing the side slopes of the ditch being designed (for example, 3:1). Locate the Rt values that fall above and below, or the one that is exactly equal to, the Rm value found from the nomograph of Manning's equation. In this example, the Rm = 0.86 cannot be found in these columns, but the values 0.85 and 0.90 are given. Use the lower value (0.85) on the work sheet.
Step 5. Record the area and depth. With Rt = 0.85, the corresponding area found in Table C-2 is 9.72 square feet, and the depth (d) found in the column at the far left is 1.8 feet. Record these values under the appropriate headings on the ditch design work sheet.
Step 6. Check for  . Check to see if this particular ditch will meet the requirements of the design by performing the calculations--
. Check to see if this particular ditch will meet the requirements of the design by performing the calculations--
 = AwV
= AwV
 = (9.72 sq ft)(4.0 fps)
= (9.72 sq ft)(4.0 fps)
 = 38.9 cfs
= 38.9 cfs
This calculated quantity of flow ( ) must fall within 5 percent of the design flow of 47,3 cubic feet per second, or between 44.9 and 49.7 cubic feet per second. If this requirement is not met, as in this case, try a new velocity. If the calculated
) must fall within 5 percent of the design flow of 47,3 cubic feet per second, or between 44.9 and 49.7 cubic feet per second. If this requirement is not met, as in this case, try a new velocity. If the calculated  is less than 95 percent of the design flow, use a higher velocity. For this example, since 38.9 is less than 44.9 cubic feet per second (the lower limit of the acceptable range), a velocity of 4,5 feet per second would be an acceptable assumption for the next trial.
is less than 95 percent of the design flow, use a higher velocity. For this example, since 38.9 is less than 44.9 cubic feet per second (the lower limit of the acceptable range), a velocity of 4,5 feet per second would be an acceptable assumption for the next trial.
V = 4.5
Rm = 1.0
Rt = 0.95
Aw = 12.0 sq ft. d = 2.0 ft
 = (4.5 fps)(12.0 sq ft)
= (4.5 fps)(12.0 sq ft)
 = 54.0 cfs, which exceeds 49.7 cfs, so the next trial velocity must be less than 4.5 fps: try 4.2 fps.
= 54.0 cfs, which exceeds 49.7 cfs, so the next trial velocity must be less than 4.5 fps: try 4.2 fps.
V = 4.2
Rm = 0.92
Rt = 0.90
Aw = 10.83 sq ft, d = 1.9 ft
 = (4.2 fps)(10.83 sq ft)
= (4.2 fps)(10.83 sq ft)
 = 45.5 cfs
= 45.5 cfs
 is greater than the lower limit of 44.9 and less than the high limit of 49.7. This ditch is within the range and thus meets the ditch water depth and velocity requirements. Enter this value of
is greater than the lower limit of 44.9 and less than the high limit of 49.7. This ditch is within the range and thus meets the ditch water depth and velocity requirements. Enter this value of  on the ditch design work sheet.
on the ditch design work sheet.
Step 7. Determine if the ditch is appropriate. This process describes a symmetrical, triangular ditch in GMd soil, with a slope of 0.0052 feet per foot and 3:1 side slopes. It carries 45.5 cubic feet per second runoff with a water depth of 1.9 feet and a velocity of 4.2 feet per second.
Since the velocity in the ditch is greater than 3 fps, the ditch can be considered self-cleaning and requires little maintenance. Peak runoff will remove any silt buildup from the channel bottom. With V = 4.2 feet per second, there may be some erosion of the ditch, but it should not be a significant maintenance problem. The shape, lining, and slopes are acceptable.
Step 8. Determine the cutting depth. The water level in the ditch should be at least 0.5 foot below the edge of the ditch as a safety factor. Accordingly, the cutting depth is the water depth plus 0.5 foot of freeboard.
Cutting depth = d + freeboard
Using the rutting depth just calculated.
|
Cutting depth |
= 1.9 + 0.5 |
| = 2.4 ft |
Since there are 2.5 feet (8.0 - 5.5 = 2.5) of available cutting depth at the end of the ditch, the design is acceptable.
Conclusion: Use this ditch.
Alternative Solution (Calculator Method):
If it is more convenient to use the calculator method than the nomograph, the following procedure is used:
Step 1. Select a ditch. As before, the ditch is V-type and symmetrical. Assume side slopes of 3:1 have been selected for the trial cross section.
Step 2. Select the velocity. The assumed trial velocity should always be 1 feet per second less than the maximum erosion velocity of the soil. In this case, it will be 4 feet per second.
Step 3. Determine the hydraulic radius, Rm.
where--
V = 4 fps
n = 0.024
S = 0.0052 ft/ft
Step 4. Determine the area of water, Aw, and depth of water, d. As explained in Figure 6-28--
Aw = ½(xd + yd)d for any triangular ditch.
For this problem, x = 3, y = 3
|
Aw |
= l/2(3d + 3d)d | |
| = l/2(6d)d | ||
| = 3d2 |
The wetted perimeter (wp), as explained in Figure 6-29, is--
Wp = Cl + C2 = (xd)2 + d + (yd)2 + d
Substituting values of x and y--
Therefore, the hydraulic radius (Rm) is--
For depth (d), the depth of water for the conditions assumed in step 3, is calculated. Since Rm = 0.848 from step 3, and Rm is also equal to 0.474d, the depth of water (d) can be computed.
This allows Aw to be computed.
Aw = 3d2 = 3(1.79 ft)2 = 9.61 sq ft
Step 5. Check for  .
.
 = AwV = 9.6(4) = 38.4 cfs
= AwV = 9.6(4) = 38.4 cfs
The  calculated for the ditch must be within ± 5 percent of the design
calculated for the ditch must be within ± 5 percent of the design  of 47.3 cfs, or between 44.9 and 49.7. The calculated ditch
of 47.3 cfs, or between 44.9 and 49.7. The calculated ditch  is 38.4, which is less than the lower limit and is unacceptable. Since the calculated
is 38.4, which is less than the lower limit and is unacceptable. Since the calculated  is below the lower limit, raise the velocity for the next trial calculation. For the second trial, the assumed velocity will be 4.5 feet per second.
is below the lower limit, raise the velocity for the next trial calculation. For the second trial, the assumed velocity will be 4.5 feet per second.
Step 6. Make a second trial calculation.
 is too high; try V = 4.2 fps.
is too high; try V = 4.2 fps.
Step 7. Make a third trial calculation.
 is acceptable, because it is between the limits.
is acceptable, because it is between the limits.
Step 8. Determine the ditch. With the  being acceptable, the ditch will have a water depth of 1.92 feet and side slopes of 3:1. Additional depth must be added to the water depth for freeboard. This additional depth can be selected depending upon the conditions external to the ditch but cannot be less than 0.5 foot. Therefore--
being acceptable, the ditch will have a water depth of 1.92 feet and side slopes of 3:1. Additional depth must be added to the water depth for freeboard. This additional depth can be selected depending upon the conditions external to the ditch but cannot be less than 0.5 foot. Therefore--
| Cutting depth | = water depth (d) + 0.5 |
| = 1.92 + 0.5 | |
| = 2.42 ft or 2.4 ft |
The velocity of 4.2 feet per second is acceptable. Some erosion may be anticipated, but it will not be serious. In addition, because of the high velocity, the flow will clean out the sediment from previous low flow.
SPECIAL CHANNELS
Some facilities will have special types of channels where surface runoff will be intercepted and removed. These channels will be similar to open channels, except they will tend to be very wide and shallow. To determine runoff capacity (in cfs) in this type of channel, open channel hydraulics, as previously discussed, must be modified.
Gutters
Gutters are shallow, paved drainage channels used in more permanent construction adjacent to paved or hard-surfaced areas. They provide positive removal of runoff, protection for easily eroded soils adjacent to the pavement, and prevention of softening of turf shoulder areas commonly caused by a large volume of runoff from adjoining pavements.
A cross section of a typical runway gutter is shown in Figure 6-30. This gutter conforms to US Air Force safety requirements and design charts of that particular gutter. Safety and operational requirements for fast landing speeds make it desirable to provide a continuous, longitudinal grade in the gutter. Close conformity to the runway gradient requires the use of sump inlets (drop inlets covered by gratings). A sufficient number of inlets should be provided in the gutter to prevent the depth of flow from exceeding 3 inches.
Median Channels
Channels will be placed down the center of medians, dual roads, runways, taxiways, and other similar structures. These channels will be symmetrical but very wide and shallow. The input flow into such channels is from surfaced and unsurfaced areas adjacent to the channel. The flow can be determined by the rational method. Since the factors of slope (S), Manning's n, flow ( ), and the general width are known, the depth can be determined by trial using the flow equation or nomograph for flow in open channels.
), and the general width are known, the depth can be determined by trial using the flow equation or nomograph for flow in open channels.
BERMS
The uncontrolled inflow from drainage areas adjacent to open channels has been a source of numerous erosion failures. Combating this problem requires special consideration during the design of the surface drainage system. Local runoff inflow can be particularly detrimental. Because of normal irregularities in grading operations, runoff becomes concentrated and causes excessive erosion as it flows over the sides of the channel. Experience shows that constructing a berm (raised lip), Figure 6-31, prevents this problem. Place the berm, usually made of earth, at the top edge of the channel. This berm prevents inflow into the channel except at designated points where an inlet, properly protected against erosion, is provided.
Where excavated material is wasted, as in a levee or dike parallel to the channel, there must be frequent openings through the levee to permit inflow to the channel. A suitable berm allows a minimal amount of excavated material to flow back into the channel. This prevents sloughing from the spoil bank into the channel.
Runoff,  , from the area is determined by the rational method. This runoff is collected and conveyed by the channel formed by the berm. The factors of
, from the area is determined by the rational method. This runoff is collected and conveyed by the channel formed by the berm. The factors of  , n, S, and width are used to solve for depth by the trial method.
, n, S, and width are used to solve for depth by the trial method.
CONSTRUCTION AND MAINTENANCE OF CHANNELS
Ditch construction normally requires either a grader or a scraper. Sometimes, these two items are used in combination. Depending on the location, other factors must be considered in designing and building ditches.
Interceptor ditches should be set on grades, thus allowing for quick removal of water without erosion. When the grade is not sufficient to permit quick water removal, the ditch may require an asphalt or concrete lining. Berms may be constructed on the downhill side of interceptor ditches, as shown in Figure 6-31, to prevent overflow and excessive erosion of the downhill slopes.
Abrupt changes in a ditch's normal flow pattern will induce turbulence and cause excessive erosion. These conditions develop most frequently at channel transitions, junctions, and storm drain outlets. Accordingly, special attention must be given to these locations during design.
Channel maintenance problems exist in all drainage systems. The basic design of the ditch must consider these maintenance problems before they arise. Therefore, designers must have a thorough understanding of the two basic ditch maintenance problems: sedimentation and erosion. Channel protection and ditch shape, when used together, control maintenance problems most effectively.
SEDIMENT CONTROL
Water flowing overland tends to carry sediment into any open channels. When the velocity in the channel is 3 fps or less, this sediment can be deposited in the channel. Since most storms are less intense than the design storm, the channel bottom may accumulate a large volume of loose sediment. When peak flow does occur, the velocity should be great enough to scour the channel bottom clean of loose sediment. If the sediment is not removed, it will compact and gradually reduce the depth of the ditch. At peak flow, the ditch may overflow and cause damage to adjacent structures before the channel is cleaned out; therefore, the channel should be kept clean through maintenance.
When designing channels, keep peak velocity flow above 3 fps. This keeps the channel self-cleaning. A higher velocity is preferred, but such velocity must not exceed the maximum velocity for the soil. (See Table 6-8.) When the soil type requires a maximum allowable velocity under 3 fps, sedimentation will be a maintenance problem. One solution is to line the ditch with asphalt or concrete. This reduces the coefficient of friction, thus increasing the velocity. When sedimentation is expected and linings cannot be used, increase the allowable freeboard to eliminate overflow.
EROSION CONTROL
Water flowing through open channels is turbulent. This turbulence increases as the velocity increases. Together, velocity and turbulence erode and carry away the soil of the channel and endanger nearby structures such as roads, bridges, and culverts. Velocity and turbulence may also endanger the channel itself. In addition, the eroded material may sometimes be deposited within the channel in areas where it will cause damage. In these cases, channel maintenance and repair will be a constant concern.
Erosion most commonly occurs when the velocity of flow exceeds the velocity at which the soil of the channel will erode. Table 6-8 shows the maximum velocities. Erosion can be prevented by lowering the velocity below the soil-erosion velocity. This can be accomplished by lining the natural channel material with a more erosion-resistant material or by reducing the side slopes. Table 6-9 shows the recommended side slopes. Erosion should be considered and accounted for in the design of channels.
Decreasing the Hydraulic Radius
Reducing the hydraulic radius will decrease the velocity. This decrease in hydraulic radius can be accomplished by increasing the wetted perimeter, wp, in relation to the area, A (while the  remains constant). This can be done by widening the ditch, flattening the side slopes, or widening the bottom. This increases the wetted perimeter without materially increasing the area. The required changes in ditch design are determined by the trial approach, since the amount of runoff,
remains constant). This can be done by widening the ditch, flattening the side slopes, or widening the bottom. This increases the wetted perimeter without materially increasing the area. The required changes in ditch design are determined by the trial approach, since the amount of runoff,  , must be retained while reducing the velocity.
, must be retained while reducing the velocity.
Lining the Channel
Erosion can be controlled by lining the bottom and sides of the channel.
Grass or Turf
Since natural linings take considerable time to grow or effort to place, they are seldom used in the TO.
Riprap
Riprap lining involves placing rocks or rubble in the bottom and on the sides of the ditch to prevent soil erosion. Rocks should be hand-placed in at least two layers and compacted individually. Riprap not only prevents erosion but decreases velocity in the channel because of its high n value. Riprap also helps prevent erosion when making transitions from paved to soil ditches or from other high-velocity ditches to those in which lower velocity is required. Gabions are another method of lining ditches. Details on riprap and gabions are given below.
Pavement
When the design and construction are done properly, paving the ditch with asphalt or concrete will prevent erosion. Because of the low n values of different types of pavement, velocity may increase too much, causing erosion where the pavement ends. Special protection, such as a stilling basin or rock lining, may be required at this point to slow the velocity before allowing the flow to continue into the natural soil channel. Because of pavement's low n values, it can be used effectively to increase flow velocities if they are too low, thus preventing deposition.
Installing Check Dams
The water velocity in a channel can also be reduced by decreasing the slope. However, except for local variations, building ditches at slopes other than that of the surrounding ground is impractical. One method for decreasing the slope is to install check dams or weirs, as shown in Figure 6-32. Check dams should be considered when the slope ranges between 2 and 8 percent. Channels with slopes of 2 percent or less generally do not require extensive erosion controls. With slopes in excess of 8 percent, it is usually more economical to pave the ditch with asphalt or concrete than to build check dams.
Design
Correct spacing between check dams can be determined by using the following formula:
where--
S = spacing, in feet, between check dams (This value should not be less than 50 feet.)
H = height from the channel bottom to the lower edge of the weir notch (This value should not be greater than 3 feet unless the dam is to be structurally designed. To prevent unnecessary work, the practical lower limit for H is 1 foot.)
A = slope of the original ditch in percent
B = desired slope in percent (This value should be set at 2 percent. This is the maximum slope that will not require additional erosion control.)
Example:
Original slope = 5%
Desired slope = 2%
H = 3 ft
Find S.
The spacing between check dams is 100 feet. To prevent erosion of the sides of the channel at the check dam, a weir notch is built in the center of the dam. The weir notch must be designed to carry the flow in the ditch. Weir-notch dimensions for various flow rates are given in Table 6-10.
Maintenance
Erosion is a common problem with check dams. It usually occurs when the weir notch is too small or is clogged with debris so that water flows over the top of the dam. Scour begins on the area exposed to the hydraulic jump. If allowed to continue long enough, the erosion will extend to the area around the dam, as seen in Figure 6-33. If this occurs, there will be more damage caused to adjacent structures than if the dam had never been installed.
Some protection usually takes the form of an extended horizontal or sloping apron. Scour can also be prevented by anchoring the sides and bottom into at least 2 feet of compacted material. Then place riprap along at least 4 feet of the downstream channel. These construction techniques will prevent scour and undercutting.
SECTION III. CULVERTS
A culvert is an enclosed waterway used to pass water through an embankment or fill. The flow in a culvert depends upon several factors, including the lining, slope, headwalls, wing walls, and downstream conditions. Accordingly, culvert types and construction procedures are discussed prior to considering culvert hydraulics and design features.
CULVERT TYPES AND DESIGNS
PERMANENT CULVERTS
Permanent structures can be constructed from corrugated metal pipe (CMP), concrete multiplate pipe arch, vitrified clay (VC), polyvinyl chloride (PVC), or other material.
Corrugated-Metal-Pipe Culverts
Because it is commercially available in numerous shapes, lengths, and diameters, CMP is commonly used in military construction. For TO construction, CMP is made of an aluminum-and-steel alloy. It comes in nestable half sections that, when assembled, give 2-foot effective lengths. It is available in the diameters and gages listed in Table 6-11. The minimum diameter recommended is 18 inches for lenghts up to 20 feet and 24 inches for all other lengths. Small diameters may become clogged with debris and are difficult to maintain.
Specific construction techniques are employed in placing CMP. A retaining wall called a headwall is placed at the upstream end of the culvert. Headwalls are always used upstream; they are desirable but not mandatory for the downstream end. The headwall supports the soil mass at the end of the culvert and helps to protect against erosion.
CMP joints must be lapped so that water flowing through the culvert passes over the joint rather than into it. Failure to properly overlap the pipes will tend to force the flowing water through the joints and into the fill. All joints must be sealed, preferably with caulk or bituminous material. If joints are not sealed, voids may be generated around culverts, causing collapse of the fill. To increase the velocity for a greater quantity of flow, line the culvert with asphalt. Commercial CMP is available with asphalt linings.
Assembling Nestable CMP
CMP has flange-type fittings which are easily fastened together by nuts and bolts that come with the sections. Vise grips and a ratchet set make assembly faster and easier.
Concrete-Pipe Culverts
When available, precast concrete pipe should be used instead of CMP for culverts. It has two advantages over CMP. First, it is stronger and requires less cover than CMP to support the same load. Second, the interior surface of concrete pipe is smoother (Manning's n = 0.013) than CMP (Manning's n = 0.024). Because of these advantages, concrete pipe of the same diameter and slope as CMP will carry a higher flow.
Concrete pipe is fabricated in circular and noncircular cross sections. It is available in many lengths and widths. Seal joints between the sections to prevent excessive leakage and subsequent weakening of the fill section Substantial headwalls are required at both ends to prevent separation at the joints. Start assembly downstream and work upstream, ensuring male ends point downstream.
Concrete-Box Culverts
Consider concrete-box culverts where the full area of the waterway must be used. One advantage is that the box can be designed to withstand external loads with little or no cover. Box culverts are especially adaptable to rock sites, since the bottom of the culvert can be placed directly on the rock.
Concrete-box design requires knowledge of construction techniques for reinforced concrete structures. Box culverts can be precast, but construction in the TO will probably require that they be cast in place.
EXPEDIENT CULVERTS
Expedient field-type culverts are built of material available on-site such as logs, oil drums, and sandbags filled with a sand-cement mixture. Some examples of culverts built of these materials appear in Figures 6-34, 6-35 and 6-36. Expedient culverts built and sized properly should serve until permanent structures can be built. For evaluating hydraulics, end areas equivalent 10 CMP can be used for similar slopes.
CULVERT CONSTRUCTION
Proper placement is one of the most important factors during culvert construction. It is a major contributor to survival of the culvert under adverse conditions. Some things to consider in placing culverts are culvert alignment: slope; fill placement; compaction under, around, and over the culvert; culvert length; and protection against erosion.
Alignment
The relationship of the culvert to the streambed is of major importance. Improper location can cause the stream to seek an alternative path other than the culvert. This could quickly close a road or airfield to traffic. To lessen this effect, use the alignment techniques shown in Figure 6-37.
To maintain an existing drainage pattern, place the culvert directly in the streambed, as in view (A) of Figure 6-37. Even though this may be diagonal to the fill, if the hydraulics of the channel are not changed, the stream will not change its direction.
Prevent the stream from shifting its course at the culvert inlet or outlet. Sometimes the structure will cut across a stream meander as in view (B) of Figure 6-37 This leads to doubt as to where to lay the culvert in the streambed. In this case, it is best to cut a new channel 10 lead the stream away from the structure. The old streambed must be filled and dammed with erosion-resistant material at the junction of the old and new channels. The dam can be built of sandbags, logs, riprap, or other similar material.
Provide a smooth transition into and out of the culvert. The structure may cut across a bend of the stream, as in view (C) of Figure 6-37, with a straight run of the stream through the structure. If the bend is close to the structure, it is preferable to recut the stream as shown, and lay the culvert in the new streambed. Care should be taken to fill in and dam the entrance to the old streambed and the junction of the two streambeds, as descibed above.
Move the water past the project as quickly as possible. When the channel flows parallel to the structure, erosion will eventually occur. To prevent erosion, dig a new channel routing the flow through the culvert and away from the structure, as shown in view (D) of Figure 6-37. Again, be sure to fill and dam the old streambed at the junction point.
The alignment of ditch relief culverts is shown in Figure 6-38. The amount of flow and the slope of the ditch determine the spacing between culvert inlets. On a road with a 5-percent grade, relief culverts should be spaced 500 feet apart. On an 8-percent grade, spacing should be reduced to 300 feet.
Slope
Culverts normally should be installed with the invert of both the inlet and the outlet of the culvert at streambed or channel elevation. The invert is the lowest point in the internal cross section of an artificial channel or the bottom of the culvert. The normal grade of the culvert can be modified by two techniques, as shown in Figure 6-39.
- Drop inlets can be used to lower the inlet of the culvert. This will tend to reduce the slope of the culvert. An example of a drop inlet is shown in view (A) of Figure 6-39 and a discussion later in this chapter.
- The outlet of the culvert can be raised to reduce the slope, as shown in view (B) of Figure 6-39.
For culverts to be self-cleaning, flow velocity should be at least 3 fps. To achieve this velocity, the culvert should not be set on less than a 0.5 percent grade, if practicable. To prevent excessive outlet velocity, the culvert grade should not exceed 2 percent.
In general, free-falling outlets and culverts with slopes of more than 2 percent will require outlet erosion protection. In mountainous country where there are excessive stream slopes or in fills across dry valleys, culverts may have to be set at grades other than the terrain or streambed slope. In the TO, it may be advisable to accept the erosion problem and install the culvert with a slope for an excess of 2 percent. This will help to prevent a blockage caused by debris passing through the pipe.
Depth of Fill
The distance measured from the culvert invert to the edge of the shoulder or top of the fill, as shown in Figure 6-40, is the depth of fill. The depth of fill must be equal to or greater than the cover plus the pipe diameter. Otherwise, a smaller diameter culvert or a drop inlet must be used. For a road culvert made of CMP, the largest diameter allowable must equal two-thirds the minimum fill depth.
Cover
The depth of compacted soil from the top of the culvert (crown) to the finished construction grade is called cover. The culvert and the surrounding compacted soil must have sufficient strength to carry the compacted soil backfill (dead loads) and the wheel and impact loads (live loads) of the traffic. Live loads are more damaging than dead loads on culverts under shallow cover, and dead loads are more damaging than live loads on culverts under deep cover. Accordingly, both minimum protective cover and maximum permissible depths of backfill must be included in design considerations for culverts. During construction, provide adequate additional cover to protect the culvert from damage in places where heavy construction equipment will be crossing frequently.
The minimum cover required to protect the culvert pipe against live loads will depend upon the type of load. For road culverts, the minimum cover is one-half the diameter of the culvert, or 12 inches, whichever is greater. The cover over culverts used in airfields must be specifically designed for the heaviest aircraft using the facility. Table 6-12 lists characteristics of US aircraft. Use this table to determine the landing-gear configuration, wheel loads, and culvert weight type. This will, in turn, allow you to select the proper fill requirements category in Table 6-13, or Table 6-14.
Tables 6-13 and 6-14 give the cover requirements for culverts under airfields. These tables are composed of a series of charts based on aircraft load and gear configurations. Each of these charts is headed by a culvert weight type. These charts are good for 5,000 pounds more than listed. (For example, the chart headed "60,000-lb Singlewheel" is good for single-wheel loads up to and including 65,000 pounds.)
Each chart is subdivided into columns headed by culvert pipe diameters, in inches, and rows based on the gage of the metal. Use linear interpolation for the incremental diameters not listed. The body chart gives the cover required, in feet, for the diameter and gage of pipe concerned.
To use these tables, find the chart that applies to the particular aircraft wheel or gear load and landing-gear type. Then use Table 6-12 to find the appropriate culvert type. When the proper chart is located, read down the left column of the table to determine the appropriate row for the gage concerned. When the proper row has been found, read horizontally to the right and find the minimum cover, in feet, under the column headed with the pipe diameter in question. Two examples of this tabulation follow.
Example 1:
C130E Hercules--12-gage pipe; from Table 6-12, C130E requires culvert WT type 13.
60,000-lb single-tandem--12-gage pipe. (Use 60,000-lb single-tandem assembly (assy), chart 13.)
From chart:
Example 2: 60,000-lb single-wheel--8-gage pipe. (Use chart 5 in Table 6-13.)
The maximum permissible depth of fill (cover) for CMP is given in Table 6-15 for steel and Table 6-16 for aluminum alloy. Reinforced concrete pipe made under standard specifications can be used in fill up to50 feet.
Bedding (Foundations)
The minimum bedding depth for pipe culverts is one-tenth the diameter of the pipe as shown in Figure 6-40. The bedding is formed and shaped to fit the bottom of the culvert. In addition, the foundation is cambered (curved slightly upward), as shown in Figure 6-41 along the centerline of the culvert to allow for settlement and to ensure tightness in the joints. At no time should the invert elevation increase as the flow proceeds downstream.
Culverts are constructed on firm, well-compacted foundations. The composition of the soil on the bottom of the stream should be determined. Good granular material will be required to form a proper compacted and shaped bed. If a stream bottom is composed of poor material, such as organic matter, muck, silt, or large material that could puncture the CMP, remove and replace the material. The depth of material to be removed will depend upon information from borings. When the bearing strength of the soil is completely inadequate and uneven settlement is expected provide cradle footings. These footings may require piling as shown in Figure 6-42. Footings used for timber culverts as shown in Figure 6-43, can also be adapted for various types of culverts and soils.
Culverts can be placed on properly prepared rock foundations. Trench the rock and backfill with firmly compacted soil for bedding the culvert, as shown in Figure 6-44.
Backfill
Take care in backfilling around the culvert, since the backfill supports the culvert against soil pressure generated by surface loads as shown in Figure 6-39. The soil selected should be placed carefully in well-compacted layers kept at the same elevation on both sides of the culvert. Compaction is done in 6-inch layers if hand-or air-operated or if other mechanical tampers are used. If logs, hand tamping, or other expedient methods are used, place the soil in 4-inch layers. Carry the compaction from the culvert bed material to 12 inches or one-half the diameter above the top of the culvert (whichever is greater).
Length
Culvert length is determined by the width of the embankment or soil mass through which the culvert carries water. Culverts that do not include a downstream headwall must be long enough 10 extend a minimum of 2 feet beyond the toe of the embankment to prevent erosion.
Headwalls, Wing Walls, and Aprons
Headwalls and aprons are constructed to guide water into the culvert, prevent or control erosion, reduce seepage, hold the soil in place, and support the ends of the culvert. Headwalls close to roads should not protrude above the shoulder grade. They should be at least 2 feet outside the shoulder so they do not present a traffic hazard.
Use headwalls on the upstream end of all culverts. If possible, use a headwall on the downstream end as well. When concrete pipes are used, headwalls are mandatory at both ends. Headwalls, both upstream and downstream, should have wing walls or retaining walls set at an angle 10 the headwall. This will help support the fill and direct the water flow to prevent erosion. The upstream wing wall will guide the water into the culvert and assist in improving the culvert hydraulics. The downstream wing wall, combined with an apron, will help reduce the velocity of the stream, and thereby lessen erosion al the outlet Ideally, headwalls and wing walls should be reinforced concrete or mortared stone. Standard designs are in the TM 5-302 series manuals. They can, however, be made of expedient material such as lumber, logs, or sandbags. These structures are shown in Figure 6-45. For speedy construction in the TO, sandbags filled with a soil-and-cement mixture may provide the best headwall possible.
When headwalls are not used on the downstream end, the culvert should project beyond the toe of the fill at least 2 feet. Use riprap to protect the projecting area culvert riprap, as shown Figure 6-46.
Erosion Control
Culverts discharging into open channels should have antiscour protection to prevent erosion. Two types of channel instability can develop downstream from culvert and storm-drain outlets. These conditions, known as gully scour and scour hole, are shown in Figure 6-46. Predict the type of scour for a given field situation by comparing the original or existing channel slope or drainage basin downstream of the outlet to what is required for stability.
Gully scour is expected when channel flow exceeds that required for stability. It begins at a point downstream where the channel is stable and progresses upstream. If sufficient differential in elevation exists between the outlet and the stable channel, the outlet structure will be completely undermined. Erosion of this type may be considerable, depending on the location of the stable channel section relative to the outlet in both the vertical and downstream directions. View (A) of Figure 6-47 illustrates this condition.
A scour hole or localized erosion, as shown in view (B) of Figure 6-47, is to be expected if the downstream channel is stable. The severity of damage to be anticipated depends on existing conditions or those created at the outlet. In some instances, the extent of the scour hole may be insufficient to produce either instability of the embankment or structural damage to the outlet. However, in many situations, flow conditions produce scour that erodes the embankment and causes structural damage to the apron, end wall, and culvert. This type of outlet erosion of the bottom of the ditch and of the side banks is shown in Figure 6-48.
Erosion is best controlled by two methods: velocity reduction and channel protection. Reducing the slope of the culvert reduces the velocity. This solution, however, may require a larger pipe since it changes the capacity of the culvert.
Headwalls, wing walls, or channel linings can absorb the energy of flowing water and reduce its velocity to acceptable levels. When wing walls are not provided, line the stream bank and bottom for some distance downstream with riprap or other material. Ditch linings were described in greater detail earlier in this chapter.
CULVERT DESIGN
The hydraulic load on a culvert is the amount of water that will flow to the culvert inlet, either as direct surface or channel-stream flow. Surface flow is determined by the rational and channel-flow-equations methods discussed earlier.
Hydraulics of Culverts
Culvert quantity of flow ( ) is the amount of water the culvert will carry in a unit of time. This capacity is expressed in cfs. For a particular culvert of known size (A), shape, and interior roughness (n), the discharge capacity is controlled by one or more of the following factors:
) is the amount of water the culvert will carry in a unit of time. This capacity is expressed in cfs. For a particular culvert of known size (A), shape, and interior roughness (n), the discharge capacity is controlled by one or more of the following factors:
- Height of the water above the culvert inlet.
- Hydraulic gradient (S) of the culvert.
- Length (L) of the culvert.
- Elevation of the tailwater at the culvert outlet.
The type of inlet is not generally considered in military culvert design. However, it should be remembered that the discharge capacity of a culvert will be increased by a smooth, transition type of inlet with headwalls and wing walls. For construction in the TO, the culvert should have a design capacity sufficient to pass the peak runoff from the design storm.
Hydraulic Gradient
The hydraulic gradient (S) of a culvert is one of the culvert discharge capacity controls. It can be satisfactorily estimated as the slope in ft/ft. The gradient is calculated by dividing the head (H) on a culvert by the culvert length (L): S = H/L. The head is the difference in elevation between the following:
- The two ends of a culvert, if both the inlet and the outlet are not submerged.
- The water surface directly above the inlet and the top of the outlet, if the inlet is submerged and the outlet is not submerged.
- The water surface directly above the inlet and the outlet, if both the inlet and outlet are submerged.
The hydraulic gradient and head are illustrated in Figure 6-49.
The normal flow pattern for culverts, for which Table 6-17 is used, is shown by view (A) of Figure 6-49. In this case, the water is at crown elevation al the inlet, and the outlet is free-flowing.
An accumulation of water at the inlet of the culvert is called ponding. When pending occurs, the outlet will normally be free-flowing, but the water will be at some depth above the inlet. When this depth at the inlet is 1.2D or less (where D is the diameter of the culvert), use Table 6-17 to directly determine  and V. When the water depth at the inlet invert is greater than 1.2D and the outlet is free-flowing, use a nomograph (Figure 6-50) to determine
and V. When the water depth at the inlet invert is greater than 1.2D and the outlet is free-flowing, use a nomograph (Figure 6-50) to determine  , and use the continuity equation
, and use the continuity equation  = VA to determine the velocity.
= VA to determine the velocity.
When both the inlet and the outlet are completely submerged, use Figure 6-50 exclusively.
Critical Slope
For a given size, A, of the culvert and a given head, H, on the culvert, the discharge capacity of the culvert will increase as the hydraulic gradient increases. This continues until the hydraulic gradient becomes equal to or greater than the critical slope, Sc. As the hydraulic gradient is increased beyond the critical slope, culvert discharge remains constant. The area decreases because the pipe does not flow full, and the velocity of flow in the culvert increases because V =  /A. The critical slope is the maximum discharge.
/A. The critical slope is the maximum discharge.
Roughness
For the selection of the pipe roughness values (n values) for flow determination refer to the footnotes to Table 6-17.
Box-Culvert Flow
Flow characteristics of box culverts may be different from those of pipe culverts, even those with the same slope, lining, and inlet and outlet conditions. Flow,  , can be determined as previously noted, for the conditions of inlet and outlet water elevations.
, can be determined as previously noted, for the conditions of inlet and outlet water elevations.
Assuming that the water elevation of the inlet is at the top of the box and the outlet is free-flowing, the difference in inflow characteristics between pipe and box culverts of the same material and slope is negligible. Box-culvert sizes can therefore be determined by computing the cross-sectional area required for a pipe and then designing a box of the same material, slope and cross-sectional area.
When the water elevation is above the top of the box inlet, use the nomograph in Figure 6-50. In this case, make trial solutions until there is correlation between the box size and pending depth.
Design of Culverts with Submerged Inlets
Submerging of the culvert inlet results in pending at-the site. The elevation of the pond surface, which will determine the depth of submergence, is a function of the extent of the pond, the requirement of safety to the structure, and the time it will take to empty the pond. These factors are determined by the runoff rate, the pond volume, and the culvert-flow rate. They are derived using the following steps:
Step 1. Determine the rate of runoff ( ) the culvert must drain or, in the case of pending, the inlet drain capacity,
) the culvert must drain or, in the case of pending, the inlet drain capacity,  d.
d.
Step 2. Determine the length of the culvert.
Step 3. Determine the head on the culvert.
Step 4. Using Figure 6-49, determine the size and type of pipe or box culvert required to handle the quantity of flow,  .
.
To use this table, enter the nomograph (Figure 6-50) at the intersection of the length for the type and size of culvert (for example, point A in the nomography). Extend the line horizontally to the turning-point line (point B in the nomography), and extend the line to the culvert head, H, in feet (point C in the nomography). Find the discharge,  , in cubic feet per second, for the pipe selected at the intersection with the discharge line.
, in cubic feet per second, for the pipe selected at the intersection with the discharge line.
Step 5. Compute the discharge velocity, V, in fps. Use the equation, V =  /A. If the discharge velocity is greater than the maximum permissible velocity for the outfall or the height of the water, in feet, above the top of the culvert inlet is less than 0.022(V2) for CMP or 0.017(V2) for concrete pipe or boxes, either select pipes of larger diameter or decrease the slope of the culvert.
/A. If the discharge velocity is greater than the maximum permissible velocity for the outfall or the height of the water, in feet, above the top of the culvert inlet is less than 0.022(V2) for CMP or 0.017(V2) for concrete pipe or boxes, either select pipes of larger diameter or decrease the slope of the culvert.
Example (Submerged Inlet, Unsubmerged Outlet):
Determine the most economical pipe size and number of pipes required for a culvert across an airfield. The following are known conditions:
The outfall from the culvert is a natural drainage channel with dense turf in a GP soil.
- The design flow,
 , is 210 cfs.
, is 210 cfs. - 42-inch and 48-inch concrete pipes are available.
Solution:
Step 1.  = 210 cfs (given).
= 210 cfs (given).
Step 2. L = 180 feet (given).
Step 3. Determine head, H.
| H 42-in | = 598.6 ft - (593.0 ft + 3.5 ft) | |
| = 2.1 ft | ||
H 48-in |
= 598.6 ft - (593.0 ft + 4.0 ft) | |
| = 1.6 ft |
Step 4. Determine the size and number of pipes required to handle the flow,  .
.
(a) On the cast-concrete-pipe portion of the nomograph, draw a horizontal line from the intersection of the 180-ft L line and the 42-in pipe line (point A) to the turning-point line (point B). From B, draw a line to an H of 2.1 ft (point C). The intersection of this line with the " " portion of the nomograph shows the maximum discharge of one 42-in pipe to be about 78 cfs. For 210 cfs, three would be required.
" portion of the nomograph shows the maximum discharge of one 42-in pipe to be about 78 cfs. For 210 cfs, three would be required.
(b) Similarly, for the 48-in pipe, 180 ft length, and 1.6 ft H, proceed from D to E to F and find that one 48-in pipe would have a capacity discharge of about 92 cfs. Again, three would be required for 210 cfs.
Step 5. Compute the discharge velocity, V, and check for excessive outlet velocity. Check smaller pipe.
(a) Since three pipes are used, assume each will carry one-third the total  or 70 cfs, whichever is greater.
or 70 cfs, whichever is greater.
(b) If the pipe flows full, the exit velocity is--
(c) If the exit velocity is based on a design flow of 70 cfs, the pipe would be flowing only partially full and the exit velocity would be 9.2 fps. This velocity is greater than when the pipe flows full because the resistance to flow decreases until the pipe is flowing approximately 0.8 full.
(d) Check to see that H1 > 0.017(V2).
H1 = 598.6 ft - (594.0 ft + 3.5 ft) = 1.1 ft and 0.017 x 9.22 = 1.44
(e) Since allowable outfall velocity is exceeded and H1 < 0.017(V2), use three 48-inch pipes as the most economical available size.
Design of Pipe Culverts with Unsubmerged Inlets
The factors to be applied to the design of these culverts are determined as follows:
Step 1. Determine the rate of runoff. Use the area the culvert must drain. This will be the required capacity,  p, of the culvert.
p, of the culvert.
Step 2. Determine culvert use. Will it be used for a road or for an airfield?
Step 3. Calculate the critical dimensions from the cross sections. See Figure 6-51. Determine the length in place (LIP) and the fill critical (Fc).
Step 4. Determine the largest pipe for the fill. Begin from the cross section at the outside edge of the shoulder. Consider only pipes that are available and for which cover is adequate.
For roadway loadings, the maximum culvert diameter is equal to two-thirds of the minimum fill (FT from Figure 6-51). The cover required for culvert protection is equal to one-half the diameter of the culvert or 12 inches (whichever is greater).
For runways and taxiways sustaining aircraft wheel loads, refer to Table 6-12, for the wheel loads and Table 6-13, or Table 6-14, for the minimum cover required.
Step 5. Determine the culvert capacity,  p, and outlet velocity. Use values based on culvert material and slope and Table 6-17.
p, and outlet velocity. Use values based on culvert material and slope and Table 6-17.
Step 6. Determine the number of culvert pipes required. Divide the area runoff,  , by the pipe capacity,
, by the pipe capacity,  p. Round up to the next whole number.
p. Round up to the next whole number.
Step 7. Determine the order length (OL). The OL is calculated by multiplying the number of pipes (NP) times the LIP times a waste factor of 1.15, (See step 3 for the LIP and step 6 for the NP.)
Step 8. Determine the maximum permissible discharge velocity, Vmax. Use Table 6-6, to calculate Vmax for the channel lining into which the culvert outlet will discharge. Determine the correct pipe to be used. Apply the following criteria in your calculations:
- Be sure the outlet velocity is equal to or less than the maximum velocity of the channel lining into which the culvert outlet will discharge. If outlet velocity exceeds the soils the outlet must be protected against erosion.
- Use the least number of culvert pipes possible to carry the total flow and still be consistent with the above criteria.
Example (Unsubmerged Inlet):
Determine the most economical pipe size and the quantity of pipe required for a culvert located under a runway, with the general data cross section given below. The maximum using aircraft weight class for this example will be an SR-71C.
No headwall will be constructed down-stream. The following are known conditions:
- Aircraft SR-71C. (Refer to Tables 6-12 and 6-13.)
- Culvert weight type = 9.
 to be handled by culvert = 32 cfs.
to be handled by culvert = 32 cfs. - Soil type is bare SC; therefore, the maximum allowable outlet velocity = 3-4 fps.
- Pipe sizes available: 24-, 30-, 36-, and 42-inch CMP, 10 gage.
Referring to Figure 6-52, note that the following information is required before design can be accomplished:
- Horizontal length of one culvert, L.
- Slope of culvert pipe needed to determine the flow characteristics of various pipe diameters (see Table 6-17) and which is a portion of the critical fill depth, Ft.
- Critical fill depth, Ft, in order to determine if the cover over the pipe meets the requirements of Table 6-13.
Solution:
Step 1. Determine the runoff rate. Given for this example,  = 32 cfs.
= 32 cfs.
Step 2. Determine airfield culvert use.
Step 3. Calculate the critical dimensions. Computations should be made in the following sequence (see Figures 6-52 and 6-53):
- Determine the difference in elevation between the edge of the runway and the culvert upstream invert.
F1 = EL1 - EL2
F1 = 607.00 - 600.80 = 6.20 ft
- Determine the horizontal distance between the culvert invert and the shoulder edge.
S1 = F1 x X
S1 = 6.20 x 10 = 62 ft
- Determine the difference in elevation between the edge of the runway and the culvert outlet and fill slope.
F2 = EL3 - EL4
F2 = 607.00 - 599.62 = 7.38 ft
- Determine the actual slope of the culvert.
- Determine the incremental elevation difference between the elevation of the upstream invert and the invert of the culvert at the critical fill section.
0.005 ft/ft = 0.5 percent
F3 = S x S1
F3 = 62 X 0.005 = 0.31 ft
- Determine the depth of critical fill section.
Ft = F1 + F3
Ft = 6.2 + 0.31 = 6.51 ft (Length of horizontal projection of the culvert.) The upstream invert elevation to downstream invert elevation is--
LIP = S1 + TW + S2 + 2 ft
LIP = 62 + 100 + 73.8 + 2 = 237.8 ft: (Round Up to 238 ft)
NOTE: These computations depict the cross section and Figure 6-53, summarizes the calculations.
From these calculations, it has been determined that--
- The actual length of the culvert is 235.8 feet, rounded up to an even value of 236 feet. A 2-foot projection is added because there is to be no downstream headwall. This gives a culvert length of 238 feet for a single pipe.
- The slope of the culvert is 0.005 foot per foot or 0.5 percent.
- The depth of fill at the critical section is 6.5 feet (rounded to the nearest tenth of a foot).
Step 4. Determine the largest pipe for the fill. Prepare a table as shown in Table 6-18 and fill in all known values. Start by entering the largest pipe available, Dp, into the table. Subtract Dp from total fill, FT, to get fill critical, FC. represents the actual cover over the pipe at the critical section. Compare FC to cover required, CR.
To find CR for aircraft, refer to Table 6-12, which indicate that an SR-71C aircraft has a culvert weight type (WT) of 9. The CMP available is 10 gage. With this information, refer to Table 6-13, and select chart 9, corresponding to culvert WT 9. The diameters and cover are given in chart 9 under the 10-gage line. Starting with the largest pipe available, 42-inch or 3.5 feet, is 4.0 feet (interpolated between pipe diameters.) Enter this value in Table 6-18. The 42-inch pipe (3.5 feet) cannot be used because its actual cover is 3.01 feet against a required cover of 4.0 feet. Repeat the process using the next smaller pipe available, 36-inch pipe. It has a of 3.51 feet and a of 3.5 feet. This pipe will work.
Step 5. Determine the culvert capacity. Use Table 6-17, to find the capacity and velocity for the 36-inch pipe.
The slope of the culvert is 0.5 percent. Entering the graph from the top (pipe diameter), move down the column until you intersect with the slope in the left-hand column. This will slate the quantity of flow in the pipe. The velocity of flow is shown by following the respective shaded or unshaded areas down and to the left until it ends in the velocity column, 4 feet per second.
The 36-inch pipe has a capacity of 27.5 cubic feel per second for the 0.5 percent slope. The velocity indicated is 4 feet per second.
Step 6. Determine the number of pipe required to carry the flow by dividing the total ( ) of 32 cubic feet per second (step 1) by the pipe capacity, 27.5 cubic feet per second (step 5) and rounding up to the next whole pipe. For this example, the number of pipe required is 32/27.5 = 1.2 or two 36-inch diameter pipes.
) of 32 cubic feet per second (step 1) by the pipe capacity, 27.5 cubic feet per second (step 5) and rounding up to the next whole pipe. For this example, the number of pipe required is 32/27.5 = 1.2 or two 36-inch diameter pipes.
Step 7. The next step is determining the length of pipe to be ordered. The order length is calculated by multiplying NP (Step 6) times LIP (step 3) times a waste factor (WF). Since pieces of material will be damaged in manufacturing, handling, transporting, and assembling, an additional amount over the actual in-place length will be required. This value has been determined to be 15 percent of the total length of pipe required. For this project, the pipe selected will be 36 inches in diameter with a length in place of 476 feet. The length to order will be--
NP x LIP x WF
2 x 476 x 1.15 = 1,094.8 ft
The pipe comes in 2-foot increments; therefore, the value of 1,094.8 is rounded up to the next even value, or 1,096 feet of pipe.
PONDING AREAS
Ponding is the accumulation of runoff at the inlet of a drainage structure resulting from the inability of the system to discharge more of the runoff than the rated capacity of the structure.
Military drainage structures in the TO are designed to discharge the runoff based on the 2-year design storm which, by definition, is expected to be equaled or exceeded at least once in the design period. Thus, a storm more severe than the design storm may occur and generate excessive runoff, overloading the drainage structures. In anticipation of this event, design the areas around the inlets of drainage structures to accommodate a certain amount of pending.
In some cases, due to limitations in culvert cover and space, terrain conditions, time, materials, or other conditions, a system may not be able to take care of the runoff from the design storm. To provide for this, include sufficient pending areas in the original plan to prevent flooding of vital areas. The pending areas store excess runoff until the intensity of the storm decreases and the structure can handle the flow.
When possible, military drainage systems are designed to pass the runoff from the design storm without pending. However, some provision for pending may be made in those areas where flooding for a period of time will not affect the facility's operational status.
The following specifications are generally adhered to in the design of pending areas for military installations:
- The edge of the pond must be at least 75 feet from the edge of the pavement when used for runway and taxiway design.
- When a pond is used with road fills or embankments, the depth of the pond will be determined by the porosity of the fill, the amount of freeboard required to prevent overtopping of the road, the height of the headwall and wing wall, and the time allowed for the pond to empty. When pending is anticipated, the adjacent fill side slope should be made less steep to prevent the sloughing of saturated fill.
- The pond must be drained before damaging infiltration of the subgrade can occur. The actual time during which pending is allowable will depend upon the type and condition of the soil in the pending area and the embankment. In general, this period will be no more than four hours from the start of the storm.
In designing pending areas, the following assumptions are made to simplify the calculations and to retain satisfactory accuracy:
- A culvert discharges its design capacity before runoff starts to accumulate at the inlet and form a pond.
- An increase in the head because of pending does not increase the discharge capacity of the culvert.
The determination of permissible volume, the preparation of runoff curves, and the soil analysis must be done before designing pending areas to meet the above specifications and assumptions.
PERMISSIBLE VOLUME
The volume of permissible pending is determined by the elevations of the area available for such pending and the surrounding areas. A contour map showing the final grading plan is required to compute the volume of permissible pending. By inspection, a contour line may be selected to provide a pending area located a safe distance or elevation from the pavement. Pending volumes may be computed from the con tour map by the average-end-area method. This method is the average of the areas, in square feet, enclosed by two adjacent contour lines and multiplied by the contour interval in feet.
where--
V = volume in cubic feet
A = area of the first contour in square feet
B = area of the next contour in square feet
b = vertical distance, in feet, between contours (contour interval)
As an example of computing the volume for ponding, consider the contours shown in Figure 6-54. Water can be safely ponded to the 66-foot contour line. The bottom of the inlet end of the culvert is at an elevation of 62 feet. Use a planimeter, or any other method, to determine the total area enclosed by each contour. In this case, the 66-foot contour line encloses 25,000 square feet. The 64-foot contour line encloses 10,000 square feet. It should be noted that the contours are concentric: the 66-foot contour-line area includes the area bounded by the 64-foot contour line.
The total volume of the pending area is--
10,000 + 35,000 = 45,000 cubic feet
A further example of the computation of pending volumes by the average-end-area method is shown in Figure 6-55. Assume that the pending area extends to the 68-foot contour line. Determine the volume of the pond. The 68-foot line encloses a total area of 30,000 square feet.
The total volume available for pending will be 10,000 + 35,000 + 55,000 = 100,000 cubic feet, if the pending area extends to the 68-foot contour line.
RUNOFF CURVES
To determine the amount of water an area will contribute to a pond, a cumulative runoff curve must be plotted. The following example shows how such a curve is prepared:
Example:
An area has 33.3 acres, consisting of 23.3 acres of impervious soil and 10 acres of paved surface. The weighted C value is 0.75, the TOC is 13 minutes, and the location intensity is 2.2 inches per hour for a 1-hour storm with a 2-year frequency.
Prepare a cumulative runoff curve based on the data given. Pending may be required reduce the culvert size.
Tabulation of Data--Rational Method
All data required to plot a cumulative to runoff curve, using the rational method, is shown in Table 6-19. Each column is prepared as follows:
Column 1 is a tabulation of time in minutes. Any similar combination of time increments can be used as long as enough properly spaced points are obtained to plot a smooth curve. The cumulative runoff curve is constructed by plotting time, in minutes (column 1), against volume in cubic feet (column 6).
Column 2 is the product of the runoff coefficient, C (as determined for the area using the rational method), and the area in acres.
Column 3 is the intensity, in inches per hour, for each one of the minute values of column 1. These values are obtained from the standard intensity-duration curve number 2.2 in Figure 6-4. The value of 2.2 is the location intensity, in inches per hour, of the 1-hour, 2-year storm as specified in the given conditions.
Column 4 is the rate of runoff,  , in cfs, for the entire interval of time shown in column 1. It is obtained by multiplying columns 2 and 3 (
, in cfs, for the entire interval of time shown in column 1. It is obtained by multiplying columns 2 and 3 ( = CIA).
= CIA).
Column 5 is the time, in seconds, given in column 1.
Column 6 is the quantity of water supplied to the pond for the time given in column 1. For the first five minutes of rainfall, the quantity of water entering the pond is given by--
Column 6 = (column 4)(column 5)
Column 6 = (163)(300) = 48,900 cubic feet
After 20 minutes from the start of rainfall, the volume of water would be equal to 105 x 1,200 or 126,000 cubic feet, if no water was released from the pond.
Preparation of Cumulative Runoff Curve
The cumulative runoff curve is obtained by plotting the volume (column 6, Table 6-19) obtained by the rational method, on the vertical axis and the time, in minutes (column 1, Table 6-19), on the horizontal axis. The cumulative runoff curve for the data listed in Table 6-19 is shown in Figure 6-56.
Analysis of Cumulative Runoff Curve
Based upon the data given in the problem, the flow for the culvert design shown in Figure 6-55 would be determined as follows:
 = CIA
= CIA
where--
C = 0.75
I = 4.9 for a TOC of 13 minutes and a location intensity of 2,2 inches per hour for the 1-hour, 2-year storm
A = 33.3 acres
 = 0.75 x 4.9 x 33.3 = 122.4 cfs. The number of culverts at a slope of 1.2 percent (Figure 6-55) when
= 0.75 x 4.9 x 33.3 = 122.4 cfs. The number of culverts at a slope of 1.2 percent (Figure 6-55) when  = 122.4 would be as follows:
= 122.4 would be as follows:
30-inch pipe at 24 cfs = 6 pipes
36-inch pipe at 38 cfs = 4 pipes
42-inch pipe at 57 cfs = 3 pipes
48-inch pipe at 80 cfs = 2 pipes
60-inch pipe at 140 cfs = 1 pipes
These pipes in the above sizes and quantities will pass the flow without pending.
ANALYSIS FOR PONDING
The safe volume for pending is 100,000 cubic feet. The requirement is to reduce the flow past the outlet point by using a single culvert and allowing pending at the inlet.
Table 6-17, reveals that a 30-inch CMP culvert (n = 0.024) on a 1.2-percent slope discharges 24 cfs. Assuming that the pipe always discharges at the rated capacity, the cumulative discharge is a straight-line function for any time interval with a line passing through the origin.
Continue these straight lines so that they intersect thew cumulative runoff curve. At the point of intersection, the cumulative runoff will have equaled the cumulative amount of water passed by the culvert. From then on, there will be no pending.
Knowing how long the pond will exist behind the inlet, next determine whether or not the pending area is large enough. Figure 6-56 shows that the greatest vertical distance between the cumulative runoff curve and the 30-inch cumulative discharge volume is line P. Line P represents the maximum volume of water ponded behind the 30-inch culvert.
Measuring line P by the vertical scale used in Figure 6-56 indicates that the maximum pending volume will be 115,000 cubic feet. At 42 minutes the cumulative supply curve shows that 175,000 cubic feet of water have been supplied to the pond by the rain storm. At the end of 42 minutes, the 30-inch culvert has theoretically been able to discharge 60,000 cubic feet. Therefore, the difference between the quantity supplied (175,000 cubic feet) and the quantity discharged (60,000 cubic feet) is 115,000 cubic feet, which must still be in the pond.
In view of the fact that the safe pending volume is only 100,000 cubic feet, 30-inch CMP is unsatisfactory because the safe pending volume would be exceeded.
Make the same calculations for 36-inch culvert. In this case, the pond volume will be 75,000 cubic feet with a pond time of 95 minutes. Since the safe pending volume of 100,000 cubic feet and the 4-hour limit on the pending time are not exceeded the 36-inch culvert is satisfactory. In addition, the excess volume of 25,000 cubic feet will be available for storms that may exceed the design storm.
ADVANTAGES OF PONDING
Although pending is an added safeguard against the effects of storms more severe than the design storm, its primary use is as an economy measure. Pending allows for reductions in the size of culvert pipe necessary to handle runoff. However, if additional pipe or other construction is required for pending, check the additional cost against the savings in reduction of pipe size. Ponding appreciably reduces pipe sizes for areas that have a short TOC. For longer TOCs, pending has little or no effect on pipe sizes. The use of pending as an economy measure is often restricted by the area available for pending. This area should be sufficient to satisfy the requirements of the design storm. It should also have enough reserve capacity to take care of storms more intense than the design storm. Facilities for pending should be coupled with initial grading operations, if possible, to secure the most efficient use of personnel and equipment.
DROP INLETS AND GRATINGS
Drop inlets, vertical entrances to a culvert or a storm drain, may be used to lower the elevation of the culvert inlet below ditch elevation. This is done where fill does not provide sufficient cover or where discharge velocity is erosive and can be controlled only by changing the slope. For storm drains (underground culverts or conduits designed to carry surface runoff), drop inlets are used to collect surface runoff from paved and turfed areas, street gutters, and ditches. A typical drop inlet is shown in Figure 6-57.
A framework of bars, or a perforated plate called a grating, passes the storm runoff into a drop inlet. The grating serves as both a filter and a cover for the inlet. Gratings are shown in Figure 6-58.
CONSTRUCTION OF DROP INLETS AND GRATINGS
Drop inlets should always be protected with some type of grating. An expedient grating can easily be fabricated using reinforcement bars welded together. These gratings should be spaced to readily admit debris which will pass unobstructed through the culvert. A drop inlet may be constructed of concrete, brick, timber, or CMP sections.
Inlet grating should be fabricated of steel bars, steel plate, cast iron, or reinforced concrete with adequate strength to withstand the anticipated load. The loads may range from the weight of debris collected over the grating to vehicle or aircraft wheel loads.
Inlet grating should be placed 0.2 foot below the grade. This will allow for the settlement of the area around the grating and will provide a sumped area to ensure complete drainage around the grating and positive interception of surface and gutter runoff.
To determine the proper size of grating--
1. Determine the peak rate of runoff,  , from the area that drains into the drop inlet. This will be the required discharge capacity,
, from the area that drains into the drop inlet. This will be the required discharge capacity,  , of the grating.
, of the grating.
2. Determine the load (depth of water or head) on the grating at times of peak runoff. When a drop inlet is used in a ditch, gutter, or pending area, the head will be the depth of water running in the ditch or gutter, or the depth of the pond.
3. Knowing the head, H, and the design discharge capacity,  , refer to Table 6-20, to select the minimum size grating required.
, refer to Table 6-20, to select the minimum size grating required.
4. Multiply the required grating size by the appropriate safety factor to determine the actual grating size to use.
A safety factor of 50 percent (1.5 x total grating area) for paved areas and 100 percent (2 x total grating area) for turfed areas should be added to the grating-area measurement to compensate for debris caught in the openings.
Grating openings should be at least 18 inches long and should be placed parallel to the direction of flow.
The area of the grating openings is estimated at 50 percent of the total grating area. When using bars with large openings, determine the area of grating openings.
MAINTENANCE OF DROP INLETS AND GRATINGS
Drop inlets and gratings require continuous maintenance because debris collects at the openings. A maintenance schedule must be established to check and clean debris from the inlets and gratings. If these openings are not kept clean, a pond could form at the inlet, resulting in damage to nearby structures. This damage could consist of saturation of the subgrade by the pond or direct flooding of adjacent areas. Periodic maintenance of drop inlets should include removing the cover and inspecting and cleaning the chamber.
Expedient drop inlets of the type shown in Figure 6-39, view (A), must be covered with bars. If the box is left open, it will tend to fill with debris making cleaning difficult, especially if a pond has developed.
SUBSURFACE DRAINAGE
SUBSURFACE DRAINAGE CRITERIA
When surface failures prove that natural subsurface drainage is inadequate, it becomes necessary to determine if a subsurface drainage system is needed, and if so, what type to install. Generally, subsurface drainage may be divided into three classes: base drainage subgrade drainage, and intercepting drainage.
Base drainage generally consists of subsurface drainpipes laid parallel and adjacent to pavement edges with pervious material joining the base and the drain. Figure 6-59 shows a typical section of base drainage.
Base drainage is required where frost action occurs in the subgrade beneath the pavement and where ground water rises to the bottom of the base course through natural conditions or from ponding of surface runoff. Where pavement becomes temporarily inundated and there is little possibility that the water will drain from the base into the subgrade base drainage will be required. Table 6-21, establishes the criteria to follow in these cases.
Base drainage is also required at the low point of longitudinal grades in excess of 2 percent where the subgrade coefficient of permeability is less than 1 x 10-3 fpm. The coefficient of permeability, a property of each soil type, is defined as the discharge velocity at a unit hydraulic gradient. Determine the coefficient of permeability experimentally, either by laboratory test or by an actual field test of the soil involved. The coefficient is expressed in units of velocity such as fpm or centimeters per second (cm/sec). Base drainage is required if the subgrade coefficient of permeability is smaller than the coefficient of permeability indicated in Table 6-22.
Subgrade drainage is required for permanent construction when seasonal fluctuations of groundwaler may be expected to rise to less than 1 foot below the bottom of the course. Figure 6-60, shows a typical example of a subgrade drainage section. Figure 6-61, will serve as a guide for spacing drains. These drains, although similar to base drains, have a larger area of filter material in contact with the subgrade.
Intercepting drainage is required when water seeping into a pervious layer will raise the groundwater locally to a depth of less than 1 foot below the bottom of the base course. This condition is often encountered in thin, pervious soil layers; in exposed rock cuts; or in seepage from springs. A typical intercepting drainage section is shown in Figure 6-62.
SUBSURFACE DRAINAGE TECHNIQUES
Subsurface water can be controlled through a combination of techniques. The techniques and combinations depend on the conditions existing in the area to be drained. The techniques that follow should be considered when planning and designing subsurface drainage.
Depth of Base Course
The base course may be built up to a specified depth above the groundwater table. Generally, the finished grade must be at least 5 feet above the mean groundwater table level. This technique is feasible when--
- A gravity drainage system is impractical.
- The condition to be controlled is limited to a small area such as a narrow swamp crossing.
- Adequate base-course material is available.
Deep Ditch
Where ditches will not interfere with operations or become a hazard to traffic, deep V ditches with free outfall may be feasible. Easily built and readily enlarged, these ditches provide positive interception and drainage of subsurface water before it reaches the area to be protected. Erosion, maintenance, traffic, and right-of-way are factors to be considered before using this solution.
Natural Drainage Channels
Where possible and practical, water in existing natural drainage channels should be lowered when corresponding effective lowering of the groundwater table will occur. This technique may be particularly effective in pervious soil.
Blind Drains
Blind or French drains are constructed by filling a ditch or trench with broken or crushed rock. The top surface of the rock may be left exposed so that the trench will act as a combination surface and subsurface drain, or the rock may be covered by a relatively impervious soil so that no surface water can penetrate. The latter is the general practice. In general, French drains are not recommended for permanent construction because they tend to silt up over time. In TO construction, these drains are often used as a substitute for perforated or open-joint pipe or on filter materials used with such piping.
Subsurface Pipe
In cases where a V-type or other open-ditch type drainage system is not practical, it may be necessary to resort to construction of subsurface drainage. Failure of the subsurface system stemming from improper control of the grade, the bedding, the pipe placement, the placement of filter material, or other installation work gives no warning prior to failure. Such failure is extremely difficult to repair when discovered.
The most common form of subsurface drainage is perforated pipe. Where the perforations do not extend completely around the circumference of the pipe, the pipe is generally laid with the holes down and the joints closed. Materials used in manufacturing this type of pipe are corrugated metal, cast iron, vitrified clay, nonreinforced concrete, bituminized fiber, and asbestos cement.
Bell and spigot pipes can be laid with open joints. If the filter material has been properly designed, collars are not needed over the joints. This type of pipe is generally made of vitrified clay, nonreinforced concrete, or cast iron.
Porous concrete pipe is laid with closed joints. It collects water by seepage through the wall of the pipe and should not be used where sulfated waters may cause disintegration of the concrete.
Farm tile is laid with butt joints slightly separated to permit collection of water through the joint. Because of its low resistance to high-impact loads, farm tile is not recommended for use on airfields.
Materials commonly used in manufacturing farm tile are clay or concrete.
Combination Drainage System
Combination drains, which attempt to handle both surface runoff and subsurface water in the same pipe system, are recommended. Surface runoff often carries sediment and soil from the drained area into the system. This clogs the system and causes flow stoppage. For this reason, subsurface drainage systems using some form of piping are generally sealed so that surface runoff cannot enter. The only drainage system which will satisfactorily handle both surface runoff and subsurface water is the open channel or ditch.
PIPE-LAYING CRITERIA
There are essentially four different types of pipe available for subsurface drainage, as previously mentioned. They should be laid according to the following specifications:
- The minimum slope for subdrainage pipe is a 0.15-foot drop in elevation per 100 feet of length. The elevation of a pipe at any particular location is generally specified by the invert elevation, in which the invert is defined as the lowest point in the internal cross section of the pipe at the particular location.
- Manholes should be provided at intervals of not more than 1,000 feet, with flushing risers between manholes and at dead ends as shown in Figure 6-60.
- Pipe should be at least 6 inches in diameter with 6-inch pipe being used for all drains. With long intercepting lines or extremely severe groundwater conditions, 8-inch or larger pipe may be necessary.
- The center of subgrade drains should be located at least 1 foot below the bottom of the base course and not less than 1 foot below the groundwater table. Normally, subgrade drains are required only at the edges of pavement areas where the soil is pervious and drains well. However, local groundwater conditions and base and subgrade soil characteristics may require closer spacing of the drains. When the drain discharges into a culvert or any considerably larger pipe, it should discharge above the water level in the larger pipe. When the drain discharges into a pipe of equal or only slightly larger size, it is generally better 10 bring the drain in above the receiving drain and make a vertical connection between the two. This will prevent the water from backing up in the drainage pipe since these pipes rarely flow full.
- When the impervious layer is at a reasonable depth, intercepting drains should be placed in the impervious layer below the intercepted seepage stratum. The quantity of water collected by an intercepting drain is difficult to determine, but in general, 6-inch pipe is sufficient for lengths up 1,000 feet.
VERTICAL WELLS
Vertical wells are sometimes constructed allow trapped subsurface water to pass through an impervious soil or rock layer to a lower, freely draining soil layer. If drainage is obstructed, additional wells are built or the pocket is drained with an easily maintained lateral subdrain system. Vertical wells S are often used in northern latitudes where deep freezing is common. They permit fast runoff from melting snow to get through the frozen soil and reach a pervious stratum. Under such conditions, the bottoms of these wells are treated with calcium chloride or a layer of hay to prevent freezing.
FILTER MATERIAL
A layer of filter material approximately 6 inches deep should be placed around all subsurface piping systems. The selection of the proper filter material is very important since it determines, to a great extent, the success or failure of the drainage system. The improper selection of filter material can cause the drainage system to become inoperative in one of three ways:
- The pipe may become clogged through infiltration of small soil particles.
- Particles in the protected soil may move into or through the filters, causing instability of the surface.
- Free groundwater may not be able to reach the pipe.
Criteria have been developed, based upon the mechanical-analysis soil curve, to prevent the above failures.
A great deal can be learned about gradation characteristics of a particular soil by observing the soil curves on the mechanical analysis chart. Well-graded soils generally have a smooth, grain-size curve with gradual changes of slope. Poorly-graded, uniform soils generally have a very steep grain-size curve. Skip-graded soils have a grain-size curve with a characteristic hump in it. The filter material in skip-graded soil tends to segregate during placement. The grain-size curves in Figure 6-63 show various gradation characteristics.
A coefficient of uniformity, value of less than 20 is desirable to prevent segregation of coarse and fine-grain particles, especially during placement. For the same reason, skip-graded material should not be used. Placing the filter material while it is wet can reduce segregation.
Filter material can clog a pipe by moving through the perforations or openings.
Prevent this by using the following specifications:
Use the following methods to prevent particles from the protected soil from moving into or through the filter or filters:
To permit free water to reach the pipe, the filter material must be many times more pervious than the protected soil. This condition is fulfilled when--
If it is not possible to secure a mechanical analysis of available filter materials and protected soil, concrete sand with mechanical-analysis limits as shown in Figure 6-63 may be used. Experience has indicated that a well-graded concrete sand is satisfactory as a filter material in most sandy, silty soils.
STEPS IN FILTER DESIGN
Obtain a mechanical analysis of each sandy soil from several readily available sources. Obtain a mechanical analysis of the subgrade soil (protected soil) at the bottom of the trench which will be in contact with the filter material.
Plot the mechanical analysis of each soil on semilogarithm paper and draw a curve for each soil.
From the mechanical-analysis curve for each soil, determine the diameter, in millimeters (mm), of the particle of each sample. Ten percent of these particles are finer (by weight), D10. The subscript "10" indicates the percentage, by weight, of the soil sample which is finer (smaller in diameter) than the particle in size D10. Similarly, determine the D15, D50, D60, and D85 particle size for each soil.
Determine the slot width or hole diameter, in millimeters, of the type of pipe to be used.
Check the coefficient of uniformity, CU, to ensure--
Check the design criteria for clogging of pipe openings to ensure--
Check the design criteria for movement of particles from the protected soil (subgrade) through the filter material to ensure--
Check the design criteria for relative perviousness to ensure--
Select that filter material which best meets the above criteria.
Install pipe to grade, bedded and surrounded with the selected filter material as shown in Figure 6-58, 6-59, or 6-60, respectively.
SELECTING FILTER MATERIALS
Filter material should be selected with a view toward the simplest construction and the lowest cost. To further this end, try to use only one layer. If several layers of filter material are required, one layer should be confined to the region around the pipe openings and another layer placed between it and the protected soil, as shown in Figure 6-59. In this case, the designer selects a filter material for use around the pipe according to the filter design formulas. The second filter material is then designed to protect both the inner filter material and the surrounding soils. In other words, the design of a multilayer filter for a subdrain system should proceed outward from the inside filter material to the subgrade soil being protected.
Example (Selecting Filter Material):
A suitable filter material must be selected for a 6-inch pipe with ¼-inch diameter perforations to protect a subgrade soil with an E curve (shown in Figure 6-63). The soils represented by curves A and B are readily available from local borrow pits.
Tabulate data from the mechanical-analysis curves.
Check the coefficient of uniformity of both soils.
Thus, both soils A and B satisfy the requirement that the coefficient of uniformity be less than 20.
Apply design criteria to soil A.
Soil A is unsuitable because movement of the subgrade soil through the filter material is possible.
Apply design criteria to soil B.
Note that the soil particle size is usually given in millimeters, while the hole size is usually given in inches. The two dimensions must be expressed in compatible units before the preceding formula is used. To make this conversion, multiply the size of the pipe perforations, in inches, by 25.4 which represents the number of millimeters per inch. For example, with soil B under discussion--
which is > 1.0.
Thus, soil B satisfies all the criteria for a good filter material while soil A does not.
INSTALLATION OF A SUBDRAINAGE SYSTEM
The most efficient and most practical type of subdrainage system is one which adequately performs the operations for which it was intended and, in addition, was installed with the care and skill consistent with its purpose. Any attempt to lower the quality of construction or to use a sketchy or inadequate subdrainage system can result in disastrous failures. Conversely, any attempt to install an elaborate system of underground piping where a simple V ditch would serve as well is inadvisable.
SECTION IV. SURFACE DRAINAGE DESIGN IN ARCTIC AND SUBARCTIC REGIONS
APPLICABILITY
This section discusses the problems involved in the design of drainage facilities in arctic and subarctic regions. While the design data presented has been developed primarily for Alaska, the methods used are generally applicable to other arctic and subarctic regions.
Arctic
Arctic is defined as the northern region which the mean temperature for the warmest month is 50º Fahrenheit (F) or less, and the mean annual temperature in is below 32º F. In general, the arctic coincides with the tundra region north of the limits of trees.
Subarctic
Subarctic is defined as the region adjacent to the arctic where the mean temperature is 32° F or below for the coldest month and 50° F or above for the warmest month, and where less than four months have a mean temperature above 50º F. In general, the subarctic coincides with the circumpolar belt of dominant coniferous forests.
HYDRAULIC CRITERIA FOR COLD CLIMATES
Rainfall
A study of rainfall intensity-frequency data recorded at arctic stations indicates a considerable variance between the average intensity of rainfall for a period of one hour and the average precipitation rates of comparable frequency for a duration of less than one hour. This is evidenced when compared with similar rainfall in the continental United States (CONUS). Even within the area of Alaska, there was a noticeable difference between the rains at Juneau and those at Fairbanks. The higher values for rainfall intensity were used to develop design intensity-duration (supply) curves, which are shown in Figure 6-64. For design purposes, a minimum rainfall rate of 0.2 in/hr is recommended, even where maps of intensity-frequency Design-storm index. One-hour rainfall intensities having various average frequencies of occurrence in the arctic and subarctic regions of Alaska are shown on maps in Figure 6-65. This figure, on which rainfall depth curves are superimposed, is known as a design-storm index. The curves are labeled by the one-hour amounts of rainfall that are represented; these, in turn, are coordinated with the intensity-duration or supply curves of Figure 6-12, Figures 6-64 and 6-65, used in combination, provide a means whereby rainfall intensities sufficiently accurate for runoff computations for any duration may readily be determined.
Elevaton and physiographic orientation. Present information is insufficient to establish quantitative conclusions of the effects of elevation and physiographic orientation for all locations. At the time a site is under investigation, it would be helpful to obtain even a short record of rainfall there. Such a record may be compared with the concurrent portion of a nearby long record and proper frequency values assigned to events in the short record. For example, a temporary gage might have a maximum hourly value of 0.60 inch some summer, and the same storm might produce the summer's maximum hourly value of 0.40 at a nearby long-record station. Similar comparison of other storms for the brief parallel record might confirm the ratio of 6 to 4 as an expression of the difference in the orientation, exposure, and elevation of the two stations. This ratio could then be applied to the known 2-year, 1-hour value of the long-record station to get the estimated 2-year, 1-hour value for the short-record station. If the long-record station has a 2-year, 1-hour value for the construction site, it would be 6/4 of 0.5 or 0.75. Arrangements usually can be made for borrowing a rain gauge for temporary use from the meteorological agency of the area in which the project is to be located.
Infiltration
In permafrost areas, infiltration for design purposes should be considered zero. In other areas, a good guide may be obtained when test borings are made. Values normally would not exceed about 0.5 inch per hour for coarse sands and gravels and would be as low as 0.1 inch per hour for clayey soils with low permeability.
STORM-DRAIN DESIGN
The type and capacity of storm-drain facilities required are determined primarily by the promptness with which design-storm runoff must be removed in order to avoid serious interruption or hazard in the use of important operational areas as well as prevent serious damage to pavement subgrades. It is presumed that all phases of site reconnaissance have been carefully completed and that information is available which shows topography, natural drainage patterns, groundwater conditions, and seasonal frost and permafrost levels.
Basic Considerations
Even though rainfall magnitudes are small in arctic and subarctic regions, drainage is an important factor in selecting an airfield site and planning the construction. The planner should be aware of several features related to drainage in order to ensure a successful design. These features include the following:
- Sites should be selected in areas where cuts or the placement of base-course fills will not intercept or block obvious existing natural drainage ways.
- Areas with fine-textured, frost-susceptible soils should be avoided, if possible. In arctic and subarctic regions, most soils are of single-grain structure with a very small percentage of clay. As a consequence, cohesive forces between grain particles are very small and the material erodes easily. Frozen, fine-textured soil profiles may also contain large amounts of ice lenses and wedges.
- If the upper surface of the permafrost layer is deep and if provisions are made for lower temperatures, design features of a drainage system may be similar to those used in frost regions of the United States.
- The flow of water in a drainage channel has an accelerating effect on the thawing of frozen ground. This may cause the surface of the permafrost to dip considerably beneath streams or channels which convey water. Bank sloughing and significant changes in channel grades become prominent. Sloughing is often manifested by wide cracks paralleling the ditches. For this reason, drainage ditches should be located as far as practicable from runway and road shoulders.
- In many subarctic regions, freeing drainage channels of drifted snow becomes a significant task before breakup each spring. In these areas, it is advantageous to have ditch shapes and slopes sufficiently wide and flat to accommodate heavy snow-moving equipment. In other locations where flow continues year round, narrow, deep ditches are preferable to avoid icings.
- Large, cut sections should be avoided in planning the drainage layout. Thawed zones or water-bearing strata may be en countered and later cause serious icings. Vegetative cover in permafrost areas should be preserved to the maximum degree practicable. Where disturbed, it should be restored as soon as construction permits.
- Inlets to closed conduits are commonly sealed before freeze-up and opened prior to breakup each spring.
- Fine-grained soils immediately above a receding frost zone are very unstable. Consequently much sliding and caving is to be expected on unprotected ditch side slopes in such soils.
- Locating ditches over areas where permafrost lies on a steep slope should be avoided if possible. Slides may occur because of thawing and consequent wet ting of the soil at the interface between frozen and unfrozen ground.
- Maintenance equipment for drainage facilities should include heavy snow-removing apparatus and a steam boiler with accessories for steam thawing of structures which have become clogged with ice. Pipes for this purpose are often fastened inside the upper portions of culverts prior to their placement.
Grading
Proper grading is a very important factor contributing to the success of a drainage system. The development of grading and drainage plans must be carefully coordinated. In arctic and subarctic regions, it is necessary to eliminate soft, soggy areas.
Temporary Storage
Trunk drains and laterals should have sufficient capacity to accommodate the project design runoff. Do not consider supplementary pending above the drain inlets in airfield drainage designs for the arctics and subarctic. Formulate plans in sufficient detail to avoid flooding even during the time of actual construction.
ICINGS
An icing is an irregular sheet or field of ice with no uniformity as to shape, thickness, or size. All icings are similar with regard to laminated structures, indicating that irrespective of shape, thickness, size, or cause, the actual process of formation is the same. Thin films of water traverse over layers of ice or other material and, when exposed to the cold air, freeze and form the first or an additional layer of ice. As water flow continues, the process is repeated, and an icing with horizontal laminations continues to grow until either the source of water supply is depleted or warmer weather begins.
Types of Icings
For the purpose of analysis, icings may be divided into three groups, depending largely on the nature of the source of water supply For icings formed along rivers or streams and adjacent areas having a source of water above or below the riverbed, the term river icing applies. If the source is from groundwater flow above permafrost, ground icing is the term most commonly used. This term should not be confused with ground ice, which is often encountered in the arctic and subarctic as deposits in fine-grained soils. The term spring icing should be confined to when the source of water is from subpermafrost levels or subpermafrost water under hydrostatic pressure. Spring icings are commonly large and thick. Human activity can disturb the ground regime sufficiently to cause or accelerate the formation of all types of icings.
River icings. Most arctic and subarctic streams carry large loads of sediment which are not fed into the channels in uniform quantities Consequently, the rivers are quite wide and relatively shallow. Many rivers have a braided pattern of several smaller streams within the confines of the main channels. These streams frequently shift in transverse position and often do so during one period of high flow. Winter flow is ordinarily very small and shallow. Freezing penetrates to the bottom of shallow streams quite readily, but the river discharge continues as groundwater flow beneath the riverbed. Because of thermal effects of flowing water, the soil below streambeds is unfrozen to greater depths than soil located elsewhere. Consequently, there is a large space for groundwater storage and flow above the permafrost and below all riverbeds. The head motivating ground water flow is ordinarily quite large and can result in large pressures above sections where the groundwater flow is retarded.
Groundwater-flow retardation is a natural process at many river sections because river beds are not homogeneous in water-carrying capacity. Freezing of the water reduces channel area and capacity in some sections more than in others. The formation of anchor ice on the bottom of the streambed results in fur her constriction of the channel cross-section area. The water then finds avenues of escape to the top of the ice via weak points, cracks, and fissures. Here, exposed to the cold atmosphere, the water quickly freezes in thin sheets. This action is progressive, and icing continues to increase in thickness until the supply of water is exhausted or finds a new outlet, or until the beginning of warmer weather. A bridge may shade the streambed and also prevent the deposition of snow. Freezing then would be more rapid beneath the bridge than at either upstream or downstream locations. Subsequent penetrations of frost would diminish groundwater -flow capacity at the bridge section and induce the formation of an icing above or at the site. These icings can be of various shapes and sizes, depending upon the valley topography, the depth of the snow, the intensity of cold, the water supply, and other factors.
Ground icings. Ground icings may take the form of mounds having considerable thickness but small areas. They may also form as crustations if groundwater flow is induced to the surface at points which are not of great lateral spacing but are of about equal elevation. In addition to a supply of water, there is another requisite to the formation of an icing--an area where the water can be exposed to the cold atmosphere. A pavement kept clear of snow offers an excellent site over which flowing water can spread out into a thin film and then freeze. Icings from groundwater above the permafrost are not likely to occur in the arctic, as the permafrost there is too close to the surface to permit any appreciable storage in the active layer. This occurrence is most severe in the southern zones of the subarctic and on slopes which face south. Groundwater flow may be induced to the surface in various ways. It is not essential that the seasonal frost reach the permafrost, although this very effectively blocks groundwater flow. Partial freezing of the active layer reduces the area of the section which ground water must pass. The path of least resistance may lead to the ground surface via a frost crack or fissure or through holes which have previously been made by burrowing animals Water coming to the surface in this way may flow considerable distances down slopes beneath a snow blanket without freezing.
Various met hods have been tried to prevent the occurrence of such icings. Some of these have met with partial success. The frost belt or dam has been advocated by Russian investigators, but this method is effective for only a few years. The thawing in summer is accelerated at the site of the frost dam, and eventually the permafrost degrades sufficiently to permit groundwater flow below the frost dam. Fences and barriers have been used quite effectively under special circumstances.
Spring icings. Icings that occur from artesian, subpermafrost water and springs are ordinarily quilt thick and cover considerable area. Reference is often made to the icing in the Momy River Valley of Siberia. This spring icing is about 15 miles long and 3 miles wide, with an average thickness of about 12 feet. It does not melt and form each year. Spring icings can be controlled quite readily. The temperature of the water emerging from the ground is ordinarily quite high and the water does not freeze quickly if confined to a conduit. In some cases, an insulated conduit may be required to convey the spring water to locations where the formation of icing will do no damage.
Measures Against Icings
River icings. In the case of river icings, depths to permafrost are ordinarily too large to be blocked effectively by accelerated freezing such as is induced by the frost dam or belt. In addition, the subbed river flow is often in excess of what can be stored as ice above the location of the bridge to be protected. The control of river icings then must be concerned with an insulation of streambeds at the critical section.
Ground icings. Ground icings can be controlled to some extent by inducing the ice to form upstream from the site in question. This can be accomplished by the installation of frost belts. In open terrain, some success can be achieved by merely keeping snow removed from a strip crossing the affected area in a direction transverse to groundwater flow. Groundwater flow will be blocked by freezing and forced to the surface upstream from the cleared area. The snow-free area also provides a cold space on which surface flow can spread out and freeze. If necessary, the depth of stored ice can be increased by erecting some barrier to the flow, such as an ordinary wooden-stave snow fence on top of the ice initially formed at the site of the frost belt. Because the process employs the removal of snow, it is essential to shift the position of the belt from year to year in order not to unduly influence the depth to permafrost. In timbered regions, it is obviously necessary to maintain the frost belt at one location to save the expense of tree removal.
Spring icings. If the source of water forming the icing is a spring, then it is necessary to resort to drainage or diversion to control the occurrence. This sometimes requires insulated channels. In the case of springs, flows are ordinarily too large to permit a storage of icc at or upstream from the site.
FORDS, DIPS, CAUSEWAYS, AND BRIDGES
FORDS
A ford is a shallow place in a waterway where the bottom, either naturally or by human improvement, permits the passage of personnel and vehicles. A ford is used instead of a bridge when time limitations, the lack of structural materials, the tactical situation, and the terrain configuration make its use necessary and practical.
An increase in water depth can close a ford for a considerable time. Streams in mountainous and desert country are subject to sudden changes in depth. The increase in depth can be so sudden as to endanger personnel or vehicles in the ford.
Stream bottoms can be of such material that much effort is required to make fords usable.
Reconnaissance
Route reconnaissance should include the selection of possible ford sites. Special emphasis is placed on the requirements to be discussed in this section. Ford reconnaissance and required reports are covered in FM 5-36.
Requirements
The characteristics of a good ford are a slow current (usually less than 2 miles per hour); low, sloping banks; good approaches; and a uniformly increasing bottom depth with a firm bottom material. Requirements of width depth, and bank slopes for fords are given in Table 6-23.
Location. A desirable location for a ford is in the reach of the stream between bends. At this location, the bottom depth is constant between the banks with only a slight channel in the center. The influence of river action on possible fording locations is shown in Figure 6-66. Because of the increased velocity of the water, bends result in a deep channel that is difficult to improve. In the reach, the center channel is not so deep or sharp and therefore is readily adaptable for improvement. In addition, the variation in the shape of the banks is not as pronounced in the reach area as it is at the bend.
Bottom Material. For a natural ford, the bottom material should be hard, durable, and interlocking. Such material will resist cutting by wheeled traffic and erosion. The general terrain will determine the bottom condition, as follows:
- In mountainous country, sudden freshet floods can transport large boulders and stones along the bottom. This material is deposited at the passing of high water or at locations where the widening of the stream reduces the velocity. It may be necessary to remove this material before traffic can cross the ford.
- In terrain of moderate or gentle slopes, the velocity will tend to prevent deposition of fine material. This tendency and the scouring action of the water will leave a good, firm bottom. The bottom material may be disturbed by traffic and will require protection.
- In slightly sloping or flat terrain, streams meander and have low velocity. In addition, there is sometimes a high water table. In such cases, the bottom material may be very soft. Such material will require a completely improved ford with special emphasis on bottom requirements. Timber, lumber, matting, gravel, or gabions can be used to improve trafficabilty.
High-Water Determination. Table 6-23 indicates that a maximum water depth of 2 feet is allowable for truck traffic. To ensure maximum use of the ford, it is necessary to determine the depth at which the stream will flow at frequently recurring times. Estimates of various depths of flow, as shown in Figure 6-67, can be made by direct stream observation, as follows:
Base Flow. Base flow is the normal flow that occurs in a stream when there has been no recent rain. The depth of this flow is dependent upon the quantity of ground water.
High-Water Flow. During the year, many rainfalls normally occur that cause flows above the base level. The velocity of such flows generates a slight erosion cut, as shown in Figure 6-67. The occurrence of such flows tends to prevent the growth of vegetation. Since these flows can occur with relative frequency during the year, the depth of these flows could control the use of the ford. In the event the depth is greater in places than the fording depth of trucks (see Table 6-23), it may be necessary to fill these gaps with rock or gravel. However, such filling might cause the velocity of flow over the ford to be increased to the point that vehicles would have difficulty using the ford.
Flood Flow. In the absence of records, it is necessary to check stream banks for evidence of floodwater levels. The highest level of flood that occurs within a period of two years is of particular interest. The bend of a stream, especially with a high bank on the outside of the bend, would show an erosion cut that can be used to determine the flood level, as shown in Figure 6-67.
Approaches. Carefully note the height of the bank and the type of soil. This information helps to determine construction requirements.
Stream Velocity. The normal stream velocity at the fording site should not exceed 3 fps. This velocity would, in most cases, occur at low or moderate levels.
Cross Section. Make a cross section of a ford location similar to Figure 6-66, and Figure 6-67. Include full details of bank slopes, bottom slopes, bottom variations, and water depth. In addition, determine the average velocity of the stream from measurements taken at equal intervals across the stream.
Channel Condition. Make a record of the character of the streambed. Include vegetation density and type, whether or not the channel is scoured, and the type of soil. This information will determine the value of Manning's n.
CONSTRUCTION
Two phases of construction are required for fords--the development of the approaches and the preparation of the bottom.
The maximum slopes for ford approaches should be as recommended in Table 6-23. Place material cut from the banks off to the side and not in the stream, where it may form an obstruction. Because traffic will wet the slopes and cause eventual deterioration, provision should be made for protecting the surface.
Ford-bottom preparation will depend upon site conditions. Fill short, deep gaps with rock or gravel, preferably retained by wire mesh. Soft, mud bottoms can be improved by covering the bottom first with willow, brush mattresses, or timbers, and subsequently with metal planking, rock, or coarse gravel. Even a hard and tenacious bottom deteriorates under traffic conditions and requires protective maintenance.
Consider these factors when raising the bottom of the ford:
- The depth upstream from the ford increases in proportion to the amount of rise of the bottom of the ford.
- The velocity of flow over the ford increases at an increased fording depth so that vehicles may be difficult to operate and control.
MARKING
Place marking posts at each end of the ford and at as many intermediate points as may be necessary. Mark a post at each end with an index to indicate depth. Warning notices should be clearly and prominently placed to alert drivers that flooding can occur suddenly and without warning.
MAINTENANCE
Examine fords after each flooding. Repair scour damage upstream and downstream with riprap. Remove boulders and other debris to provide a clear passage for vehicles.
DIPS
Dips are paved fords used for the crossing of dry, wide, and shallow arroyos in semiarid regions subject to flash floods.
Reconnaissance
The preferred location of a dip is in the straight run of an arroyo or wash. Determine the width between the banks and the top elevation of the banks. In addition, check the area above the dip site to determine if pending will occur and to what level.
Determine the type of soil in the banks and bottom for construction requirements. In addition, note the size and type of bottom rock. This type of information gives an indication of the volume and velocity of flash floods which move or carry large material.
Investigate the area, especially the banks, to determine the general flash-flood high watermark. This information on the area of the waterway, along with an approximation of velocity as indicated by the rock or other debris on the bottom, gives some indication of the volume of flow. This information will be necessary if bridging is required.
Construction
The subgrade should be of erosion-resistant material or a rock-compacted base, and it should be set between the cutoff retaining walls. The pavement should be of concrete or compacted macadam. The general construction is shown in Figure 6-68.
Other factors of importance are as follows:
- The site should be in the reach of the stream and well away from any bends. There is more erosion in bends than in straight stretches. If a very severe flood occurred, a structure placed in a bend might be destroyed.
- The structure should be set at right angles to the flow to reduce scour.
- The structure must be set at true dry-streambed level to avoid scour erosion or silting. Under no circumstances should the structure be set above dry-streambed level.
Marking
The marking for dips is the same as for fords.
Maintenance
Dips, like fords, must be examined after each flooding, and scour damage upstream and downstream should be repaired with riprap. Remove boulders and other debris. When macadam is used, it can be anticipated that holes may be scoured in the roadway. Consider stockpiling rock adjacent to the area for immediate maintenance repair.
CAUSEWAYS
When it is essential to keep a roadway open during floods of medium intensity, a raised causeway can be used in place of a ford or dip. This type of structure must be well sited, carefully designed to pass the flow, and strongly built. It must incorporate a sufficient waterway at streambed level to permit the passage of the design volume of flow before the flood level reaches the top of the structure. A typical design is shown in Figure 6-69. The main design features of a causeway follow.
Cross-Sectional Area
A sufficient cross-sectional area must be provided to ensure that the flood level will not submerge the structure. Consider the following basic elements:
- The size and number of culverts or other elements must be sufficient to pass the flow. When the water elevation upstream and downstream is above the culvert crown, pipe equations should be used for flow design.
- The inverts or lowest parts of the culverts must be set at streambed level.
- The cover over the stream must be sufficient to protect the waterway against traffic loads.
Embankment
Protect both the upstream and downstream faces of the embankment against scour and erosion. Heavy flooding or overtopping of the structure will require complete protection in the form of a concrete or rock-gabion facing. To further prevent excessive scour and erosion, carry the protective facings below the streambed and provide them with aprons. Anchor the ends of the structure securely into the banks in such a way that there is minimum obstruction to water flow.
Guardrails
Provide guardrails to guide and direct traffic. Because the structure can be overtopped, be sure to provide for ready replacement of the guardrails.
Maintenance
Inspect the structure for scour or erosion after each flow that causes partial submergence or overtopping. Repair any damage immediately otherwise, at the next heavy flow, the structure could be destroyed. Stockpiling of heavy rock and gabions at each end of a structure may be required.
BRIDGES
This section presents elements of bridge design other than the requirements for structural design Bridges must conform to the requirements of stream hydraulics in the same way as all cross-stream structures such as fords, dips, and causeways.
Location
The location of a bridge should be away from bends in the straight section or reach of the stream (Figure 6-66). In this location, there are moderate, even depths from bank to bank. The deep channel tends to be in the center. Abutments will be placed on the edge of the stream. Because of the even distribution of flow, scour and erosion at the stream pier and bank abutments are not expected to be so excessive as to cause maintenance problems.
Height
The height of a bridge depends upon the flood-flow, high watermark. The height of that mark will determine the profile or superstructure level of the bridges as follows:
- When the flood-flow, high watermark is above the banks, a high-profile or high-level bridge must be constructed to keep the superstructure above the flood level. This type of bridge is well above bank level and may require a considerable length and height of approach.
- When the flood-flow, high watermark is below bank level. a low-profile or low-level bridge can be constructed. This type of bridge presents fewer problems than the high-level bridge, since approach ramps will not have to be constructed.
Abutments
The location of bridge abutments depends upon an analysis of the flood level and the cross section of the stream (Figure 6-70). Analysis proceeds as follows:
Abutments placed at 1A and 1B of Figure 6-70 present the most direct solution because they are located on high, dry ground.
Use of these locations, however, may necessitate more construction effort because of the increased length of the bridge. This increased length could result in the need for intermediate piers and spans. With this method, the full river waterway will be used for the passage of flood water.
Abutments placed at 2A and 2B would reduce construction time because fewer intermediate piers and spans would be required. In addition, the fill in areas 1A-2A and 1B-2B could be accomplished as the bridge is constructed. As can be seen from the figure, this placement reduces the cross section of the waterway. The following techniques could be used to accommodate this reduction in an available cross-sectional area:
- The elevation of the bridge superstructure could be raised to account for the rise in the flood level. In this case, use substantial abutments that are well protected against end scour.
- The superstructure elevation could be left substantially at the original level, and approach ramps over areas 1A-2A and 1B-2B could be constructed as causeways to allow for flow. Care must be taken to ensure that there is no excessive scour or erosion below the culvert outlet that would affect the roadway.
- The roadway approaches in areas 1A-2A and 1B-2B could be depressed below the superstructure level. In this case, the excess flood flow would pass over the roadway approaches, thus relieving the bridge flow. If this action is taken, the roadway may not be usable at all times. Since overflow is anticipated, the construction of these approaches is similar to construction of causeways without the culverts. If the bridge is designed properly, with fording depths as outlined in Table 6-23, it may be usable during floods under extreme conditions.
- When a depressed roadway or an elevated superstructure is used, the approach to the bridge must have a gentle slope to prevent vehicle impact on the abutment and to ensure traffic visibility.
Drainage
The soil behind bridge abutments can become saturated because of rain or other conditions. This saturation can take place whether the approach road is at the natural grade of the soil or it is a filled approach. When saturation occurs, static hydraulic pressure on the back face of the abutment generates additional overturning movement. With wood abutments, this condition is relieved naturally. However, if concrete abutments are used, the pressures can be relieved as follows:
Step 1. Use weep holes to pierce the abutments with bagged gravel backing on soil side.
Step 2. Place gravel backing against the lower part of the abutment drained by a perforated pipe at the footing elevation. Set the pipe to drain out at the sides of the abutment.
EROSION CONTROL
Erosion must be controlled to maintain an effective and clear drainage system with a minimum of maintenance and to reduce hazardous dust conditions. Erosion may occur at any point where the force of moving water exceeds the cohesive strength of the material with which the water is in contact. Proper design of side slopes in cut and fill sections (based on the type of soil) will reduce the need for extensive erosion control measures. However, additional control is usually required. Most methods of control are based on dissipating the energy of water, providing an erosion-resistant surface, or some combination of these techniques. This chapter acquaints the military engineer with the means available to reduce or eliminate the erosive force of water.
NONUSE AREAS AND OPEN CHANNELS
Terracing is a control measure designed to dissipate the energy of overland flow in nonuse areas. Turfing, paving, Gunite lining, and placing riprap are control methods designed to cause turbulence and to increase retardation, thereby dissipating the energy of flow in open channels such as ditches and pipe outfalls. In cases where even riprap will be eroded, the use of gabions is a speedy and relatively inexpensive means of dissipating energy.
TERRACING
A terrace is a low, broad-based earth levee constructed approximately parallel to the contours of the topography. A terrace either intercepts and holds the water until it infiltrates the soil or moves it as overland flow to a suitable discharge point. A hardy, vigorous turf should be planted to hold the disturbed soil in place. Vertical spacing and longitudinal gradients of terraces are given in Figure 6-71.
TURFING
Ditches are often protected by placing strips of sod (held in place by wooden boards or stakes) perpendicular to the flow path at intervals along the ditch, as shown in Figure 6-72.
PAVING AND GUNITE LINING
Ditches having grades in excess of 5 percent usually require paving or a Gunite lining. Where a slope equals or exceeds 5 percent, paving must be extended down slope at least to the point in the ditch at which the erosive energy of the water is controlled or absorbed without erosion damage.
Paving with either asphalt or portland-cement concrete provides superior erosion-resistant linings in gutters, ditches, and outfall structures.
Gunite lining of ditches controls erosion effectively. Gunite is a mixture of portland cement and sand with water added just before the mixture is sprayed from a high-pressure nozzle onto the surface being protected. The Gunite lining is formed over steel mesh placed over the bottom and sides of the ditch. Gunite is sprayed to a thickness of 1 to 1 ½ inches, with the steel mesh located midway in the thickness. Human resources, time, material and equipment expenses usually limit the use of paving or Gunite linings to only the most demanding conditions in TO airfield construction.
PLACING RIPRAP
Riprap protection should be provided adjacent to all hydraulic structures. When placed on erodible surfaces, it prevents scour-al the ends of the structure. This protection is required on the bed and banks for a sufficient distance to establish velocity gradients and turbulence levels at the end of the riprap.
Riprap can also be used for lining the channel banks to prevent lateral erosion and undesirable meandering. Provide an expansion either horizontally or vertically (or both) immediately downstream from hydraulic structures such as drop structures or energy dissipators. The expansion allows the flow to expand and dissipate its excess energy in turbulence rather than directly on the channel bottom and sides. Riprap has been known to fail from--
- Movement of the individual stones from a combination of velocity and turbulence.
- Movement of the natural bed material through the riprap, resulting in slumping of the blanket.
- Undercutting and leveling of the riprap from scour at the end of the blanket.
Consideration must be given to the selection of an adequate size of stone, the use of adequately graded riprap, the provision of a filter blanket, and the proper treatment of the end of the riprap blanket.
Selection of Size
Curves for the selection of stone size required for protection, with Froude numbers and depths of flow in the channel shown, are shown in Figure 6-73.
Two curves are given. One is for riprap subjected to direct flow or adjacent to hydraulic structures such as side inlets, confluences, and energy dissipators, where turbulence levels are high. The other is for riprap on the banks of a straight channel where flows are relatively quiet and parallel to the banks.
With the depth of flow and average velocity in the channel known, the Froude number can be computed from the following equation:
D50 value can be determined from the appropriate curve.
Curves for determining the riprap size required to prevent scour downstream from culvert outlets with scour holes of various depths are shown in Figure 6-74. Make the thickness of the riprap blanket equal to the longest dimension of the maximum size of stone or 1.5 times D50 whichever is greater.
When the use of large rock is desirable but impractical, substituting a grouted reach of smaller rock in areas of high velocities or turbulence may be appropriate. Grouted riprap should be followed by an ungrouted reach.
A well-graded mixture of stone sizes is preferred to a relatively uniform size of riprap. A recommended gradation is shown in Figure 6-75. In certain locations, the available material may dictate the gradation of riprap to be used. The gradation should resemble the recommended mixture as closely as possible. Consider increasing the thickness of the riprap blanket when locality dictates using gradations with a larger percentage of small stone than shown by the recommended plot. If the gradation of the available riprap is such that movement of natural material through the riprap blanket would be likely, place a filter blanket of sand, crushed rock, gravel, or synthetic cloth under the riprap. The usual blanket thickness is 6 inches, although a greater thickness is sometimes necessary.
Design
An ideal riprap design would provide a gradual reduction in riprap size until the downstream end of the blanket blends with the natural bed material. Unless this is done, turbulence caused by the riprap is likely to develop a scour hole at the end of the riprap blanket. However, the extra effort required to provide gradual reduction in riprap size is seldom justified. Double the thickness of the riprap blanket at the downstream end to protect against undercutting and unraveling. An alternative is a rubble blanket of constant thickness and suitable length, dipping below the natural streambed to the estimated depth of bottom scour.
GABIONS
Gabions are large, steel, wire-mesh baskets, usually rectangular and variable in size, designed to solve erosion problems at a low cost. Widely used in Europe, gabions are now accepted in the United States as a valuable and practical construction and maintenance tool. They can be used in place of sheet piling, masonry construction, or cribbing.
Description and Assembly
Gabions are supplied from manufacturers in flat, folded bundles. For ease in handling and shipping, the number of gabions per bundle varies according to the size of the gabions. The box gabion is a rectangular cage or basket formed of woven, hexagonal, galvanized steel, wire mesh with 4- to 8-inch openings and divided by diaphragms into cells. To assemble, remove a single gabion from the bundle and unfold it on a hard, flat surface to straighten unnecessary creases and kinks. Fold the front, back, and end panels to a right angle to form a box, as shown in Figure 6-76. Securely lace the vertical edge and diaphragms with binding wire.
Installation
Before placing the gabions, make the ground surface relatively smooth and even. Place the assembled gabions in position singly or wired together in groups suitable for handling. It is convenient to place the gabions front-to-front and back-to-back to expedite the stone-filling and lid-lacing operation. Lace the basket along the perimeter of all contact surfaces. Where there is more than one course of gabions, the base of the empty gabions placed on top of a completed row must be tightly wired to the latter as shown in Figure 6-77.
When using 3-foot-high gabions, place them empty and lace for approximately 100 linear feet. Anchor the first gabion firmly and apply tension to the other end with a comealong or by other means to achieve the proper alignment. Anchoring can be accomplished by partially filling the first gabion with stone. While the gabions are being stretched, inspect all corners to make sure the lacing is secure and the corners are closed. Keep gabions taut while they are being filled with stone.
Where water, soil, and atmospheric conditions allow, galvanized wire mesh can have a life of 40 years or more. For soils and water showing a pH factor of less than 7 or more than 12, plastic-coated wire must be used to form gabions.
Filling Procedures
The best filling material is one that allows flexibility in the structure and, at the same time, fills the gabion compartments with a minimum of voids and maximum weight. Ideally, the stone should be small, just slightly larger than the size of the mesh (usually 4 to 8 inches). The stone should be clean, hard, durable, and resistant to weathering and frost action.
Fill the gabions to a depth of 1 foot. Then place one connecting wire in each direction and loop around two meshes of the gabion wall, as shown in Figure 6-77. Repeat this operation twice or until the gabion is filled; then fold the top shut and wire it to the ends, sides, and diaphragms.
Pack the stone inside the compartment as tight as practical. To protect the vertical diaphragm during the filling operation, temporarily place rebars and lace them along the upper edges.
Some manual stone adjustment is required during the filling operation to prevent undue voids. Fill the gabion slightly overfull and allow for subsequent settlement; then lace the lid down with binding wire to the tops of all the sides and to the tops of the diaphragm panels. Since it is necessary to stretch the lid to fit the sides exactly, use a short crowbar or special tool designed for this purpose.
The strong interconnection of all units in a gabion structure is an important feature. It is essential that the lacing be done properly. Adjoining gabions are wired together by their vertical edges. Empty gabions, stacked on filled gabions, are wired to the filled gabions at front and back.
Gabions may be filled by almost any type of earth-handling equipment such as a payloader, crane, conveyor, or modified concrete bucket. The use of rounded stone, if it is available, reduces the possibility of damage to the galvanized wire during mechanical filling.
When the depth of the water is too great for the gabions to be filled on site, fill them at a dry location nearby and place them underwater by crane or barge.
Maintenance and Repair
Maintenance and repair are simple procedures; therefore, gabions are inspected at least once a year. Holes can be patched with small panels of mesh, and broken wires can be repaired by using the method shown in Figure 6-78.
Thickness
The thickness of gabions may be calculated by considering the gradient of the channel, the steepness of its slope, the type of material forming the banks and bed, and the curvature of its course. A 12-inch-deep lining is suggested for channels having reasonably straight alignment, side slopes of less than 35 degrees, and a flow velocity of about 10 fps, as shown in Figure 6-79. Use an 18-inch gabion lining for curved channel sections with a side slope of 45 degrees. Use 36-inch stepped-back gabion protection for sharper side slopes. For a steep channel slope, a combination of lining and weirs may be required.
In the case of easily erodible soil, a layer of filter material or permeable membrane of cloth woven of synthetic fibers is required. The gabion should be filled with stone small enough to allow at least two overlapping layers.
In designing a gabion-lined channel, the roughness factor or coefficient (n) in Manning's formula may be assumed to be between 0.025 and 0.030. If the gabions are grouted, the roughness factor can be assumed to be between 0.012 and 0.018.
Gabion-lined channels may be designed using Manning's equation and the procedures for open -channel design.
Uses
Gabions can be used in the following ways:
- Protective and antierosion structures on rivers (for example, revetments, groins, or spurs).
- Other antierosion structures (for example, weirs, drop structures, and check dams).
- Channel linings.
- Seashore protection.
- Low-water bridges or fords.
- Culvert headwall and outlet structures.
- Bridge abutments and wing walls.
It is often necessary to modify the inlet and outlet of a culvert by using transition structures to reduce entrance losses and to inhibit erosion. Therefore, the two most common devices for which gabions are used are headwalls and outlet aprons.
Headwalls or wing walls are designed to protect the slopes of an embankment against scour, to increase culvert efficiency by providing a flush inlet as opposed to projecting one, to prevent disjointing of sectional-pipe culverts by anchoring the inlet and outlet, and to retain the embankment slope. These structures are built in a variety of shapes: straight, L-shaped, flared, and warped. A typical plan using a headwall and an outlet apron with a culvert is shown in Figure 6-79. Straight headwalls are generally used on small, roadside culverts under driveways and in small channels having a low approach velocity. They are also recommended where there is a tendency for lateral erosion to develop at the outlet.
An apron is often required at the outlet of a culvert to reduce the outlet velocity and thereby inhibit scour. Gabions are well adapted for use here because of their roughness, flexibility, and durability. See Figure 6-80.)
Table 6-24 indicates the type of gabion protection required for various ranges of outlet velocities.
CULVERT OUTLETS
Most culverts operate under free outfall conditions (that is, there is no control of tailwater), and the discharge possesses kinetic energy in excess of that occurring naturally in the waterway. This excess kinetic energy must often be dissipated to control damaging erosion. The extent to which protective works are required for energy dissipation depends on the amount of excess kinetic energy and the characteristics of the material in the outlet channel. In general, scour occurs at average velocities in excess of about 1.5 fps in uniform-graded sand and cohesionless silts, 2.5 fps in well-graded sand, 3.0 fps in silty sand, 4.0 fps in clay, and 6.0 fps in gravel. These velocities should be used only as a general guide.
If possible, make a study of local material to determine its erosion tendencies prior to a decision on the degree of protection required. The study should consider three types of outfalls offering three degrees of protection: plain outlets, transitions, and stilling basins. Plain outlets provide no protective works and depend on natural material to resist harmful erosion. Transitions provide little or no dissipation on the works themselves but result in a spreading of the effluent jet to approximate the cross-section flow of the natural channel, thus reducing the concentration of energy prior to releasing the flow to the outlet channel. Stilling basins result in dissipation of energy on the protective works.
PLAIN OUTLETS
If the discharge channel is in rock or a material highly resistant to erosion, special erosion protection is not required. This type of outlet should be used only if the material in the outlet channel can withstand velocities about 1,5 times the velocity in the culvert. At such an outlet, side erosion from eddy action or turbulence is more likely to prove troublesome than bottom scour.
Cantilevered culvert outlets may be used to discharge a free-falling jet onto the bed of the outlet channel. As a result, a plunge pool will be developed. The depth and size of the plunge pool depend on the energy of the falling jet at the tailwater and the erodibility of the bed material.
TRANSITIONS
Outlet headwalls and wing walls serve the dual purpose of retaining the embankment and limiting the outlet transition boundary. Erosion of embankment toes can be traced to eddy attack at the ends of such walls. A flared transition is effective if it is proportioned so that eddies induced by the effluent jet do not continue beyond the end of the wall or overtop a sloped wall.
As a guideline, it is suggested that the product of velocity and flare angle not exceed 150 degrees. For example, if effluent velocity is 5 fps, each wing wall may flare 30 degrees; but if velocity is 15 fps, the flare should not exceed 10 degrees. Unless wing walls can be anchored on a stable foundation, a paved apron between the wing walls is required. Special care must be taken in the structure design to preclude undermining.
A newly excavated channel may be expected to degrade. Proper allowance for this action should be included in establishing the apron elevation and depth of cutoff wall. Warped end walls provide excellent transitions that result in the release of flow in a trapezoidal cross-section which approximates the cross section of the outlet channel. A warped transition is made at the end of the curved section to reduce the possibility of overtopping as a result of super-elevation of the water surface. A paved apron is required with warped end walls. Riprap is usually required at the end of a transition-type outlet.
STILLING BASINS
At culvert outlets where a high concentration of energy or easily eroded materials make excessive erosion likely, a stilling basin or other energy-dissipating device is required. For TO construction, riprap or simple, concrete stilling basins are usually required. There are many types of energy-dissipating devices such as hydraulic-jump basins, roller buckets, flip buckets, impact-energy-dissipating devices, and stilling wells. In unusual cases involving major structures, the use of a special type of device should be considered. Three types of dissipators which may offer a solution are the hydraulic-jump stilling basin, with details developed at the St. Anthony Falls Hydraulic Laboratory; the impact-energy dissipator, with details developed at the hydraulic laboratory of the Bureau of Reclamation; and stilling wells. These dissipators are beyond the scope of TO construction. Design procedures are not included in this manual.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|