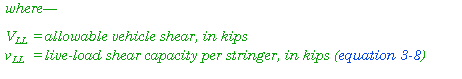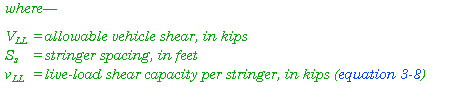Part Two
Classification, Reinforcement and Repair, and Posting
A highly mobile Army will make use of existing bridges. Before using a bridge for military traffic, engineers must first determine if the bridge can safely support the loadings. For this purpose, the Army uses the MLC system. Several methods exist for determining a bridge's MLC, each with different degrees of complexity and accuracy. These methods are discussed in Chapter 3.
Often, existing bridges might be in need of repair due to years of maintenance neglect or war damage. Other bridges might be in good shape physically, but their load capacities (classifications) might be too low to support the military vehicles that must use them. Chapter 4 provides guidance for the repair of existing bridges and methods to upgrade the load capacity of typical bridges.
Once a bridge has been classified using the "analytical method" discussed in Chapter 3, signs must be posted on the bridge to inform users of its classification. Standard methods for posting bridges are provided in Chapter 5.
| This chapter implements STANAG 2021 (Edition 5) |
Chapter 3
Classification
A classification number is assigned to a given bridge to represent how much military vehicular traffic the bridge can carry. Width and height restrictions also affect a bridge's classification. A bridge might have a dual classification (such as for wheeled and tracked vehicles) when its capacity is greater than Class 50. The classification procedures presented in this chapter are based on guidance found in STANAG 2021. Other criteria (not covered by the STANAG) have been adopted from the AASHTO's Standard Specifications for Highway Bridges. Follow the same procedures in this chapter when analyzing foreign bridges, but be aware of and allow for any differences in material properties and design criteria.
| SECTION I - BRIDGE-CLASSIFICATION CONSIDERATIONS |
3-1. The two primary methods of classifying bridges are the expedient and the analytical. The analytical method is the most accurate and desirable. Between these two extremes are many combinations, some of which are discussed in this chapter. The classification method used will depend on the situation and the available time and information. A complete analytical classification might be needed if using a bridge is very important. Also, only the results from the analytical method can be posted and reported as a permanent load classification for a bridge.
3-2. Bridge reconnaissance is necessary for classification. Even if bridge plans are available, conduct an on-site inspection to ensure the accuracy of the bridge data. If key bridges are behind enemy lines, perform reconnaissance by long-range patrols or aerial photography. Local civilians are a valuable source of information and should not be overlooked during on-site reconnaissance. See FM 5-170 for more information on conducting a bridge reconnaissance.
3-3. Engineer units are responsible for gathering and maintaining bridge-classification data for bridges in their areas. These units report this information to higher engineer echelons for consolidation and distribution. As-built plans are included as part of the bridge-classification data.
3-4. Local highway authorities are the most important source of bridge-classification information. In most jurisdictions, these authorities maintain as-built plans and information on material properties of the bridges. Local, state, and country officials in the US and most foreign countries often impose maximum load limits or permissible stresses on their bridges. It is very important that military units consult local officials when determining the maximum MLC of a bridge intended for use during peacetime maneuvers. If they do not, the provisions of STANAG 2021 and this chapter will govern bridge classification.
| SECTION II - EXPEDIENT CLASSIFICATION |
3-5. In some situations, an engineer's estimate based on an expedient method might be sufficient. The classifications resulting from an expedient method will be less accurate as well as conservative. The expedient method chosen will depend on the amount of bridge data and time available for conducting a classification.
HASTY METHOD
3-6. A hasty classification is the most expedient but inaccurate classification method. It is based on how many and what types of civilian vehicles cross a bridge regularly. This information can be obtained through reconnaissance, from local officials, or from observation of the type of route that the bridge is on (for example, rural road or secondary or major highway).
3-7. Once the type of civilian vehicles that use the bridge have been identified, it can be assumed that military vehicles of similar weight and axle configurations could also cross the bridge safely. In many cases, this method will severely limit the allowable military vehicles since many of them are much heavier than typical civilian vehicles. A more in-depth classification method will likely reveal that the bridge has a higher MLC than the hasty method indicates. Use the hasty method only when a rapid crossing is required. Do not post the resulting classification.
TRACK COMMANDER'S BRIDGE-CROSSING BOOKLET
3-8. Graphic Training Aid (GTA) 5-7-12 contains information for armor personnel to use in determining if a bridge is capable of carrying their vehicles. This method is very conservative; use it only during high-mobility operations. Do not post this rating.
| SECTION III - CORRELATION-CURVE CLASSIFICATION |
3-9. A direct correlation between known civilian design loads and an equivalent MLC can be made by equating the respective design criteria and the vehicle's load effects. The bridge's original design load can be determined from the following sources (listed in decreasing order of reliability):
- Civilian bridge-inspection reports.
- Original design drawings or calculations.
- Federal or local highway authority bridge-design standards.
- Route requirements.
- Reconnaissance on known civilian vehicle usage (similar to the hasty classification).
3-10. Besides knowing the original civilian design load, the bridge's span length must be known. Use the design load and the span length to determine a temporary MLC using the correlation curves shown in Figures 3-1 through 3-7.
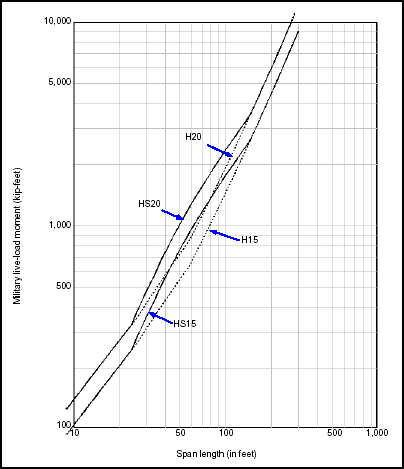
Figure 3-1. Correlation Curves for the United States
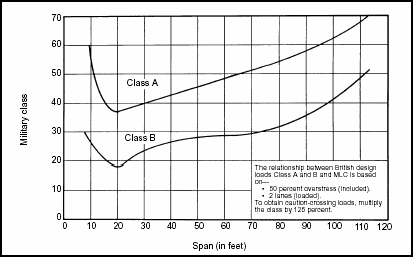
Figure 3-2. Correlation Classification for Civilian Bridges (British)
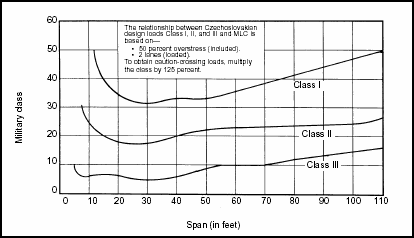
Figure 3-3. Correlation Classification for Civilian Bridges (Czechoslovakian)
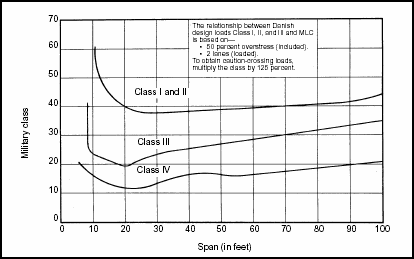
Figure 3-4. Correlation Classification for Civilian Bridges (Danish)
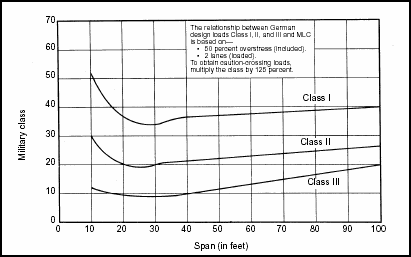
Figure 3-5. Correlation Classification for Civilian Bridges (German)
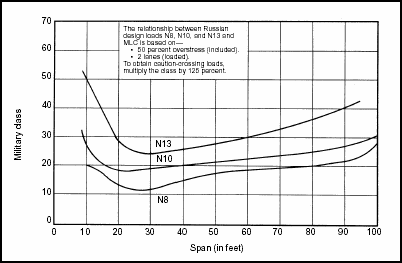
Figure 3-6. Correlation Classification for Civilian Bridges (Russian)
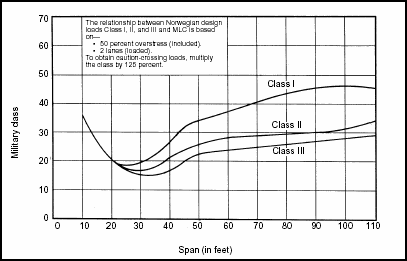
Figure 3-7. Correlation Classification for Civilian Bridges (Norwegian)
CORRELATION-CURVE APPLICATIONS
3-11. Only temporary MLCs are allowed with the correlation method. However, the method is soundly based on bridge-design theory and, when used properly, can result in a competent rating. Use these curves only on bridges that were designed using the appropriate design loadings and appropriate design criteria. Consequently, do not use the correlation-curve method on bridges in the back country or in third-world locations because careful design practices were probably not followed.
BRIDGE CONDITION
3-12. The correlation-curve method assumes that a bridge is in good condition (no significant deterioration). Because original bridge designs were probably conservative, allow for a small degree of deterioration before lowering the bridge's MLC. However, if the bridge appears significantly deteriorated, reduce the MLC accordingly. There are no firm guidelines to use when downgrading the MLC based on deterioration. However, a simple rule of thumb is as follows: if a member appears to have lost "X" percentage of its original cross section, reduce the computed MLC by the same percentage.
SPAN LENGTH
3-13. The correlation curves were developed for simply supported spans; however, other types of bridges can be classified by using the adjusted or equivalent span length. The adjusted or equivalent span length takes into consideration the positive moment on continuous or cantilevered spans. For truss, arch, and suspension bridges, apply the special considerations discussed below to determine the equivalent span length.
3-14. The correlation-curve method can be used for all bridge types. However, for truss and suspension bridges, use the procedure very carefully. If not careful and if using the wrong span length, the results could be too liberal for classification purposes. For each of these bridge types, determine the two span lengths as follows. After determining the truss span length and the panel length, use the lowest MLC rating.
- First span length. Follow the guidelines in paragraphs 3-15 through 3-17 (using the total span length) for all other types of bridges to determine the first span length. For single-span trusses, use the actual span length. For continuous-span trusses, use the equivalent span length (paragraph 3-42). For cantilever truss spans, use the span length of the suspended span. For steel-arch and suspension bridges, use the single longest span length.
- Second span length. Follow the guidelines in paragraphs 3-15 through 3-17 (using a span length equal to the stringers composing the floor system). These spans will be much shorter than those from the first span length. If stringer measurements are unavailable, use the following aids:
- For trusses, floor stringers are equal in length to the truss-panel lengths, which is the distance between intersections of truss diagonals. If panel lengths vary, use the longest.
- For steel arches, floor stringers are equal in length to the horizontal distance between the vertical supports running from the main arch to the bridge deck.
- For suspension bridges, floor stringers are equal in length to the horizontal distance between hanger cables, which are the vertical cables suspended between the main suspension cable and the bridge deck.
CORRELATION-CURVE USES
3-15. Once the span length has been determined, use correlation curves to determine the MLC. The process differs with US and foreign bridges.
UNITED STATES BRIDGES
3-16. Figure 3-1 shows the correlation curves for bridges in the US. The four standard classes of highway loading (as defined by AASHTO) used in the US are H15, H20, HS15, and HS20. The correlation curve that is used will depend on the year in which the bridge was designed and the route it is on. For newer or reconditioned bridges on major US highways, it will most likely be HS20. If unable to determine the original design load for older US bridges, the H15 curve can usually be used.
3-17. Locate the appropriate span length and the AASHTO loading on the graph, and read left to get the live-load moment. If the bridge normally carries two-way civilian traffic but a one-way MLC is needed (this will be higher than a two-way MLC and is used for caution crossings), multiply the live-load moment by the appropriate adjustment factor (K) from Table 3-1. Do not use the adjustment factor for a two-way MLC. Determine the live-load moment from Figure 3-1. Using this value of live-load moment along with the span length, determine the wheeled and tracked MLC from Table B-2. Adjust the MLC downward to account for width and height restrictions (see paragraph 3-44 for more information).
FOREIGN BRIDGES
3-18. Figures 3-2 through 3-7 show the correlation curves for other countries. Use the particular country's chart, locate the span length, and move up to intersect the appropriate bridge category. Then read the MLC from the scale on the left. These curves give a two-way MLC. For a one-way MLC, multiply the resulting MLC by the appropriate adjustment factor from Table 3-1.

| SECTION IV - ANALYTICAL BRIDGE CLASSIFICATION |
3-19. The analytical classification method is basically the reverse of the design method. In the design method, engineers establish the desired MLC and then determine the required size and quantity of bridge components to meet that MLC. In the analytical method, the bridge already exists and engineers must determine the composition, the dimensions, and the type of construction to obtain a permanent bridge classification. The analytical classification is based on classical methods of engineering analysis, but no rigid rules apply to the techniques used.
3-20. The difficulty of analytical bridge classification varies with the bridge type. The degree of accuracy depends on the information available, the techniques used, and the amount of detail covered. Some information gathering might be too difficult or time-consuming to be worth the effort. The engineer must make reasonable assumptions based on the information available. The classification techniques have been simplified as much as possible, consistent with good engineering practices, to permit a reasonably accurate bridge classification. Only qualified engineers should make permanent classifications.
CLASSIFICATION ASSUMPTIONS
3-21. The superstructure is almost always the controlling feature in bridge classification. Because the superstructure must span large distances, its elements must be made as lightweight as possible (designs must be optimized). This can be done effectively since superstructure loadings are fairly predictable. Substructures, however, must be more conservative (less efficient) in design to account for unpredictable loadings (stream and ice flow, barge impact) and unknown soil conditions. Do not check the substructure unless it appears to be significantly deteriorated or unstable due to scour or settlement, or is improperly designed or constructed.
CONTROLLING FEATURES
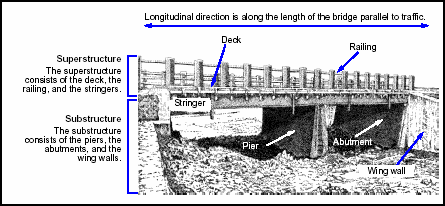
3-22. Figure 3-8 shows typical bridge components. The deck structure is generally stronger than its supporting superstructure; therefore, it is not considered in most classifications. The only exception to this rule is timber decking, which may be weaker than the rest of the superstructure.
Figure 3-8. Typical Bridge Components
3-23. Generally, connections are also stronger than the superstructure beams; therefore, they do not have to be considered in most classifications. The only exception is when a connection is deteriorated due to such factors as overstress or rust. In these cases, reduce the computed MLC (based on the superstructure beams) by an appropriate amount. If possible, study and document the connection carefully. Afterwards, an engineer can make a more accurate assessment of the connection's load capacity.
3-24. For bending-moment calculations on beams, assume the midspan to be the controlling location. The list below gives examples of where the midspan may not be the controlling location. Despite these possibilities, using midspan moments in all cases should give reasonable classifications.
- Steel girders with cover plates, where the worst case may be at the ends of the cover plates.
- Variable-depth plate girders, where the worst case may be at changes in the cross section.
- Reinforced concrete beams, where the worst case may be at bar cut-off points throughout the beam.
- Interior supports of continuous-span structures.
3-25. Bridges with longitudinal stringers may have smaller exterior stringers than interior stringers. The reason is because exterior stringers, by virtue of location, do not receive as much of the vehicular loading as interior stringers. For rating purposes, assume that the interior stringers control. This is a reasonable assumption since military convoy loadings are generally concentrated toward the center of a bridge. If this case does not occur, consider the capacity of the exterior stringers separately.
BRIDGE CONDITIONS
3-26. Classification procedures assume that a bridge is sound. Because original bridge designs are generally conservative, allow for a small degree of deterioration before reducing the computed classification. However, if the bridge appears significantly deteriorated, reduce the MLC accordingly. If a careful on-site inspection can be conducted, account for deterioration by reducing the cross-sectional dimensions of the members (or reinforcing steel) or by reducing material strengths. If an inspection is not possible, then compute the classification based on normal conditions and make conservative assumptions about the MLC to account for the deterioration.
MEASUREMENTS
3-27. Measure the spans of simply supported bridges from center to center of the supports. The supports may be bearing plates or rollers. In a multispan bridge, measure the weakest span for classification purposes. If not sure which spans to measure, measure and classify all of them. Measure the spans to the nearest 1/2 foot, always rounding up. Prepare sketches showing all the bridge's dimensions and cross sections that were used to classify it. For moment calculations, measure the cross-section dimensions at the midspan and indicate the complete details of the main structural component. For shear calculations, measure the cross-section dimensions near the span supports. If using as-built plans and specifications to classify a bridge, survey the bridge to verify the drawings and check the existing bridge conditions. For more information on bridge reconnaissance, see FM 5-170.
DEAD LOAD
3-28. The dead load is usually computed as a uniformly distributed load acting along the length of a member. Compute the dead load, based on member dimensions, using the typical weights shown in Table 3-2. Dead load consists of the weight of—
- The main structural members (stringers, girders, or trusses).
- The decking.
- All accessories and hardware (curbs, handrails, bracing, nails, and bolts).
3-29. The weight of a 1-foot length of the bridge span is computed to determine the uniform dead load. To compute the dead load, determine the weight per foot of all members supporting the loads and add it to the weight of all the bridge components carried by the members in a 1-foot length of the span. Equations 6-35 through 6-43 are simpler for determining the dead load. Next, compute the portion of the dead load that each member is carrying as follows:
|
|
|


LIVE LOAD
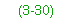
3-30. Vehicle loads are assumed to be the only live load acting on a bridge. The standard NATO vehicles in Appendix B are the vehicles that should be used to rate bridges. Assume the standard NATO convoy spacing of 100 feet between vehicles when rating. Because of this large spacing, usually only one vehicle will be on any single span of the bridge at a time. If significant pedestrian traffic is expected (refugees and dismounted military units), treat these as line loads of 75 pounds per foot, each over a 1-foot width. Place these line loads where the lines of people might be expected.
IMPACT LOAD
3-31. Increase the live loads by 15 percent to account for impact. Use this factor for all bridge types and span lengths except for timber-stringer or floating bridges. The impact on these bridges is zero.
LOAD DISTRIBUTION
3-32. Each structural component of a bridge shares, to varying degrees, in carrying the applied live loads. This load-sharing concept is accounted for in the bridge rating procedure by the number of effective stringers. The values in Table 3-3 are for longitudinal stringers and depend on the deck stiffness and stringer type and spacing. The specific use of these factors for different bridge types is discussed below. Distribution equations for other members (such as girders and trusses) are provided in their respective sections.

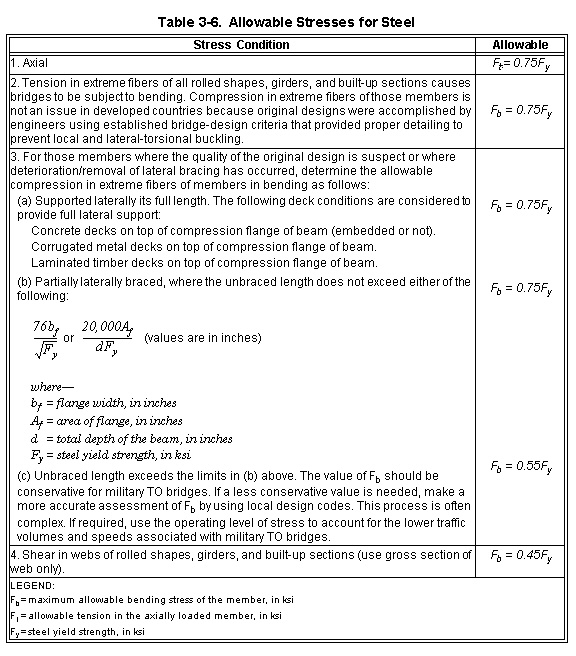
ALLOWABLE STRESSES
3-33. A load classification will only be as good as the definition of the material properties (for example, yield point or modulus of elasticity). Determine these properties as accurately as possible. Obtain accurate data from property testing (nondestructive testing, concrete cores, steel coupons), an original design, or as-built drawings/records. Once obtained, reduce the maximum material properties by specific amounts to obtain the safe usable portion of the property, referred to as the allowable stress. Allowable stresses based on deflection, bearing stress, and fatigue are not considered in this manual. The following list tells where to find allowable stresses and specific material properties for the different elements:
- Timber, paragraph 3-47.
- Steel, paragraph 3-63.
- Concrete, paragraph 3-132.
- Prestressed concrete, paragraph 3-164.
MOMENT CLASSIFICATION FOR SIMPLE SPANS
3-34. Compute the total moment capacity of the main structural component (stringer, girder, or floor beam) as follows:
|
|
|

DEAD LOAD AND DEAD-LOAD MOMENT OF A COMPONENT
3-35. Determine the portion of the dead load carried by the structural component (paragraph 3-28) and the dead-load moment that applies to that component. See Appendix D for concentrated dead loads. For uniformly distributed dead loads, use the following equation:
|
|
|

LIVE-LOAD MOMENT OF A COMPONENT
3-36. Compute the live-load moment of a component as follows:
|
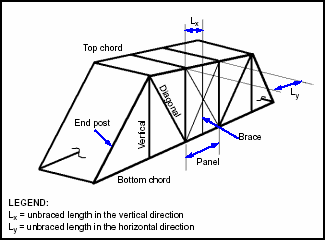
|
|

NUMBER OF EFFECTIVE COMPONENTS
3-37. Determine the number of effective components that support the live loads for one- and two-lane traffic. Each bridge-classification procedure addresses the number of effective bridge components.
TOTAL LIVE-LOAD MOMENT PER LANE
3-38. Compute the total live-load moment per lane as follows: :
|
|
|

MOMENT CLASSIFICATION FOR VEHICLES
3-39. Determine the moment classification for wheeled and tracked vehicles and for one- and two-lane traffic. To do this, use the hypothetical vehicle-moment tables or curves in Table B-2 or Figures B-1 or B-2.
MOMENT CLASSIFICATION FOR CONTINUOUS SPANS
3-40. Continuous-span bridges are often used for multispan bridge structures (Figure 3-9). This type of bridge results in a savings of material or in longer spans for the same amount of material when compared to a simply supported bridge. The efficiency of a continuous-span bridge lies in the principle that the total moment imposed on a bridge is distributed between positive moment at the midspan and negative moment over the continuous supports. Due to this redistribution of moment, a smaller bridge member (stringer, girder, truss) will be required to resist the moment caused by the applied loads. Figure 3-10 compares a simply supported and a continuous-span bridge.
Figure 3-9. Typical Continuous-Span Bridge
Figure 3-10. Comparison Between a Simple-Span and Continuous-Span Bridge
EQUIVALENT SPAN LENGTH
3-41. Continuous-span beams are always indeterminate. Therefore, accurate bending moments within the spans can only be determined by rigorous indeterminate analysis (such as moment distribution or matrix methods). Such an analysis is not practical in most situations; therefore, an expedient, yet reliable, method is needed. Ordinary continuous-span bridges can be rated approximately, using the concept of an equivalent simple span. A simple span is often thought of as the distance between the live-load inflection points on a continuous-span bridge. Actually, the equivalent span length is the length of a simple span that would receive the same maximum live-load moment that would be produced on a continuous span by the same loading.
3-42. The equivalent simple-span length is 0.80 times the length of the end span or 0.70 times the length of the interior span. If a bridge has all equal span lengths, analyze the exterior span. If a bridge has various span lengths, analyze the span that results in the longest equivalent span length. The applicability of these factors decreases for bridges with spans greater than 90 feet or with large differences in the cross section or the span length. In these cases, consider using a more in-depth indeterminate analysis.
FINAL CLASSIFICATION
3-43. After selecting the controlling span and its equivalent span length, classify the bridge the same as a simply supported span. Note that for this situation, use the equivalent span length for calculating dead-load moment. Obtain the live-load moment from the tables and curves in Appendix B.
ROADWAY-WIDTH CLASSIFICATION AND CLEARANCE RESTRICTIONS
3-44. Minimum roadway-width restrictions shown in Table 3-4 are based on NATO military-vehicle classifications (see STANAG 2021). If a bridge with a specific classification meets these width requirements, all standard military vehicles bearing the same or lower classification may cross the bridge. If a one-lane bridge meets all the requirements except the minimum width, post a width restriction without downgrading the classification. Two-lane bridges must meet the requirements in Table 3-4. If necessary, downgrade the two-lane classification for width requirements. The desirable minimum overhead clearance for bridges is 14 feet 9 inches. Post a clearance-restriction sign and a telltale for bridges not meeting overhead-clearance requirements. Posting requirements are discussed in Chapter 5.

SOLID-SAWN AND GLUE-LAMINATED TIMBER-STRINGER BRIDGES
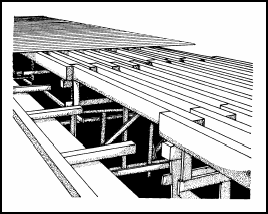
3-45. Timber-stringer bridges (Figures 3-11 and 3-12) are very common because they are often more economic and expedient than steel or concrete bridges. The timber may be native or dimensioned or glue-laminated sections. The spans are usually simply supported and rarely exceed 20 feet. The decks are either plank or laminated timber. Some civilian bridges may have asphalt wearing surfaces, which will significantly affect the dead load on the bridge.
Figure 3-11. Timber-Stringer Bridge
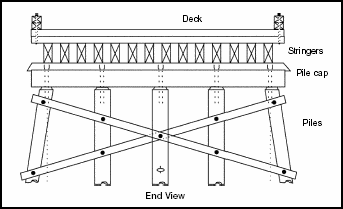
Figure 3-12. Timber-Stringer Bridge Components
3-46. The kinds and qualities of timber vary greatly, depending on such factors as geographic location, age, load history, defects, and moisture content. If the species and grade of the timber are known (as-built or design drawings), use the allowable stresses from Table C-1 or the design drawings (if provided). In most cases for military loadings, these values may be increased by a factor of 1.33 to account for lower traffic volume (shorter cumulative load duration, which is significant for timber). Do not apply this factor for nonengineered bridges. Apply other modification factors to the allowable stress to account for such variables as lumber thickness/width ratios, edgewise or flatwise use, repetitive member use, and moisture content (see Table C-1 notes). In most cases, timber decking and stringers will retain moisture on their horizontal surfaces and should be considered in wet-service conditions as shown in Table C-1 .
3-47. If the species and grade of the timber cannot be determined, use Table C-2 to get allowable moments and shears or compute them using assumed values. For solid-sawn timber, assume the allowable bending stress to be 1.75 ksi and the allowable horizontal-shear stress to be 0.095 ksi. For glue-laminated timber, assume the allowable bending stress to be 2.66 ksi and the allowable horizontal-shear stress will be 0.200 ksi. Do not apply the increase factor of 1.33 (as discussed above) to these assumed values. However, apply the adjustment factors listed from the Table C-1 notes.
TIMBER DEFECTS
3-48. Use extreme care when classifying timber-stringer bridges. Stringers and bents are subject to rot and insect attack, especially in areas where they come into contact with the ground. In tropical or wet areas, fungus or other biological growth may weaken timber stringers considerably. Adjust the cross-sectional dimensions of the member to allow for this type of damage.
STRINGER MOMENT-CLASSIFICATION PROCEDURE
3-49. Determine the moment classification of the stringers (paragraph 3-34) using the allowable bending stress (paragraph 3-46) and the value for the number of effective stringers from Table 3-3. For one- and two-way traffic, compute the moment classification twice, using the appropriate values for each way.
STRINGER SHEAR-CLASSIFICATION PROCDURE
3-50. Timber is relatively weak in horizontal shear. Always check the shear capacity. Determine the allowable shear stress as discussed in paragraphs 3-46 and 3-47.
Shear Capacity per Stringer
3-51. Compute the shear capacity per stringer as follows:
|
|
|

Applied Dead-Load Shear per Stringer
3-52. Compute the dead-load shear per stringer as follows:
|
|
|

Live-Load Shear Capacity per Stringer
3-53. Compute the live-load shear capacity per stringer as follows:
|
|
|

Total Live-Load Shear for One or Two Lanes
3-54. For wheeled and tracked vehicles on solid-sawn timber bridges and for wheeled vehicles on glue-laminated bridges, use the following equation:
|
|
|

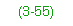
3-55. For tracked vehicles on glue-laminated stringer bridges, use the equations below:
Shear Determination
3-56. Using the value for the allowable vehicle shear (equations 3-9, 3-10, or 3-11), refer to Table B-3 or Figures B-3 or B-4, and find the MLC that produces a shear less than or equal to this value. If considering both one- and two-way traffic, compute twice, using the appropriate values for each way.
DECK CLASSIFICATION
3-57. Timber decks are either plank (wide dimension, laid horizontal with no interconnection between the planks) or laminated (wide dimension, laid vertical with the boards nailed or glued together). If timber decks control the load rating, check them.
Plank Decking
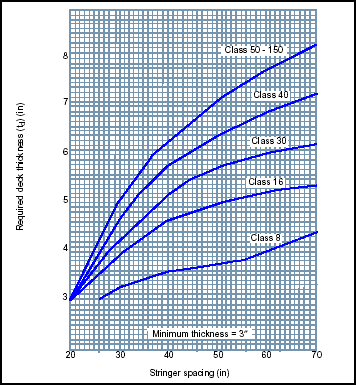
3-58. Use Figure 3-13 to determine the deck classification. Read the deck thickness on the vertical axis and the stringer spacing on the horizontal axis. Interpret the values between the curves, if necessary. For multilayer plank decking, subtract 2 inches from the total deck thickness. Then use Figure 3-13 to find the deck classification the same as for single-layer decks.
Figure 3-13. Timber-Deck Classification
Laminated Plank
3-59. Laminate the deck material to interconnect the adjacent boards in shear and allow them to share in the applied loadings more effectively. As a result, the applied wheel loads are effectively spread out to more deck boards than with a conventional plank deck. This increases the deck's rating over that of a plank deck with the same thickness.
3-60. For load-rating purposes, lamination indirectly has the effect of shortening the deck span between stringers by about 25 percent. Therefore, if the deck is effectively laminated (well nailed or glued over the full length of the boards), multiply the actual stringer spacing by 0.75, and use Figure 3-13 to find the deck classification.
WIDTH AND FINAL CLASSIFICATIONS
3-61. Check the width restrictions (paragraph 3-44 and Table 3-4). The lowest of the moment, shear, deck, or two-lane width classifications is the bridge's final classification.
STEEL-STRINGER BRIDGES
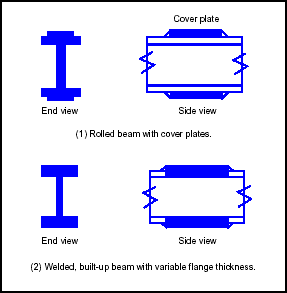
3-62. Steel stringers may consist of standard rolled shapes (more common in spans that are less than 100 feet) or of built-up sections from welded, bolted, or riveted steel plates (which are used for longer spans). Figure 3-14 shows a steel-stringer bridge. Rolled and built-up stringers may have cover plates in areas of maximum positive and negative moment (Figure 3-15). These plates increase the beam's section modulus and thus increase the allowable load. Because of the highly varied dimensions and details associated with steel-stringer bridges, accurate analytical classification of steel-stringer bridges is difficult without complete design or as-built data.
Figure 3-14. Steel-Stringer Bridge
Figure 3-15. Typical Steel Stringers
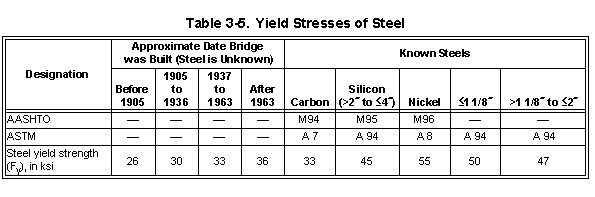
YIELD AND ALLOWABLE STRESSES
3-63. Allowable stresses are always given as percentages of the yield strength of steel. Consider the following:
- If the bridge's design or as-built drawings are available, the yield strength should be listed.
- If the yield strength is unknown, use the recommended values in Table 3-5.
- If the steel type or the date the bridge was built is not known, use 30 ksi.
Once the yield strength is determined, determine the allowable stresses using Table 3-6.
STRINGER MOMENT-CLASSIFICATION PROCEDURE
3-64. Compute the moment classification of the stringers (paragraph 3-34). Use the allowable bending stress (paragraph 3-63) and the appropriate value for the number of effective stringers from Table 3-3. If considering both one-way and two-way traffic, compute twice, using the appropriate values for each way. To classify built-up stringers, use the dimensions of the beam at the center of the span (the point of maximum positive moment).
DECK CLASSIFICATION
3-65. Decks distribute the live load to the stringers. Decks do not contribute to the moment capacity of the steel stringers unless composite construction is used. Reinforced concrete and steel-grid decks are used in civilian construction. Both decks are seldom critical in bridge classification. Classify timber decks as outlined in paragraph 3-57.
WIDTH AND FINAL CLASSIFICATIONS
3-66. Check the width restrictions (paragraph 3-44 and Table 3-4). The lowest of the moment, deck, or two-lane width classifications is the bridge's final classification.
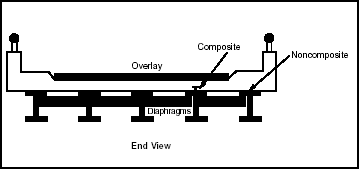
COMPOSITE-STRINGER BRIDGES
3-67. Composite-stringer bridges are difficult to recognize or distinguish from noncomposite steel-stringer bridges. If in doubt, classify the bridge as a noncomposite steel-stringer bridge, which results in a more conservative classification. Appendix F contains classification examples.
COMPOSITE -BEAM ACTION
3-68. When structurally connected, the concrete deck and steel stringer form a composite beam. Figure 3-16 shows a typical composite beam using a standard rolled beam and cover plate. The top flange takes maximum advantage of the compressive strength of the concrete deck. The bottom flange and cover plate are efficiently used in tension. Shear connectors or studs connect the concrete to the steel stringer and resist the horizontal shear forces between the concrete and the top flange.
Figure 3-16. Composite-Beam Section
SUPPORTED AND UNSUPPORTED CONSTRUCTION
3-69. During construction, steel beams are placed on the supports with cranes. The concrete-deck formwork is then constructed on top of these beams and the concrete deck is poured. During the deck placement, the steel beams may or may not have beam shoring along their length (supported or unsupported). If the beams are shored (supported) until the concrete of the deck cures, the resulting composite beam will be effective for the entire dead load of both the beam and slab, as well as live loads. If the beams are unshored (unsupported) during construction, then the steel beam by itself must support its own dead load, and the composite beam section will only be effective for the dead load of the deck and live loads. Normally, the cost of shoring is not practical when compared with the small increase in material costs required for unsupported construction. Unless the method of construction is definitely known, assume that unsupported construction methods were used. The analytical procedure shown below makes this assumption.
MOMENT-CLASSIFICATION PROCEDURE
3-70. The total moment that the composite beam resists, assuming unsupported construction, has two parts. They are the dead-load moment (that the steel beam alone resists) and the live-load moment (that the composite beam resists).
Dead-Load Moment
3-71. Determine the dead-load moment per stringer (paragraph 3-35). Note that the stringer must carry its own weight plus the weight of a portion of the concrete deck.
Stringer Section Modulus
3-72. Determine Ssteel, which is the section modulus for the steel stringer by itself. Refer to Table D-2.
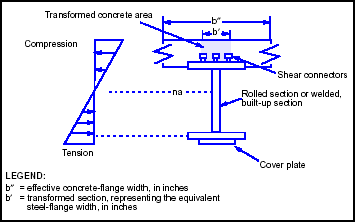
Effective Concrete-Flange Width
3-73. The effective width of the concrete flange is the lesser value of the following:
- One-fourth the span length, in inches (reduce the span length by 20 percent for continuous spans).
- Twelve times the concrete-flange thickness, in inches.
- The center-to-center stringer spacing, in inches.
Equivalent Steel-Flange Width
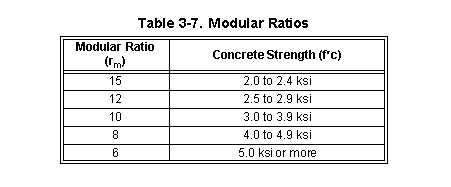
3-74. The concrete-flange width is represented as an equivalent steel-flange width for section-modulus calculations. Compute the equivalent steel-flange width as follows:
|
|
|

Section Modulus of Composite Section
3-75. Compute Scomposite, which is the section modulus of the entire composite beam (including the concrete deck) with respect to the bottom of the stringer. Use the methods described in paragraph D-14 to compute the section modulus or use the value from Table D-8.
Stress Due to Dead Load
3-76. Compute the stress induced in the steel by the dead-load moment as follows:
|
|
|

Live-Load Moment per Stringer
3-77. Compute the live-load moment per stringer as follows:
|
|
|

Final-Moment Determination
3-78. Use the procedure shown in paragraph 3-34 to compute the remainder of the moment classification.
WIDTH AND FINAL CLASSIFICATIONS
3-79. Check the width restrictions (paragraph 3-44 and Table 3-4). The lowest of the moment, deck, or two-lane width classifications is the bridge's final classification.
STEEL-GIRDER BRIDGES
3-80. A steel-girder bridge consists of two main flexural members (girders) that are built from steel plates. In older bridges, the members are built up with riveted plates and angles and a floor beam supports the stringers and the deck. In some cases, stringers are omitted and the floor beams alone transmit deck loads to the girders. For load-classification purposes, check the capacities of the deck, the stringers, the floor beams, and the girders. The limiting values will determine the load classification. Figure 3-17 shows a girder bridge. Figure 3-18 shows a through- and a deck-girder bridge. Figure 3-19 shows the main components of a girder bridge. Appendix F contains classification examples.
Figure 3-17. Girder Bridge
Figure 3-18. Girder Bridges
Figure 3-19. Girder-Bridge Components
YIELD AND ALLOWABLE STRESSES
3-81. Determine the yield and allowable stresses as shown in Table 3-6. This applies to all girder-bridge components discussed in the paragraphs below.
GIRDER CLASSIFICATION
3-82. Using the values below, determine the girder moment classification. If the girders are of composite construction, use the procedure in paragraph 3-70. Compute the yield and the allowable stresses from Table 3-6. Because there are no other checks required for steel girders (for example, shear), the resulting moment classification will be the only one.
Effective Number of Girders for One-Lane Traffic
3-83. Compute the maximum effective number of girders for one-lane traffic as follows:
|
|
|

Effective Number of Girders for Two-Lane Traffic
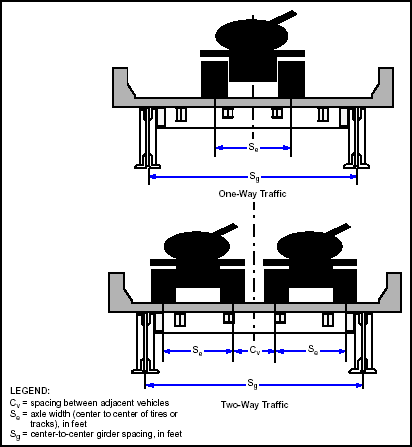
3-84. Figure 3-20 shows assumed loading conditions for normal two-lane bridges. Compute the number of girders for two-lane traffic using equations 3-16 and 3-17 .
|
|
|

|
|
|

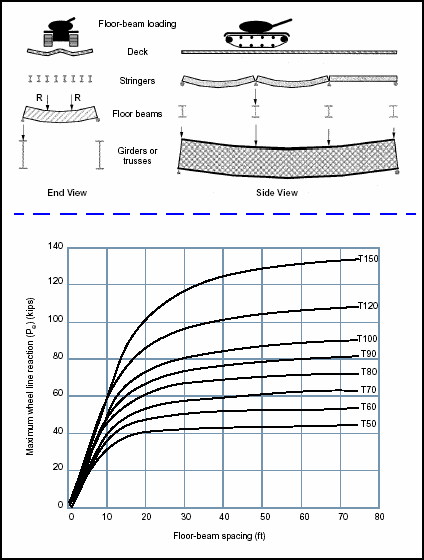
Figure 3-20. Assumed Loading Conditions for Maximum Moment in Floor Beams
3-85. For bridges with more than two lanes, the value of the minimum spacing between vehicles in adjacent lanes will generally be too conservative. In these cases, an engineer should determine the spacing requirement based on the—
- Actual curb-to-curb width.
- Expected travel lanes for the convoys.
- Presence of median strips and convoy speed.
- Degree of traffic control.
Total Moment Capacity per Girder
3-86. Compute the total moment capacity of one girder as follows:
|
|
|

Dead Load per Girder
3-87. Use equations 3-19 through 3-21 to compute the various components of the uniform dead load per girder and use equation 3-22 to compute the total dead load per girder:
|
|
|

|
|
|

|
|
|

|
|
|

Dead-Load Moment per Girder
3-88. Compute the dead-load moment per girder as follows:
|
|
|

Live-Load Moment per Girder
3-89. Compute the live-load moment per girder as follows:
|
|
|

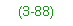
Total Live-Load Moment per Lane
3-90. Compute the total live-load moment per lane as follows:
|
|
|

Moment Classification
3-91. Determine the moment classification for both wheeled and tracked vehicles and for one- and two-lane traffic. Use the hypothetical vehicle-moment tables or curves in Table B-2 or Figures B-1 or B-2.
STRINGER MOMENT CLASSIFICATION
3-92. The stringers of a girder bridge act as a subspan that span the gap between the floor beams. The stringers are assumed to be simply supported with a span length equal to the center-to-center floor-beam spacing. Determine the stringer moment classification using the procedure found in paragraph 3-64 for noncomposite construction and paragraph 3-70 for composite construction. Compute the uniform dead load per stringer as follows:
|
|
|

STRINGER SHEAR CLASSIFICATION
3-93. Shear will seldom be critical if the stringers sit on top of the floor beams. However, if the stringers are connected to the floor beams by bolts or rivets, check for shear as follows:
- Shear capacity per stringer.



- Dead-load shear per stringer.



- Live-load shear capacity per stringer.


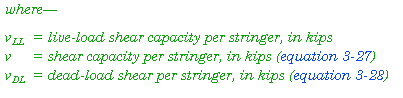
- Total live-load shear, one and two lanes.

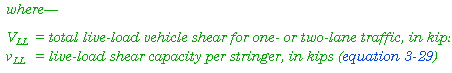
- Shear determination. Use Table B-3 or Figures B-3 or B-4 for classification.
FLOOR-BEAM MOMENT CLASSIFICATION
3-94. Floor beams run perpendicular to the line of traffic (Figure 3-19). Do not confuse these beams with stringers. The loading transmitted to a floor beam is a function of the span length (girder spacing), the floor-beam spacing, the dead load, and the weight and dimensions of the vehicles.
Total Moment Capacity of the Floor Beam
3-95. Compute the total moment capacity of the floor beam as follows:
|
|
|

Dead Load and Dead-Load Moment
3-96. The floor beam spans transversely across the bridge and supports the longitudinally spanning stringers and the deck above. Thus, in addition to its own self-weight, the floor beam must also support that part of the dead weight of the deck and stringers. Thus, compute the uniform dead load on the floor beam as follows:
|
|
|

and—
|
|
|

Live-Load Moment
3-97. Compute the live-load moment per component as follows:
|
|
|

Maximum Allowable Floor-Beam Reactions
3-98. Compute the maximum allowable floor-beam reactions as follows (also see Figure 3-20):
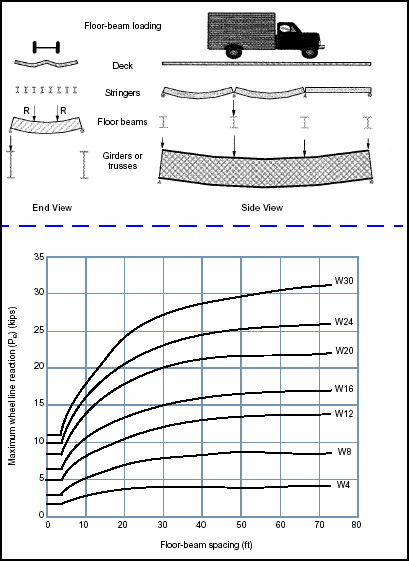
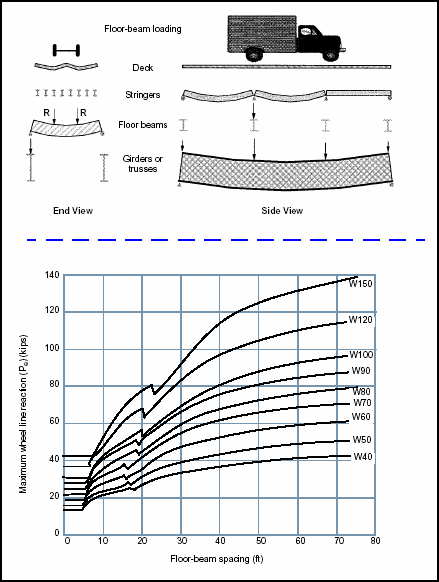
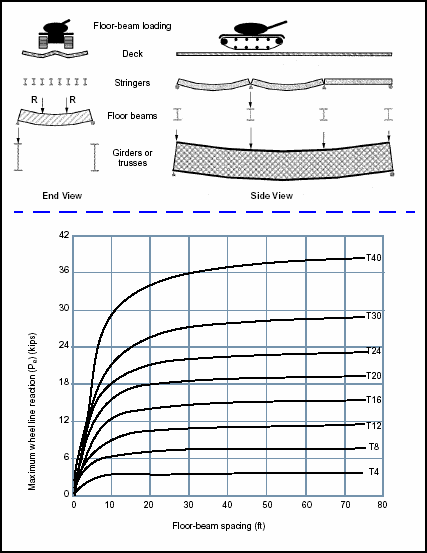
Moment Classification
3-99. To determine the moment classification, refer to the floor-beam reaction Figures 3-21 through 3-24. Find the vehicle MLC (wheeled or tracked) which produces a maximum allowable floor-beam reaction which is equal to or less than the computed values from equations 3-35 and 3-36.
Figure 3-21. Maximum Wheel Line Reactions for Wheeled Vehicles (W4-W30)
Figure 3-22. Maximum Wheel Line Reactions for Wheeled Vehicles (W40-W150)
Figure 3-23. Maximum Wheel Line Reactions for Tracked Vehicles (T4-T40)
Figure 3-24. Maximum Wheel Line Reactions for Tracked Vehicles (T50-T150)
FLOOR-BEAM SHEAR CLASSIFICATION
3-100. Shear will seldom be critical if the floor beams bear directly on the supporting girders (not connected via bolts or rivets). However, if the floor beams are connected to the girders by bolts or rivets, check for shear as described below.
Shear Capacity per Floor Beam
3-101. Compute the shear capacity per floor beam as follows:
|
|
|

Dead-Load Shear per Floor Beam
3-102. Compute the dead-load shear per floor beam as follows:
|
|
|

Live-Load Shear Capacity per Floor Beam
3-103. Compute the live-load shear capacity per floor beam as follows:
|
|
|

Maximum Allowable Floor-Beam Reactions
3-104. Compute the maximum allowable floor-beam reactions for one-way and two-way traffic as follows:
Special Allowance for Caution Crossing
3-105. If the load rating for shear needs to be higher than the rating that was computed from equations 3-40 and 3-41, compute a special caution-crossing allowance using the equations below. These equations will provide the highest possible rating for floor-beam shear. However, for these equations to be effective, the convoys must be carefully monitored on the bridge. The drivers must drive as close to the center of their respective lanes as possible. If they cannot do this, do not use these equations.
Shear Classification
3-106. Using the floor-beam reaction curves in Figures 3-21 through 3-24, find the MLC (wheeled or tracked) which produces a maximum allowable floor-beam reaction that is equal to or less than the computed values from equations 3-40 and 3-41. For caution situations, use equations 3-42 and 3-43.
DECK, WIDTH, AND FINAL CLASSIFICATIONS
3-107. Consider the following when determining deck, width, and final classifications:
- Decks distribute the live load to the stringers. Decks do not contribute to the moment capacity of the steel stringers unless composite construction is used. Reinforced concrete and steel-grid decks are used in civilian construction and are seldom critical in bridge classification. Classify timber decks as outlined in paragraph 3-57.
- Paragraph 3-44 and Table 3-4 apply to width restrictions.
- The final classification is the lowest of the girder, floor-beam, stringer, deck (if checked), or two-lane-width classification.
TRUSS BRIDGES
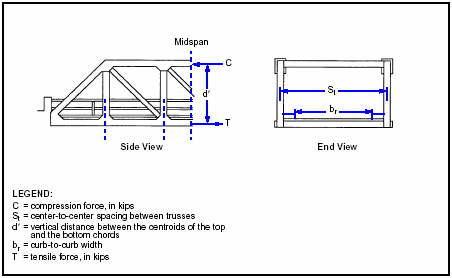
3-108. A truss (Figure 3-25) is a structure composed of straight members joined at their ends to form a system of triangles. It has the same function as the beams and girders and carries loads that produce bending moment in the structure as a whole. Many different types of trusses and truss combinations are used in long spans where beams and girders are not economical. These spans vary from 150 feet to over 1,000 feet. Some light truss bridges have simple spans as short as 60 feet.
3-109. Bending is resisted by the top chords in compression and the bottom chords in tension. Diagonals act as a web and resist shear. The end connections can be pinned, riveted, welded, or bolted. Pinned and riveted connections appear in the older structures, while the post-World War II structures have shop-welded and field-bolted connections.
Figure 3-25. Truss Nomenclature
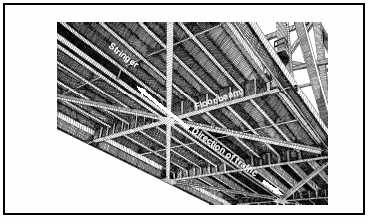
3-110. The floor system of a truss bridge (Figure 3-26) has floor beams that are connected at the panel points (intersection of diagonal truss members). The floor beams support floor stringers, which span between the floor beams and carry the load the same as those of a stringer bridge. For a proper analysis, the following types of truss and span configurations must be understood:
- Pony truss. A pony truss is a half-through truss that does not have an overhead bracing system and is normally used on relatively short spans (Figure 3-27).
- Through truss. A through truss is used for longer spans and has an overhead bracing system. Traffic passes through the truss (Figure 3-28).
Figure 3-26. Truss Floor System
Figure 3-27. Pony-Truss Bridge
Figure 3-28. Through-Truss Bridge
- Deck truss. A deck truss is used for longer spans and carries the traffic on the top chord (the truss system is below the bridge deck) (Figure 3-29).
Figure 3-29. Deck-Truss Bridge
TRUSS SPANS
3-111. Trusses can be continuous over their interior supports (Figure 3-30). Refer to paragraph 3-42 to determine the equivalent span length. Classify a continuous-truss bridge using the end span or the longest interior span, whichever controls.
Figure 3-30. Constant-Section Continuous-Truss Bridge
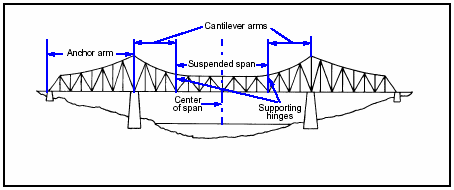
3-112. Most of the long-span truss bridges use cantilevered construction (Figure 3-31), which consists of two end spans and a suspended span. The end spans are anchored to the abutment by an anchor arm, and a cantilever arm projects from the pier. A suspended span is hinged to the two ends of and supported between the cantilever arms. This type of bridge should be classified using the suspended span, assuming that the suspended span is simply supported between the supporting hinges. In some cases, hinges are not used but the suspended span can be identified by the geometry of the bridge. The suspended span extends between 3/8 and 1/2 of the clear span between the piers.
Figure 3-31. Suspended Truss Span
EXPEDIENT CLASSIFICATION
3-113. A complete reconnaissance of a truss bridge can be very time-consuming. If time or access to the bridge is limited, a reasonable expedient classification can be achieved by considering only the floor system (stringers and floor beams [Figure 3-26]). The floor system of a truss bridge is the same as that of a steel-girder bridge. Refer to paragraphs 3-92 through 3-106 to rate the stringers and floor beams. If a quicker classification is needed, use the correlation-curve method (pay close attention to the span-length requirements of paragraphs 3-13 and 3-14).
ANALYTICAL CLASSIFICATION PROCEDURE
3-114. The analytical classification of a truss bridge consists of classifying the truss on the basis of positive moment capacity of the truss and checking the capacity of the floor beam and floor stringers.
Total Dead Load
3-115. Dead-load computations on a truss bridge can be rather lengthy, because it has many differently sized members. If possible, determine the actual dead load of the bridge by its individual components. Do this by—
- Analyzing each panel.
- Adding all of the weights of the components for the total dead-load weight.
- Dividing the total dead-load weight by the length of each panel.
3-116. If the above method cannot be used, use one of the following equations and Figure 3-32, to compute the total dead load of the bridge:
Figure 3-32. Truss Dimensions
Dead Load per Truss
3-117. Compute the dead-load weight per truss as follows:
|
|
|

Dead-Load Moment per Truss
3-118. Compute the dead-load moment per truss as follows:
|
|
|

Tensile Force in Bottom Chord
3-119. Compute the maximum allowable tensile force in the bottom chord as follows:
|
|
|

Compressive Force in Top Chord
3-120. Check the two different buckling coefficients as follows:
|
|
|
|
|
|

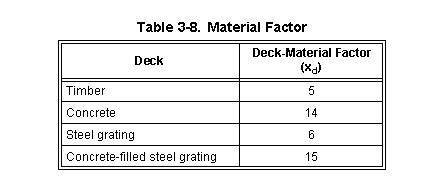
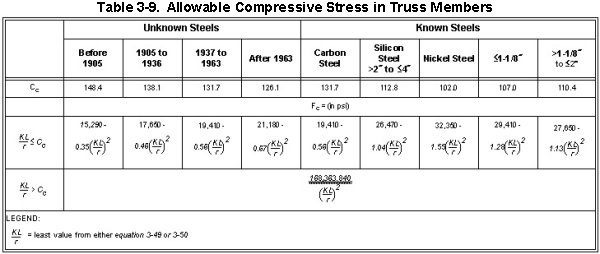
3-121. Table 3-9 gives the allowable compressive strength in truss members (in pounds per square inch [psi]). Divide the answer by 1,000 to get the ksi for use in equation 3-51. Use the larger KL/r coefficient from equation 3-49 or 3-50 and compare it to the appropriate buckling coefficient (denoted by Cc) in Table 3-9. Note that the value of Cc depends on the steel type and the yield stress. Use the appropriate equation from Table 3-9 to compute the allowable compressive stress (denoted by Fc).
|
|
|

Moment Capacity per Truss
3-122. Compute the total moment capacity as follows:
|
|
|

Live-Load Moment
3-123. Compute the live-load moment per truss as follows:
|
|
|

Effective Number of Trusses
3-124. Compute the maximum effective number of trusses for one-lane and two-lane traffic as follows:
- One-lane traffic.

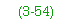

- Two-lane traffic. First compute—



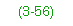

- Bridges with more than two lanes. The value of the minimum spacing between vehicles in adjacent lanes will generally be too conservative. An engineer can determine the spacing based on the actual curb-to-curb width, expected travel lanes for the convoys, the presence of median strips, the convoy speed, and the degree of traffic control.
Total Live-Load Moment per Lane
3-125. Compute the total live-load moment per lane as follows:
|
|
|

Truss Moment Classification
3-126. Determine the truss classification, based on bending moment, for both wheeled and tracked vehicles and for one- and two-lane traffic. Use Table B-2, or Figures B-1 or B-2. For simply supported trusses, use the actual span length. For continuous or cantilever trusses, use the span length as discussed in paragraph 3-111.
Stringers and Floor Beams
3-127. Determine the classifications of the stringers and floor beams using the same procedure as that for girder bridges in paragraphs 3-92 through 3-106. Check the bending moment and the shear capacity.
Deck Classification
3-128. Decks distribute the live load to the stringers. They do not contribute to the moment capacity of the steel stringers unless composite construction is used. Reinforced concrete and steel-grid decks are used in civilian construction. Both decks are seldom critical in bridge classification. Classify timber decks as outlined in paragraph 3-57.
Width and Clearance Restrictions and Final Classification
3-129. Check width restrictions as discussed in paragraph 3-44 and Table 3-4. Through-truss bridges have overhead bracing and require overhead clearance consideration. The final classification is the lowest of the girder, floor beam, stringer, deck (if checked), or two-lane-width classification.
REINFORCED CONCRETE SLAB BRIDGES
3-130. Concrete is very strong in compression and is a very efficient structural material. However, concrete is very weak in tension. Therefore, any concrete areas that may be subject to tensile stresses must be reinforced with steel reinforcing bars. Reinforced concrete slabs are often used for short-span bridges (Figure 3-33). Because of the highly varied dimensions and reinforcing details associated with reinforced concrete bridges, accurate analytical classification (as discussed later in this chapter) will be impossible without design or as-built details. If these are not available, use the other methods discussed in Sections II and III of this chapter.
Figure 3-33. Typical Reinforced Concrete Slab Bridge
ASSUMPTIONS
3-131. The analytical method (described later in this chapter) only applies to slab bridges with the main reinforcement running parallel to the direction of traffic. The slab acts as a one-way slab in the direction of traffic (Figure 3-34A). Assume that the area above the neutral axis acts in compression and that the reinforcing steel in the bottom of the slab carries all of the tension and the concrete carries no tension. The assumed stress distribution is shown in Figure 3-34B. Only the moment capacity is determined for the slab since shear generally will not control in thin, reinforced-concrete members. Only a one-foot-wide strip of slab at the midspan should be considered. For continuous spans, convert the span length to an equivalent span length as outlined in paragraph 3-41.
Figure 3-34. Details for a Reinforced Concrete Slab Bridge
CONCRETE STRENGTH
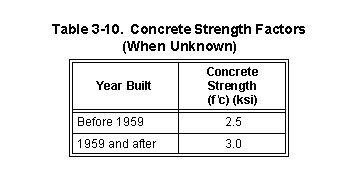
3-132. Try to obtain the ultimate strength of the in-place concrete from as-built drawings (listed on drawings as 28-day strength) or from concrete core tests. If this is not possible and the concrete is in satisfactory condition, refer to Table 3-10. If the year the bridge was built is unknown, use 2.5 ksi for the concrete strength.
REINFORCING STEEL STRENGTH
3-133. Try to obtain the yield strength of the reinforcing steel from as-built drawings. If this is not possible, use Table 3-11. If Table 3-11 does not show the needed yield strength, use 40 ksi for a bridge that appears relatively new and 33 ksi for a bridge that appears very old or deteriorated.
REINFORCING STEEL RATIO
3-134. Compute the reinforcing steel ratio as follows:
|
|
|

|
|
|

COMPRESSIVE-STRESS-BLOCK DEPTH
3-135. Compute the compressive-stress-block depth as follows:
|
|
|

SLAB MOMENT CAPACITY
3-136. Compute the moment capacity per foot width of slab as follows:
|
|
|

DEAD-LOAD MOMENT
3-137. Assume that the total dead load of the bridge, including the roadway and the curbs, is distributed over the full width of the slab. As shown in Figure 3-34A, the slab width may or may not equal the roadway width. Compute the dead-load moment as follows:
|
|
|

ALLOWABLE LIVE-LOAD MOMENT
3-138. For normal operating conditions, compute the allowable live-load moment per foot width of slab as follows:
|
|
|
For emergency conditions where a higher allowable loading is required, compute the live-load moment as follows:
|
|
|

EFFECTIVE SLAB WIDTH
3-139. Compute the effective slab width as follows:
|
|
|

TOTAL LIVE-LOAD MOMENT
3-140. Compute the total live-load moment for the entire slab as follows:
|
|
|

MOMENT CLASSIFICATION
3-141. Use the total live-load moment from equation 3-66 and the span length (adjusted for continuous span if necessary) with the moment values from Table B-2 or Figures B-1 or B-2 to determine the moment classification. The total live-load moment is the same for both one- and two-way traffic with this type of bridge. Therefore, two-way traffic will only be limited by the lane-width restrictions shown in Table 3-3.
REINFORCED CONCRETE T-BEAM BRIDGES
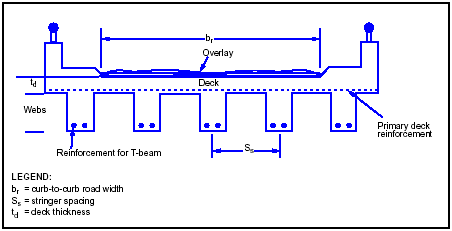
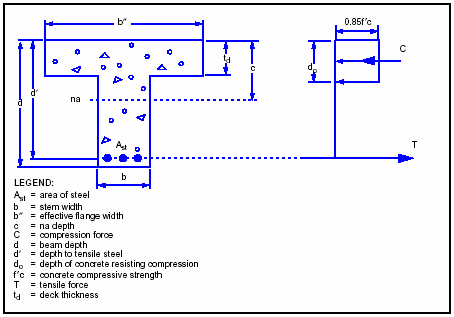
3-142. Figure 3-35 shows a typical reinforced concrete T-beam bridge. T-beams are used to obtain longer span lengths than those allowed by slab bridges (paragraph 3-130). The deck of the bridge acts integrally with and forms the top portion of the T-beam. The vertical leg of the T-beam (the stem) serves to position the reinforcing steel at a greater distance from the neutral axis. Because of the highly varied dimensions and reinforcing details associated with reinforced concrete bridges, accurate analytical classification (discussed below) will be impossible without design or as-built details. If these are not available, use the other methods discussed in Sections II and III of this chapter.
Figure 3-35. Reinforced Concrete T-Beam Bridge
ASSUMPTIONS
3-143. Figure 3-36 shows the assumed stress distribution of the T-beam. An analysis should be based on a typical interior T-beam. The exterior beams are assumed to have equal or greater capacity than the interior beams. As with the slab bridge, the T-beam bridge is analyzed only on the basis of moment capacity, which means shear will generally not control the rating. The deck is also assumed to have sufficient thickness that it will not control the rating and is thus not rated.
Figure 3-36. Assumed Stress Distribution in a T-Beam
CONCRETE AND REINFORCING STEEL STRENGTHS
3-144. For concrete and reinforcing steel strengths, refer to paragraphs 3-132 and 3-133.
EFFECTIVE FLANGE WIDTH
3-145. The deck width that carries the compressive stresses for an individual T-beam is the effective flange width and is the lesser of the following:
- One-fourth the span length, in inches (do not modify the span length for continuous spans).
- Twelve times the concrete-slab thickness plus the stem width, in inches.
- Center-to-center T-beam spacing, in inches.
TENSILE FORCE IN REINFORCING STEEL
3-146. Compute the tensile force in the reinforcing steel. First compute—
|
|
|

|
|
|

COMPRESSIVE-STRESS-BLOCK DEPTH
3-147. Compute the compressive-stress-block depth as follows:
|
|
|

MOMENT CAPACITY OF T-BEAM
3-148. If the compressive-stress-block depth is less than or equal to the concrete-deck thickness, compute the moment capacity as follows:
|
|
|

3-149. If the compressive-stress-block depth is greater than or equal to the concrete-deck thickness, determine the moment capacity. First compute—
|
|
|

|
|
|

|
|
|

|
|
|

DEAD-LOAD MOMENT
3-150. Assume the total dead load is distributed equally to each T-beam. The dead-load moment per T-beam would be as follows:
|
|
|

ALLOWABLE LIVE-LOAD MOMENT
3-151. For normal operating conditions, compute the allowable live-load moment on a single T-beam as follows:
|
|
|
For emergency conditions where a higher allowable loading is required, compute the live-load moment as follows:
|
|
|

TOTAL ALLOWABLE LIVE-LOAD MOMENT
3-152. Multiply the allowable live-load moment by the effective number of T-beams for one- and two-lane traffic to obtain the allowable live-load moment as follows:
|
|
|

MOMENT CLASSIFICATION
3-153. Use Table B-2 or the moment curves in Figures B-1 or B-2 to determine the moment classification. Compare the values of the total live-load moment and the span length (or equivalent span length if the span is continuous).
WIDTH AND FINAL CLASSIFICATIONS
3-154. Check the width restrictions in paragraph 3-44 and Table 3-4. The lowest of the moment or two-lane width classifications is the final bridge classification.
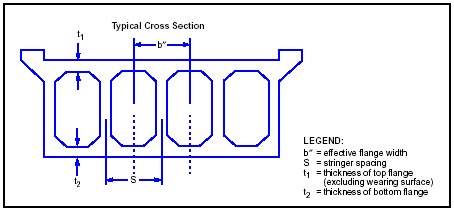
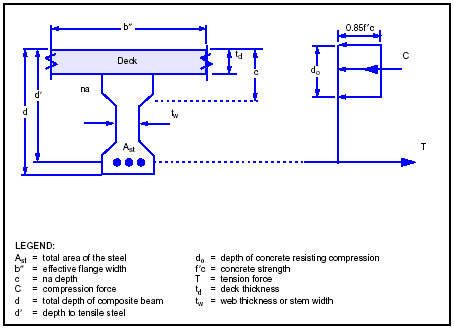
REINFORCED CONCRETE BOX-GIRDER BRIDGES
3-155. Reinforced concrete box-girder bridges (Figure 3-37) are used to acquire even greater span lengths than T-beam bridges. The deck of a box-girder bridge acts integrally with and forms the top portion of the thin-webbed I-shaped girders.
Figure 3-37. Typical Box-Girder Bridge
ASSUMPTIONS
3-156. The box-girder bridge is analyzed as a series of connected concrete I-beams, with flange widths equal to the spacing between the webs of the I-beams. As with T-beams, the exterior beams are assumed to have an equal or greater capacity than the interior beams. The box-girder bridge is analyzed only on the basis of moment capacity (shear will generally not control the rating). The deck is also assumed to have a sufficient thickness and a short enough span length so that it will not control the rating and is therefore not rated.
PROCEDURE
3-157. Use the same procedure as outlined for concrete T-beams in paragraph 3-143 to determine the classification of concrete box girders. Use the following equation to compute the effective flange width:
|
|
|

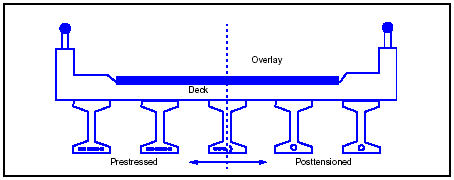
PRESTRESSED CONCRETE BRIDGES
3-158. Structural prestressing is placing a member in compression before it is loaded (Figure 3-38). This action is an improvement to conventional reinforced concrete. Normal concrete is very weak in tension and is very prone to cracking. Water penetrates the concrete and the concrete deteriorates. Prestressing prevents cracking under normal loads by placing the member's entire cross section in compression.
Figure 3-38. Conventional Reinforced Concrete Compared to Prestressed Concrete
RECOGNITION
3-159. There are many different forms of prestressed concrete beams, and they are sometimes difficult to distinguish from conventional reinforced beams. Compared to conventional beams, prestressed beams are usually precast and much more shapely than conventional poured-in-place beams. The most common form in the short- to medium-span ranges is the standard I-girder with a cast-in-place composite deck slab (Figure 3-39). Precast, pretensioned solid or voided slabs are used for shorter spans. Many long-span box-girder and T-beam bridges are also prestressed. Some bridges may be of segmental posttensioned construction (another form of prestressing).
Figure 3-39. Prestressed Concrete Bridges
COMPOSITE CONSTRUCTION
3-160. Prestressed beams are generally made composite with a concrete deck. This allows the deck to form a large part of the top flange of the beam. The roughened concrete surface and steel-shear reinforcement provide resistance to horizontal-shear forces between the deck and the precast beams. While it is very difficult to distinguish (visually) between composite and noncomposite construction, most prestressed construction is composite. Therefore, the analytical procedure discussed in this chapter assumes composite construction.
SUPPORTED AND UNSUPPORTED CONSTRUCTION
3-161. Precast, prestressed beams are placed on their supports with cranes during construction. The concrete-deck formwork is constructed on top of these beams and the concrete deck is poured. During the deck placement, the prestressed beams may or may not have beam shoring (supported or unsupported) along their length. If the beams are shored (supported) until the concrete of the deck cures, the resulting composite beam will be effective for the entire dead load of the beam and the slab, as well as live loads. If the beams are unshored (unsupported) during construction, the precast beam alone must support its own dead load and the composite beam will only be effective for the dead load of the deck and the live loads. Normally, the cost of shoring is not practical when compared with the small increase in material costs required for unsupported construction. Unless the method of construction is definitely known, assume unsupported construction. Therefore, the analytical procedure discussed in this chapter assumes unsupported construction.
LOAD-CLASSIFICATION METHODS
3-162. The analytical load-classification method gives the most accurate load classification. However, its use depends on complete details of the internal prestressing, which are generally not available without the original design drawings. If they are not available, use the other methods discussed in Sections II and III of this chapter.
ANALYTICAL CLASSIFICATION
3-163. If the interior and exterior beams are different, base the analysis on a typical interior beam. The exterior beams are assumed to have equal or greater capacity than the interior beams. Prestressed beams are analyzed on the basis of ultimate moment capacity, since shear will generally not control the classification. Also, the deck is assumed to have sufficient thickness that it will not control the classification and is thus not considered. The assumed stress distribution for prestressed beams is shown in Figure 3-40.
Figure 3-40. Assumed Stress Distribution in a Prestressed Beam
Concrete and Steel Strengths
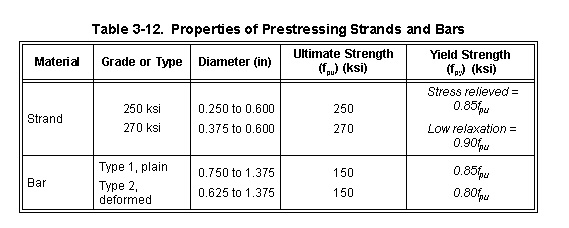
3-164. Prestressed beams may have a combination of prestressed and conventional nonprestressed steels. Obtain conventional reinforcing steel strengths as described in paragraph 3-133. Strength properties of prestressing can be obtained from the design drawings or from Table 3-12. Concrete strengths can be obtained from the design drawings or, if they are not known, use 4,000 psi.
Effective Flange Width
3-165. For T-beams or precast beams that are composite with the slab, the width of the deck that helps carry the compressive stresses for a beam is the effective flange width (Figure 3-40). The effective flange width is the lesser of the following:
- One-fourth of the span length, in inches (do not modify the span length for continuous spans).
- Twelve times the concrete-slab thickness plus the stem width, in inches.
- The center-to-center beam spacing, in inches.
Steel Reinforcement Ratios
3-166. Compute the steel reinforcement ratio (Figure 3-40). First compute—
|
|
|

|
|
|
|
|
|

Reinforcement Index
3-167. Compute the reinforcement index as follows:
|
|
|

Average Stress in Prestressed Steel
3-168. Compute the average stress in prestressed steel at maximum load as follows:
|
|
|

Maximum Tensile Force
3-169. Compute the maximum tensile force developed by a beam as follows:
|
|
|

Area of Concrete Resisting Compression
3-170. Compute the steel reinforcement ( Figure 3-40 ) as follows:
|
|
|

Area of the Concrete Flange
3-171. Compute the area of the concrete flange available to resist compression as follows:
|
|
|

Moment Capacity
3-172. Below are four equations used to compute the beam moment capacity. To choose the proper equation, compare the reinforcement index, the area of the concrete flange available to resist compression, and the area of the concrete resisting compression and then choose the equation for which all the comparisons are true.
- If Rr < 0.3 and Af > Ac, then—


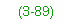

- If Rr < 0.3 and Af < Ac, then—

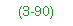
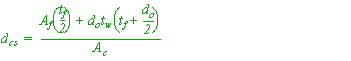
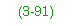

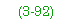

- If Rr > 0.3 and Af > Ac, then—

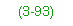

- If Rr > 0.3 and Af < Ac, then—
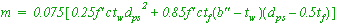
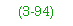

Dead-Load Moment
3-173. Assume the total dead load is distributed equally to each prestressed beam. The dead-load moment per beam would be computed as follows:
|
|
|

Allowable Live-Load Moment
3-174. Compute the allowable live-load moment as follows:
- For normal operating conditions, compute the allowable live-load moment on a single prestressed beam as follows:

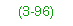
- For emergency conditions where a higher allowable loading is required, compute the live-load moment as follows:



Live-Load Moment per Lane
3-175. Compute the live-load moment per lane as follows:
|
|
|

Moment Classification
3-176. Determine the moment classification using the values of MLL and the span length (or an equivalent span length if the span is continuous). Refer to Table B-2 or Figures B-1 or B-2.
WIDTH AND FINAL CLASSIFICATIONS
3-177. Check the width restrictions in paragraph 3-44 and Table 3-4. The lowest of the moment or the two-lane width classification is the final bridge classification.
ARCH BRIDGES
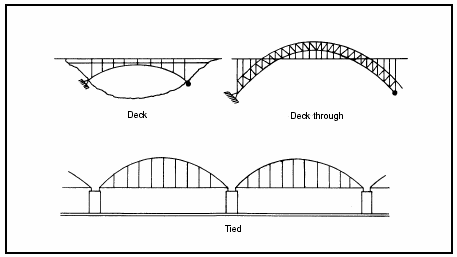
3-178. An arch is one of the most efficient structural shapes and one of the oldest methods of building relatively long spans. Some masonry-arch bridges that were built by the Roman legions are still in use today. Modern arch bridges are constructed with reinforced concrete and steel. Figure 3-41 shows general types of arch bridges. The masonry arch is a form of the deck arch. Except for the masonry arch, all arches have a floor system just like a truss or girder bridge. The floor beams are connected to the arch at support points. The support points usually have vertical, column-type members that carry the floor-beam loads to the main arch members.
Figure 3-41. Types of Arch Bridges
Modern-Arch Bridge
3-179. The analytical classification procedure for masonry-arch bridges is presented below. A complete reconnaissance of other arch bridges can be very time-consuming, and an exact analysis of these bridges is very tedious and time-consuming. A reasonable classification can be achieved by only classifying the stringers and floor beams of the floor system (the same as for a girder bridge [paragraphs 3-92 through 3-106]). If an even more expedient classification is required, use the classification-by-correlation procedure discussed in Section III of this chapter (see paragraph 3-13 for span-length requirements).
Masonry-Arch Bridge
3-180. A masonry-arch bridge is very difficult to analyze accurately. An empirical formula that is based solely on the bridge's dimensions is provided below.
Provisional Load Classification
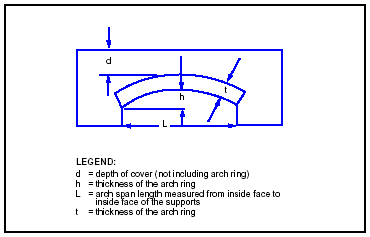
3-181. Measure the critical dimensions (arch span length and total crown thickness) of the bridge (Figure 3-42). Plot these dimensions on the nomograph in Figure 3-43 to determine the provisional load class (PLC). With a span length of 30 feet and a total crown thickness of 42 inches, use the nomograph as follows:
- Find the arch span length (denoted by L) in Column A.
- Find the total crown thickness (t + d) in Column B.
- Draw a straight line through the points in Columns A and B. The point at which the line intersects Column C is the PLC. For this example, the PLC is 96.
Figure 3-42. Critical Dimensions of a Masonry-Arch Bridge
Figure 3-43. Provisional Load Carrier for a Masonry-Arch Bridge
Military Load Classification
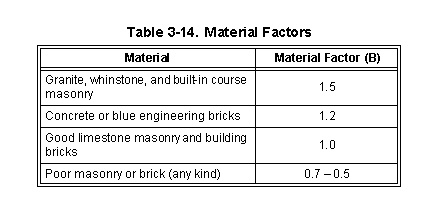
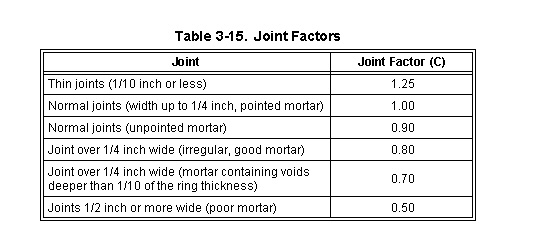
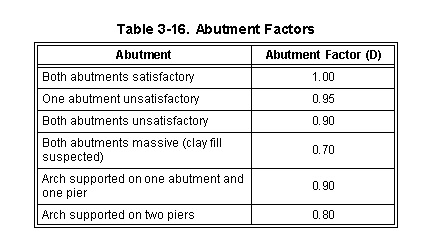
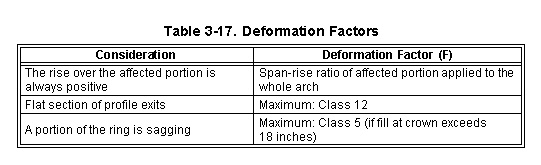
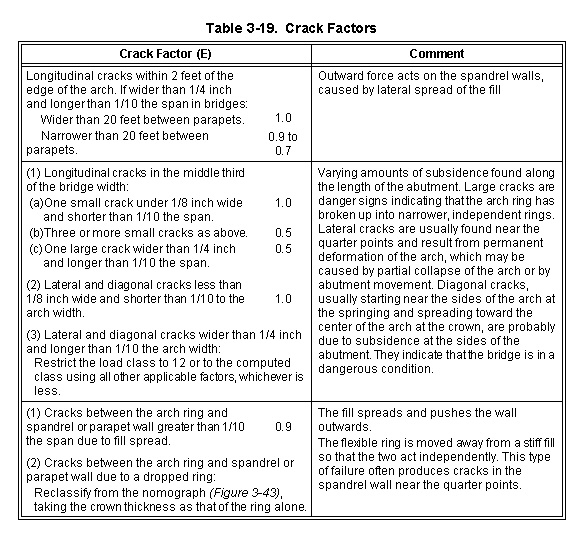
3-182. Obtain the one-lane, tracked MLC. Multiply the PLC by the appropriate bridge factors (Tables 3-13 through 3-19 and Figure 3-44) as follows:
|
|
|

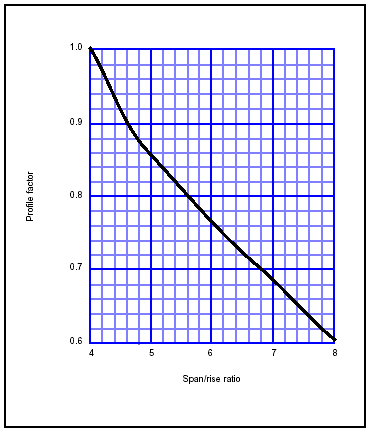
Figure 3-44. Profile Factors for Arch Bridges
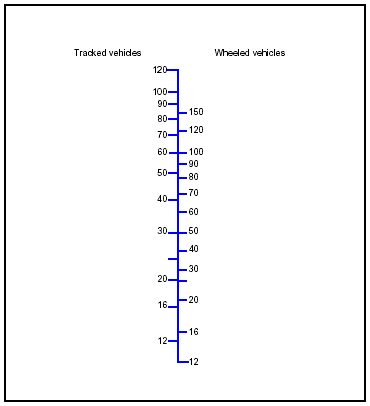
3-183. Apply the E, F, and G factors with discretion. For example, if an arch is deformed and cracked because of abutment faults, do not downgrade the bridge for all three factors. In such cases, apply the E, F, and G individually to the PLC, modified by A through D. Use the lowest of the three results as the one-lane MLC. If the bridge is wide enough for two lanes of traffic, multiply the one-lane MLC by 0.9 to get the two-lane MLC. Use Figure 3-45 to equate one- and two-lane, tracked classifications to respective wheeled classifications.
Figure 3-45. Bridge Classification Correlations
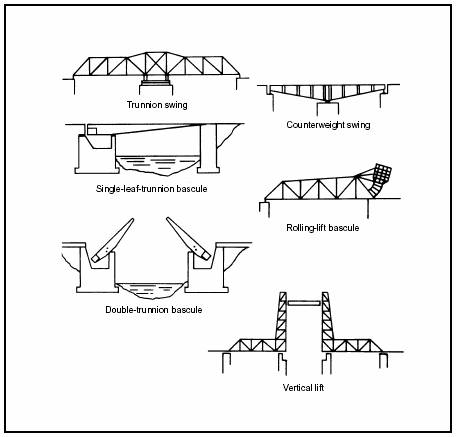
MOVABLE BRIDGES
3-184. When a highway crosses a navigable waterway with light boat traffic, movable bridges are often constructed as a cost-saving measure (Figure 3-46). The three general types of movable bridges are swing, bascule, and vertical-lift. Construction is usually a truss or girder system with machinery to move the bridge away from the navigation channel. Determine the MLC the same as for fixed bridges of the same type (girder, truss, and so on). The machinery/gearing for moving the bridge should have no effect on the MLC. Special warning signs should be posted indicating the presence of a movable bridge.
Figure 3-46. Typical Movable Bridges
SUSPENSION BRIDGES
3-185. A suspension bridge (Figure 3-47) is used mainly for long spans where support from below is impracticable (for example, when a water current is too swift or when the gap to be bridged is too deep). Most spans over 2,000 feet are of suspension construction. Like truss and girder bridges, all suspension bridges have a floor system consisting of stringers and floor beams. The floor beams are connected to the suspension cables at hanger points.
Figure 3-47. Typical Suspension Bridge
3-186. The load capacity of a suspension bridge may be based on many limiting elements, such as the support towers and the suspension cables, anchorages, and hangers. The reconnaissance and analysis effort for all of these elements would be very time consuming. A reasonable classification can be achieved by only considering the floor system (such as the stringers and floor beams that are suspended between the hangers [the vertical cables hung from the suspension cables]). The floor system of a suspension bridge is the same as that of a steel-girder bridge. Use paragraphs 3-92 through 3-106 to rate the stringers and floor beams. If a more expedient classification is required, use the classification by correlation procedure discussed in Section III of this chapter (pay careful attention to the span length requirements of paragraph 3-13).
OTHER BRIDGES
3-187. This section may not have covered all bridge types found in the TO (especially in foreign countries). Local civilian authorities are the best source for obtaining a reasonable MLC on these bridges; otherwise, an analysis of the superstructure will usually suffice.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|