K.5.0 UNCERTAINTIES IN HUMAN EXPOSURE ASSESSMENT
In addition to source terms and contaminant transport, exposure assessment contributes to uncertainty in the risk estimates. Some of the contributing parameters are lifestyle, diet, land use patterns, exposure pathways, exposure frequency and duration, and biotransfer/bioaccumulation factors. These uncertainties are discussed in the following sections.
Humans may be exposed to hazardous substances in many ways, which may cause some degree of risk to health. The uncertainty in risk for each receptor increases as the variety of potential exposures increases. The risk analysis in the TWRS EIS includes multiple exposure scenarios that cover a wide spectrum of exposure pathways. Therefore, the likelihood that real future exposures lie outside the range estimated in the EIS is small.
The post-remediation land user scenario describes the long-term risk to an individual and the whole population from restricted to unrestricted use of the land. The Native American and residential farmer receptors use land without any restrictions, and the industrial worker and recreational users use land with some limited restrictions. The health impacts of short-term exposure (routine and accidental) that would occur during remediation add a layer to the analysis that reduces the systematic uncertainties in the risk assessment. Another health impact, exposure to hazardous substances by inadvertent intrusion, characterizes a different exposure category.
The uncertainty in exposure assessment is more fully characterized by incorporating several exposure scenarios and categories. The uncertainties within each of these scenarios and categories are diverse and can be large. There is a need to analyze each scenario and category on an individual basis. The following sections discuss the uncertainty in the risk assessment for post-remediation land use, routine and accidental exposures during remediation, and post-remediation intrusion.
K.5.1 POST-REMEDIATION LAND USER
This section describes the uncertainty analyses for the risks to potential post-remediation land users. Scenarios evaluated under the post-remediation land user scenario include: the Native American, residential farmer, industrial worker, and intruder.
K.5.1.1 Modular Risk Assessment Approach
The method used to assess the post-remediation risk at the Hanford Site was a modular risk assessment (MRA) approach. The MRA approach separates the four basic components of the risk assessment (i.e., source, transport, exposure, and risk) into discrete modules that can be assessed independently and then combined. This process is described by the following equation:
Risk = Source Unit Transport Factor Unit Risk Factor
This section focuses on the results of the uncertainty and sensitivity analysis as they pertain to the unit risk factor (URF). The uncertainty analyses with respect to the source term and the unit transport factors are presented in other sections of this appendix.
The calculation of the URF is simplified by dividing the equation into two terms, one term containing parameters independent of contaminant properties (i.e., summary intake factors) and the other term containing parameters dependent on contaminant-specific properties.
URFs are described in terms of exposure pathways, toxic endpoint (carcinogenic chemical, noncarcinogenic chemical, and radionuclide carcinogen), and exposure parameters (i.e., intake rate, exposure frequency, and exposure duration). The URF approach involved structuring the intake equations for each receptor and exposure pathway so that contaminant-independent parameters were separated from the contaminant-specific parameters.
The pathway-specific slope factor is a toxicological contaminant-specific parameter that is specified by the regulatory agencies and generally not subjected to an uncertainty analysis, although there is considerable uncertainty associated with this parameter.
The intake term may be further described in terms of the following equation:

Where:
Intake = average daily intake of pollutant
C = concentration of pollutant
PF = pollutant-specific factor for media of concern
SIF = summary intake factor for given scenario
The uncertainties associated with the concentration term and other pollutant-specific factors are discussed in other sections of this appendix. The uncertainty associated with the SIF or intake term is the subject of this section of the report.
The SIF is a scenario-specific term and generally is derived from exposure factors published by the EPA for generating upper-bound (i.e., 95th percentile) point estimates of exposure. The use of these upper-bound estimates in calculating point estimates for human health exposure has been shown to result in "compounding conservatisms," which often has led to risk estimates that are highly unlikely to be experienced by anyone in a population near a site (Burmaster-Harris 1993). Therefore, a knowledge of the uncertainty associated with the SIF and exposure factors used to generate risk estimates is important to place the risk estimates in perspective.
One approach for establishing the uncertainty in the SIF and exposure parameters is to use a Monte Carlo-based approach (PNL 1993). In this approach, the Monte Carlo technique adds several steps to estimate both point values and full distributions for the exposures. These extended techniques make the analyses more informative to risk managers and members of the public by giving some perspective on the uncertainty behind the point estimates.
K.5.1.2 Monte Carlo Uncertainty Analysis
The first step in the Monte Carlo uncertainty analysis was to identify the exposure medium (air, soil, groundwater) and exposure pathway (e.g., ingestion, inhalation, vegetable consumption) driving the risk. The next step involved constructing equations that would both represent the shortcomings identified in EPA methodology and correspond with the site-specific conditions. These preliminary equations were used, along with readily available input ranges, to conduct a sensitivity analysis to determine which inputs should be focused on in characterizing input distributions for use in the Monte Carlo-based approach.
The results of the sensitivity analysis allowed the inputs to be ordered in terms of their impact on the intake term or SIF using the Monte Carlo methodology. The magnitude of the impact that an input had on the intake term or SIF was a function of both the inputs mathematical relationship to the SIF and the range identified for that input. The results of the sensitivity analysis were combined with an assessment of the quality of information available from the literature for characterizing each input. The final result of the sensitivity analysis was a list of those inputs that will receive special focus in characterizing distributions.
The next step in the Monte Carlo methodology was to generate continuous or discrete probability functions (PDFs) for all relevant inputs. In the Monte Carlo approach, each of many input variables can become a random variable with known or estimated PDF. Within this framework, a variable would take on a range of values with known probability. Some distributions, for instance, were based on known human variability and came into play in the analysis because of the uncertainty as to who will be involved in the scenario. Once the exposure models, variables, and constants for the models were defined, the next step was to use a suitable software to make a large number of realizations of the set of random variables in each model. For each realization, the computer drew one random value from the appropriate distribution for each of the random variables in the model and computed a single result. This computation was repeated a large number of times to produce complete distributions of modeled variables. Finally, the distributions were plotted and various statistical summaries of the results were produced to help interpret the data.
The final step in the development and evaluation of the Monte Carlo methodology was the generation of the SIF or intake distribution. The SIF generated using the EPA point estimate methodology then was compared to the distribution generated using the Monte Carlo approach. This comparison was useful in that the relative position of the point estimate on the probability density function provided a perspective as to the conservatism of the point estimate.
The computer software used in this Monte Carlo uncertainty analysis was Crystal Ball software program, which is an add-on to the Microsoft Excel spreadsheet program. The use of Crystal Ball software allows Excel spreadsheets to be incorporated directly into the Monte Carlo approach. The Crystal Ball program allows either Latin Hypercube Sampling or the default conventional sampling method usually used in Monte Carlo simulations. The default method generates random values for each distribution over the entire range defined for that distribution. This approach can accurately reflect the shape of distributions if enough iterations are completed in order to allow values in the more obscure tail regions of distributions to be sampled. The Latin Hypercube method divides distributions into regions of equal probability. Latin Hypercube Sampling was used in this evaluation to quickly stabilize the tail regions of the output distribution. This approach ensured that all regions of a distribution were sampled with equal frequency. Table K.5.1.1 provides a summary of the PDFs used in the Monte Carlo-based uncertainty analysis.
The number of iterations used in the Monte Carlo simulation was based on the work of Thompson (Thompson 1992). In this approach, a simulation is run twice, each time using 10,000 iterations. If the 95th percentiles from the resulting distributions differ by more than 1 percent from each other, the number of runs used in the simulation is increased until the differences between 95th percentile values falls below the arbitrary 1 percent mark. Runs of 10,000 iterations were found to produce stable risk distributions in this analysis.
Sections K.5.1.3 through K.5.1.9 provide the results of the Monte Carlo uncertainty analysis and sensitivity analysis as they pertain to the individual receptor of the specific exposure scenarios analyzed in the EIS. The uncertainties associated with the cumulative risk over 10,000 years for each exposure scenario are discussed in Section K.5.1.1.6.
K.5.1.3 Native American Scenario
The Native American scenario was intended to include a wide range of activities from traditional lifestyle activities ( i.e., hunting and fishing) to contemporary lifestyle activities (i.e., irrigated farming). Specific activities include hunting, gathering, collecting, fishing, and processing of the catch along the shoreline, and pasturing of livestock, as well as ceremonial, educational, seasonal, social, and trade activities. A detailed description of the Native American scenario is provided in DOE (DOE 1996).
The focus of this section of the report is to evaluate the uncertainty associated with the SIF as it pertains to exposure pathways specific to the Native American scenario. The SIFs evaluated for the Native American scenario were based on Tribal input because currently there are no standards or data regarding Tribal-specific intake factors. Therefore, the SIFs for the Native American scenario were compared against the ICRP recommendations (e.g., ICRP 1975) or EPA standards (e.g., EPA 1989) for humans. This could result in more uncertainty than for the other scenarios that were based on EPA standards. The exposure pathways that would contribute the greatest risk to a Native American include: groundwater ingestion, meat and fish ingestion, and the inhalation of volatile compounds (i.e., while in a sweat lodge). Please refer to Volume Three, Section D.2.1.3 for a complete discussion of the risk associated with each exposure pathway in the Native American scenario.
Table K.5.1.1 Summary of Probability Density Functions
Uncertainty in the Groundwater Ingestion Summary Intake Factor
The Native American scenario groundwater ingestion SIF was based on exposures over a 70-year duration to an individual residing onsite. The exposed individual was assumed to ingest 3 L (0.8 gal) of water a day 365 days a year (DOE 1996). The groundwater ingestion SIF is expressed by the following equation:
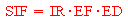
Where:
SIF = Summary intake factor (liters)
IR = Ingestion rate (liters/day)
EF = Exposure frequency (days/year)
ED = Exposure duration (years)
Substitution of the fixed point estimate for IR, EF, and ED resulted in a groundwater ingestion SIF of 7.67E+04 L (DOE 1996).
The U.S. Army and EPA historically have used 2 L/day (0.5 gal/day) as an average water consumption rate (EPA 1989). However, the scientific literature suggests an average drinking water consumption rate of 1.4 L/day (0.37 gal/day) (EPA 1989). Burmaster has shown that drinking water ingestion rates follow a lognormal distribution with a mean value of 1.12 L/day (0.30 gal/day) and a standard deviation of 1.63 L/day (0.430 gal/day) (Burmaster 1992). For purposes of this uncertainty analysis, the drinking water ingestion rate was approximated by a triangular distribution. The maximum value was assumed to be 3 L/day (0.8 gal/day) (DOE 1996); most likely value 2 L/day (0.5 gal/day) (EPA 1989); and minimum value 1.1 L/day (0.29 gal/day) (Rosenberry-Burmaster 1992).
The exposure duration and exposure frequency parameters for the Native American scenario were assumed to follow distributions similar to those of United States populations. The time spent at a residence followed a lognormal distribution with a mean value of 4.55 years and a standard deviation of 8.68 years (Israeli-Nelson 1992). The exposure frequency for ingestion of drinking water was approximated using a triangular distribution with a maximum of 365 days/year, most probable value of 345 days/year and a minimum of 180 days/year (Smith 1994).
Monte Carlo uncertainty and sensitivity analyses were performed on the groundwater ingestion SIF. The sensitivity analysis indicated that the parameters that contributed the most to the uncertainty in the groundwater ingestion SIF as measured by rank order were exposure duration, ingestion rate, and exposure frequency. The results of the Monte Carlo analysis are summarized in Table K.5.1.2.
Table K.5.1.2 Native American Scenario Groundwater Ingestion SIF Estimates 1
Table K.5.1.2 contrasts the mean and percentile estimates of the PDF for the groundwater ingestion SIF for the Native American scenario with the value derived using upper-bound fixed point estimates for IR, EF, and ED. The results show that the SIF derived using the upper-bound values lies above the 95th percentile of the SIF PDF. The mean of the SIF probability distribution was one order of magnitude lower than the fixed point estimate. This result suggests that the Native American scenario drinking water SIF derived using default parameters is an upper-bound estimate and may not be representative of the typical intake of a hypothetical future Native American resident.
Uncertainty in the Fish Ingestion Summary Intake Factor
The Native American scenario fish ingestion SIF was based on exposures over a 70-year duration to an individual residing onsite. The exposed individual was assumed to consume 1,080 g/day (2.4 lb/day) of fish for 365 days/year (DOE 1996). The fish ingestion SIF is expressed by the following equation:
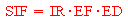
Where:
SIF = Summary intake factor (kg)
IR = Ingestion rate (kg/day)
EF = Exposure frequency (days/year)
ED = Exposure duration (years)
Substitution of the default estimates for IR, EF, and ED resulted in a fixed point estimate for the fish ingestion SIF of 2.76E+04 kg (6.1E+04 lb) (DOE 1996). Consumption rates for recreationally caught fish from large bodies of water have a 50th percentile average of 30 g/day (1 oz/day) and a 90th percentile average of 140 g/day (0.3 lb/day) (EPA 1989). Therefore, for purposes of this scenario, the fish ingestion PDF was approximated by a triangular distribution. The maximum value was assumed to be 1,080 g/day (2.4 lb/day) (DOE 1996); most likely value 140 g/day (0.3 lb/day) (EPA 1989); and minimum value 30 g/day (1 oz/day) (EPA 1989).
The time spent at a residence followed a lognormal distribution with a mean value of 4.55 years and a standard deviation of 8.68 years (Israeli-Nelson 1992). The exposure frequency for ingestion of fish was approximated using a triangular distribution with a maximum of 365 days/year, most probable value of 345 days/year and a minimum of 180 days/year (Smith 1994).
Monte Carlo uncertainty and sensitivity analyses were performed on the fish ingestion SIF. The sensitivity analysis indicated that the parameters that contributed the most to the uncertainty in the fish ingestion SIF as measured by rank order were exposure duration, ingestion rate, and exposure frequency. The results of the Monte Carlo analysis are summarized in Table K.5.1.3.
Table K.5.1.3 Native American Scenario Fish Ingestion SIF Estimates 1
Table K.5.1.3 contrasts the mean and percentile estimates of the SIF for the fish ingestion PDF for the Native American scenario with the fixed point estimate derived using the upper-bound values. The results show that the SIF derived using the upper-bound values lies above the 95th percentile of the SIF probability distribution. The mean of the SIF probability distribution was one order of magnitude lower than the fixed point estimate. This suggests that the Native American Scenario fish ingestion SIF derived using default parameters is an upper-bound estimate and may not be representative of the typical intake by a Native American resident.
Uncertainty in the Groundwater Volatile Organic Compound Inhalation Summary Intake Factor
The Native American scenario groundwater volatile organic compound (VOC) inhalation SIF was based on exposures over a 70-year duration to an individual residing onsite. The exposed individual was assumed to have an inhalation rate of 15 L/day (4 gal/day) 365 days/year (DOE 1996). The VOC inhalation SIF is expressed by the following equation:

Where:
SIF = Summary intake factor (liters)
IR = Inhalation rate (cubic meters/day)
EF = Exposure frequency (days/year)
ED = Exposure duration (years)
VF = Volatilization factor (liters/cubic meter)
The volatilization factor (VF) was used to approximate the quantity of water in indoor air based on the absolute humidity (Andelman 1990). This factor was used to account for activities such as showering, cooking, and time spent in a sweat lodge. The VF was assumed to be 0.1 for the purposes of this calculation (DOE 1996). The groundwater VOC inhalation SIF fixed point estimate using default parameters was 3.84E+04 L (1.01E+04 gal) (DOE 1996).
Indoor air inhalation rates have been shown to vary depending on the activity level of the exposed individual (Layton 1993). On average, inhalation rates for time spent indoors during showering have been shown to vary from a maximum value of 30 m3/hr (1,060 ft3/hr) to an average of 11 m3/hr (390 ft3/hr) to a minimum of 2 m3/hr (71 ft3/hr) (EPA 1989). For the purposes of this evaluation, a triangular distribution with these limits was used to describe the Native American scenario VOC inhalation SIF.
The exposure duration and exposure frequency parameters for the Native American scenario were assumed to follow distribution similar to those of populations in the rest of the United States. Israeli-Nelson (1992) showed that the time spent at a residence follows a lognormal distribution with a mean value of 4.55 years and a standard deviation of 8.68 years (Israeli-Nelson 1992). The exposure frequency for ingestion of drinking water was approximated using a triangular distribution with a maximum of 365 days/year, most probable value of 345 days/year, and a minimum of 180 days/year (Smith 1994).
Monte Carlo uncertainty and sensitivity analyses were performed on the groundwater VOC inhalation SIF. The sensitivity analysis indicated that the parameters that contributed the most to the uncertainty in the SIF as measured by rank order were exposure duration, inhalation rate, volatilization factor, and exposure frequency. The results of the Monte Carlo analysis are summarized in Table K.5.1.4.
Table K.5.1.4 Native American Scenario VOC Inhalation SIF Estimates 1
Table K.5.1.4 contrasts the mean and percentile estimates of the PDF for the groundwater VOC inhalation SIF for the Native American scenario with the fixed-point estimate derived by using the upper-bound values. The results indicated that the SIF derived using the upper-bound values lies at approximately the 95th percentile of the SIF probability distribution. Furthermore, the mean of the SIF probability distribution function was approximately one-third the magnitude of fixed-point estimate. This suggests that the groundwater VOC inhalation SIF derived using default parameters is an upper-bound estimate.
K.5.1.4 Residential Farmer Scenario
The residential farmer scenario was based on a 30-year exposure of an individual residing onsite. The individual was assumed to be exposed to contaminated soil, air, surface, and groundwater, and homegrown fruits and vegetables 365 days per year. The evaluation for the residential scenario indicated that the site risk to a resident was driven by the drinking water ingestion exposure pathway. The exposed individual was assumed to ingest 2 L (0.5 gal) of contaminated water per day, 365 days per year for 30 years. The drinking water ingestion SIF may be expressed by the following equation:
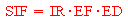
Where:
SIF = Summary intake factor (L)
IR = Ingestion rate (L/day)
EF = Exposure frequency (day/year)
ED = Exposure duration (year)
The point estimate for the SIF for ingestion of drinking water was 2.2E+04 L (5.8E+03 gal) (DOE 1995). Drinking water ingestion rates were shown by Burmaster to following a lognormal distribution with a mean value of 1.12 L/day (0.3 gal/day) and a standard deviation of 1.63 L/day (0.43 gal/day) (Rosenberry-Burmaster 1993). Similarly, the time spent at a residence follows a lognormal distribution with a mean value of 4.55 years and a standard deviation of 8.68 years (Israeli-Nelson 1992). The exposure frequency for ingestion of drinking water was approximated using a triangular distribution with a maximum value of 365 days/year, most probable value of 345 days/year and minimum value of 180 days/year (Smith 1994).
A Monte Carlo uncertainty and sensitivity analysis was performed on the SIF for drinking water ingestion. The results of the sensitivity analysis indicated that parameters that most influence the SIF for drinking water ingestion were in rank order: ingestion rate, exposure duration, and exposure frequency. The results of the Monte Carlo-based analysis are summarized in Table K.5.1.5.
Table K.5.1.5 contrasts the PDF percentile estimates of the SIF for groundwater ingestion for the residential farmer scenario with the point estimate derived using the EPA upper-bound values. The results show that the point estimate lies above the 95th percentile of the SIF probability distribution. The mean of the SIF probability distribution was approximately one order of magnitude lower than the EPA point estimate. This result demonstrates that the drinking water SIF derived using EPA default parameters is an upper-bound estimate and may not be representative of the typical intake of any hypothetical future resident.
Table K.5.1.5 Residential Farmer Scenario Drinking Water Ingestion SIF Estimates 1
K.5.1.5 Industrial Worker Scenario
The industrial exposure scenario was based on worker exposure over a 20-year duration. The scenario involved mainly indoor activities, although outdoor activities (e.g., soil contact) also were included. Latent cancer fatalities (LCFs) for this scenario were shown to result principally from the inhalation of radiological atmospheric emissions. The SIF for the inhalation exposure route may be expressed by the following equation:

Where:
SIF = Summary intake factor (m3)
IR = Inhalation rate (m3/day)
ED = Exposure duration (years)
EF = Exposure frequency (days/year)
The SIF using EPA default factors assumed that the air inhalation rate was 20 m3 per day for a worker and external exposure occurred for 8 hours per day. Inhalation of radionuclides occurs 250 days per year and external exposure would occur 146 days per year. The point estimate SIF for inhalation of radionuclides was 1.0E+05 m3 (3.5E+06 ft3) (DOE 1995).
A Monte Carlo uncertainty and sensitivity analysis was conducted using the above algorithm for calculating the industrial worker SIF. The results of the sensitivity analysis indicated that parameters that most influence the industrial worker SIF were in rank order: exposure duration, inhalation rate, and exposure frequency. The results of the Monte Carlo-based analysis are summarized in Table K.5.1.6.
Table K.5.1.6 Industrial Worker Scenario Inhalation SIF Estimates 1
Table K.5.1.6 contrasts the PDF percentile estimates of the air inhalation SIF distribution for the industrial worker scenario with the point estimate derived using the EPA upper-bound values. The results show that the point estimate is equal to the 95th percentile of the inhalation SIF probability distribution. The 50th percentile of the inhalation SIF probability distribution was one order of magnitude lower than the EPA point-estimate. This result demonstrates that the worker inhalation SIF derived using EPA default parameters is an upper bound estimate and may not be a realistic estimate of the true intake or exposure to an industrial worker at the Hanford Site.
K.5.1.6 Recreational Shoreline User and Recreational Land-User Scenarios
The recreational shoreline user scenario represented exposure to contamination in the Columbia River and shoreline from recreational swimming, boating, and other shoreline activities. The scenario involved mainly outdoor activities and would occur from exposure 14 days/year for 30 years.
The total adverse health impacts to a hypothetical future recreational shoreline user were expressed as the incremental lifetime cancer risk (ILCR) from the present to sometime in the future. The uncertainty associated with the adverse health effects predicted from this scenario can be attributed to the uncertainties in the source concentration, transport modeling, exposure parameters, and toxicological factors used to predict the total ILCR. However, the results of the risk analysis (Volume Three, Table D.5.1.2) indicated that the ILCR would be insignificant (i.e., less than 1E-10) for a period of 10,000 years. The uncertainties in the source concentration, and transport modeling would have to have had a combined uncertainty on the order of 1E+04 to 1E+06 to have a significant effect on the final result. This degree of conservatism is not likely to have been introduced into the final risk calculation.
The total adverse health impacts to a hypothetical future recreational land user scenario were expressed as total cancer incidence from the present to a time 10,000 years in the future. The uncertainties in the exposure factors alone have been shown for other scenarios (i.e., residential farmer) to be a least one order of magnitude too high when compared to the mean of the exposure term. Factoring this uncertainty into the final cancer risk predictions for the future recreational land user would result in mean cancer incidences at least one order of magnitude less than the predicted incidence rate. This conclusion seems justified given the fact that there was considerable uncertainty in the intermittent exposure terms used for this scenario.
K.5.1.7 Intruder Scenario
The potential consequences of intrusion into a Hanford Site solid waste burial ground at some time in the future were estimated by assuming a "post-drilling resident" scenario in which someone has a vegetable garden in the soil resulting from the drilling of a 30-cm (1-ft) diameter well. Furthermore, in order to represent the potential dose from all pathways via irrigation, a combination of farming and garden irrigation was used. In this scenario, a farm over the waste site was assumed to have 1 percent of the plant roots in the waste. One-fourth (25 percent) of the farmers vegetable intake and all (100 percent) of his meat and milk intake were assumed to be locally produced (i.e., contaminated). Furthermore, a well near the waste site was assumed to irrigate the vegetable garden. A more detailed description of the intruder scenario is presented in Volume Three, Section D.7.0. and in Rittman (Rittman 1994).
The results of the dose estimates for the intruder scenario (Rittman 1994) indicated that of the three principal routes of exposure (i.e., external, ingestion, and inhalation) the external would be the principal route of exposure followed by inhalation and ingestion. Thorium-232 (Th-232) was shown to be the radionuclide of concern (see Volume Three, Table D.7.3.1). The point estimate for the intruder scenario dose factor for Th-232 was 1.2E+04 mrem per year per curie exhumed. This point estimate was derived by assuming conservative upper-bound intake parameters. A Monte Carlo uncertainty and sensitivity analysis then was conducted on the algorithm used to calculate the intruder scenario effective dose factor (Rittman 1994). The sensitivity analysis indicated that parameters that contributed the most to the uncertainty in the intruder effective dose were in rank order: soil concentration, external exposure time, soil density, contamination depth, inhalation exposure time, and residential lot surface area. The results of the Monte Carlo analysis are summarized in Table K.5.1.7.
Table K.5.1.7 Intruder Scenario Dose Estimates 1
Table K.5.1.7 contrasts the PDF percentile estimates of the dose estimates for the intruder scenario with the point estimate derived using the upper-bound values. The point estimate lies at approximately the 100th percentile of the dose probability distribution function. The mean of the intruder dose probability distribution function was approximately an order of magnitude lower than the point estimate. These results demonstrated that the dose estimates predicted for the intruder scenario by using default EPA exposure factors were conservative and could be an unrealistic estimate of the effective dose received by a hypothetical intruder.
Source terms from intrusion were probabilistic. The probability and consequences associated with the intruder scenario would be as follows: the intruder scenario in the TWRS EIS is the same as the intruder scenario in the Disposal of Hanford Defense High-Level, Transuranic, and Tank Wastes Final EIS, Sections R.3 and R.5. Both are based on Aaberg and Kennedy (Aaberg-Kennedy 1990). The Disposal of Hanford Defense High-Level, Transuranic, and Tank Wastes Final EIS conducted a comprehensive probability and consequence analysis of radionuclide release and transport after disposal as a result of human intrusion. The results of this study were applied directly to the TWRS EIS intruder scenario uncertainty analysis.
The existing estimated risk to the intruder was based on the consequences only. The basic advantage of a probabilistic approach is that the probabilities of events occurring and the consequences are both taken into account. This gives a broader perspective of the performance assessment than a consequence analysis alone.
The amount of waste exhumed was estimated for each aggregated area. Estimates of annual probabilities for drilling into a tank or capsule are given in Table K.5.1.8. Source terms (initial exhumed inventory) were estimated for each drilling for each alternative (Volume Three, Tables D.7.1.1 to D.7.1.6). The following equation was used for calculating the yth percentile value of the accumulated release of constituent n from waste class w to the land surface due to drilling:
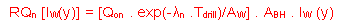
Where:
RQn = initial inventory (Ci) of radionuclide n in waste class w
Tdrill = time of drilling (year) after the year 1995 (100
years)
AW = surface area of waste class w (km2)
ABH = surface area of borehole (7.0E-08 km2)
IW(y) = the yth percentile value of the number of
boreholes in waste class w
The term  in the previous equation is the
exhumed inventory as presented in Volume Three, Tables D.7.1.1 to D.7.1.6.
Therefore, the yth percentile value of the exhumed waste for each
radionuclide and each alternative can be calculated as:
in the previous equation is the
exhumed inventory as presented in Volume Three, Tables D.7.1.1 to D.7.1.6.
Therefore, the yth percentile value of the exhumed waste for each
radionuclide and each alternative can be calculated as:
RQn [IW(y)] = Iexhumed . IW(y)
The percentile values for each class of waste are presented in Table K.5.1.9. These values were estimated using the Poisson distribution.
Table K.5.1.8 Annual Probabilities of Drilling into the Waste and Waste Surface Area
Table K.5.1.9 Percentile Values of Number of Boreholes in Each Waste Class (in a 10,000-year period)
Secondary sources of uncertainty are the transport and accumulation of radionuclides in the food chain, exposure pathways, and dose conversion factors. The exposure pathway parameters are the most easily quantified of these sources. The expected ranges and selected values for the exposure pathway parameters for drilling and post drilling are shown in Table K.5.1.10.
K.5.1.8 Total Health Impacts for Post-Remediation Land Users
The total adverse health impacts to a hypothetical future land user were expressed as the total calculated cancer fatalities over a 10,000-year period. The cancer fatalities were calculated by first computing the total cancer risk for a given population then dividing by the dose to risk conversion factor for cancer incidence and cancer fatalities (ICRP 1991). As shown in Volume Three, Section D.5.14.1, the total cancer fatalities for a given time span may be computed by the following equation:
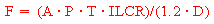
Table K.5.1.10 Selected Parameter for Intruder Scenario
Where:
F = Total cancer fatalities (persons)
A = Area corresponding to ILCR (km2)
P = Population density (persons/km2)
D = Duration of each generation (years)
T = Time span (thousand years)
ILCR = Incremental cancer risk for a given area
1.2 = Dose to risk conversion factor for cancer incidence and cancer
fatalities
The total cancer fatalities for a given time span may be computed as shown in the example problem of Volume Three, Section D.5.14.1. Using the previous equation and the sample problem of Section D.5.14.1, the point estimate for total cancer fatalities (F) may be computed as follows:
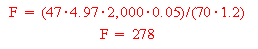
The uncertainty associated with the total cancer fatalities to a post-remediation residential farmer may be estimated using the Monte Carlo approach. The previous equation assumed that both population density (P) and duration of each generation (D) were fixed values when in fact there would be considerable uncertainty associated with each of these parameters. The Monte Carlo approach assumed that population density (P) would be a triangular distribution with a maximum value of 5 persons per km2, most probable value of 3 persons per km2, and a minimum value of 1 person per km2. The expected life span of a generation was represented as a lognormal distribution with mean of 75 years and standard deviation of 7.5 years (EPA 1989). The results of the Monte Carlo analysis are summarized in Table K.5.1.11.
Table K.5.1.11 Post-Remediation Land Users Fatality Estimates 1
Table K.5.1.11 contrasts the percentile estimates of the post-remediation land users fatality estimates with the point estimate value derived using the EPA upper-bound values. The total fatalities derived using the upper-bound values were greater than the 95th percentile of the fatality probability distribution. The mean of the fatality probability distribution was approximately 56 percent of the point estimate.
A note of qualification is appropriate with regard to the long-term, post-remediation collective doses and risks presented in the EIS. The National Council on Radiation Protection (NCRP) (NCRP 1995) cautions that the application of the concept of collective dose as a means of estimating prospective risks to populations from potential radiation exposures is subject to practical limitations. A calculated collective dose may contain such large inherent uncertainties that it would be a poor indicator of risk and therefore should not be considered as a basis for decision. The NCRP notes that neither population size and characteristics nor environmental exposure pathways for most radioactive elements are predictable with any degree of confidence for more than a few generations into the future (NCRP 1995). The NCRP also cautions that the summation of trivial average risks over very large populations or time periods into a single value may produce a distorted image of risk that is completely out of perspective with risks accepted every day, both voluntarily and involuntarily. In many instances, the collective dose increases with increasing size of the exposed population, but the benefits and risks to individuals remain nearly constant. Population exposure pathways and other assumptions have been projected for this EIS out of 10,000 years using the best available data and considered judgment but clearly are subject to the considerable uncertainty suggested by the NCRP. Therefore, the collective dose projections presented in the EIS should not be considered an exact measure of the true (absolute) quantity of dose or risk for any alternative. However, they are useful for comparison of the relative risk of the alternatives because the parameters that contribute large uncertainties are constant across the alternatives.
Finally, the NCRP suggests that whenever the collective dose is smaller than the reciprocal of the relevant risk coefficient, the risk assessment should note that the most likely number of consequences (e.g., cancer deaths) is zero. For example, the most likely ILCR for a cumulative population dose of 1,000 person-rem would be zero because the reciprocal of the relevant risk factor of 5E-04 (i.e.,1/5E-04 = 2,000).
K.5.1.9 Total Health Impacts Along the Columbia River
This scenario was used to estimate the dose to a population of people exposed to contamination from the Columbia River. The contamination would enter the Columbia River as a result of groundwater flow into the river. Different contaminants would enter the groundwater and reach the Columbia River at varying times in the future. Transport of contaminants through the groundwater is described in detail in Volume Four, Appendix F.
Total cancer fatalities were calculated using factors that relate the number of fatal cancers to the curies of each contaminant released to the river. These factors were calculated using a computer program that estimated the time integral of collective dose over a period of up to 10,000 years for time variant radionuclide release to surface waters, such as rivers (DOE 1987). The results of the dose estimates for the Columbia River scenario indicated that of the three principal routes of exposure (i.e., external, ingestion, and inhalation), ingestion would be the principal route, followed by inhalation and external exposure. The Np-237 was shown to be the radionuclide of concern to hypothetical receptors along the Columbia River (Rittman 1994). The point estimate for the Columbia River scenario dose equivalent factor for Np-237 is 1.0E+04 person-rem. A Monte Carlo uncertainty and sensitivity analysis was conducted on the algorithm used to estimate the dose for the Columbia River scenario. The sensitivity analysis indicated that parameters that most influenced the equivalent dose were in order: root uptake factor, root ingestion rate, Columbia River flow rate, total population exposed, months per year of irrigation, and soil area density. The results of the Monte Carlo analysis are summarized in Table K.5.1.12.
Table K.5.1.12 contrasts the percentile estimates of the dose estimates for a hypothetical Columbia River receptor with the point estimate derived using the upper-bound values. The point estimate lies at approximately the 100th percentile of the probability distribution function. The mean of the Columbia River probability distribution was approximately one order of magnitude less than that of the point estimate. Again, these results suggested that the dose estimates predicted for the Columbia River scenario were upper-bound estimates. The typical dose to a receptor could be an order of magnitude less than that predicted by the fixed-point estimate.
Table K.5.1.12 Columbia River Scenario Dose Estimates 1
K.5.2 REMEDIATION ROUTINE EXPOSURE
The range of possible unit dose factors for offsite receptors would primarily depend on individual consumption rates and environmental transport factors such as the soil-to-plant concentration ratio. Age-dependent variations were considered to have less effect because the generally higher internal dose factors for the lower age groups (ICRP 1975) were offset by the lower breathing and food consumption rates. Thus, age dependence was not expected to be as important as the factors mentioned.
To analyze the bounding range for the individual consumption rates, the standard maximum individual in GENII was considered to have the highest likely consumption rate. The lower end was taken to be the consumption rates used in recent low-level waste performance assessments at the Hanford Site (Kincaid et al. 1995; Wood et al. 1995). These were 25 percent of the average annual dietary intakes of garden produce and 50 percent of the average annual dietary intakes of meat, poultry, milk, and eggs. In the calculation of population dose, this variation disappeared in the population average consumption rates. Thus, for estimating the range of possible population unit dose factors, the only contributor was assumed to be the variation in agricultural transfer factors.
To analyze the bounding range for the various agricultural transfer factors, the values found in NUREG/CR-5512 (Kennedy-Strenge 1992) were used with scale factors. For the soil-to-plant concentration ratios, the scale factors were selected to be 0.1 and 10 to accommodate the large variation in the published values. The variation of the equilibrium transfer factors into animal products was taken to be 0.3 and 3, because there is more consistency in the reported values. To account for the smaller variation over population averages, these variations were reduced by a factor of 2. The food consumption rates (kg/year) from EPA and GENII are listed in Table K.5.2.1.
Scenario dose factors were computed using GENII Version 1.485 (Napier et al. 1988) with two exposure scenarios. The first was the air pathway chronic dose for the MEI at the site boundary. The normalized integrated exposure (Chi/Q) was set equal to 1 and unit activities of each nuclide of interest were used. The second exposure scenario was for the total population, again with a unit Chi/Q. The dose results are shown in Table K.5.2.2.
Table K.5.2.1 Food Consumption Rates (kg/year) for 25 Percent of EPA and for GENII
Table K.5.2.2 Dose Factor for the Offsite MEI and Population Using Best Estimates
Table K.5.2.2 compares the effect of changing food transfer factors from those currently in GENII to those in NUREG/CR-5512. The most significant change occurs for Tc-99, which would contribute little to the overall air pathway dose. Thus, for the TWRS comparisons, the two sets of food transfer factors can be considered the same.
Table K.5.2.3 shows the dose factors that resulted when the low consumption rates were combined with the low transfer factors, as well as when the high consumption rates were combined with the high transfer factors. The unit release dose factors for the offsite maximally-exposed individual (MEI) differed only in these two assumptions. The exposure times, average breathing rate, and other agricultural parameters were held constant.
Using the dose factors listed in Tables K.5.2.2 and K.5.2.3, the estimated dose factor range were reduced to a ratio of the low or high value divided by the expected value using the NUREG/CR-5512 transfer factors. These ratios are shown in Table K.5.2.4.
Table K.5.2.4 Ratios of Bounding 1 and Expected 2 Dose Factor
The above ratios could not be used to determine the bounding range of doses for mixtures of nuclides unless one nuclide gives nearly all the dose. For other cases, the doses must be computed for the mixture and then the bounding ratios can be calculated from the total dose. An example is given in Table K.5.2.5. From this table, the MEI dose factor ranged from 0.1 to 2.3 times the reported dose, while the offsite population dose ranged from 0.7 to 1.3 times the reported dose. These ratios were calculated by dividing the low or high dose value for each receptor by the best dose estimate.
These results show small uncertainties in the estimated dose calculations. The overall uncertainties associated with airborne transport, accumulation of constituents in food products, and dose conversion factors were not as significant as the source and release terms.
Table K.5.2.5 Comparison of Routine Dose Calculation for Mixtures of Nuclides
K.5.3 REMEDIATION ACCIDENTAL EXPOSURE
Radiological exposure to the receptor groups was based on the radiological activity concentrations in the source term. Activity concentrations for six composite inventories were used as the radiological source terms in the tank farms accident analyses. The bounding composite inventory bounds 100 percent of all the tank characterization sample data. The nominal inventory was a total tank farm average by volume based on the inventory of radioactive materials contained in the fuel from the single-pass reactors and N Reactor and transferred to the tank farms. GENII was used to generate a single unit liter dose (ULD) value for each composite source term. The bounding ULDs for the six composite inventories and the nominal ULD used in the accident analyses are presented in Table K.5.3.1. The greatest difference between bounding and nominal is the Aging Waste Facility (AWF) solids inventory with a ratio of 6.00E+02.
Table K.5.3.1 Accident Source Term Unit Liter Dose Values for Bounding and Nominal Scenarios
In Volume Four, Section E.15, analysis is presented regarding uncertainties associated with the accident analysis for the tank waste alternatives. For the operation accidents, uncertainties were associated with the inventory of waste in the tanks and the atmospheric conditions that would transport the waste released as a result of an accident. The tank waste inventory used in this EIS is presented in Volume Two, Appendix A along with uncertainties associated with the quality of the data. Because of this uncertainty, for tank farm accidents, a composite inventory was developed. This composite incorporated estimates of the historical tank contents, the results from prior individual tank analyses, and the results of recent tank characterization programs (Shire et al. 1995). This composite provided a bounding tank waste inventory for the accident analysis.
Atmospheric conditions would influence the dispersion of contaminants in air to potential receptors. The bounding case analyzed in the EIS used conservative atmospheric conditions (99.5th percentile). The uncertainty analysis compared the results of these bounding case conditions to typical atmospheric conditions (50th percentile).
There also were uncertainties associated with the analysis of consequences of an accident involving the transportation of vitrified HLW to the potential geologic repository under certain tank waste alternatives. The potential consequences would be influenced by the weight percent of HLW that would be mixed in the glass. The baseline analysis in the EIS assumed a 20 percent waste loading. However, waste loading could be as low as 15 percent or as high as 40 percent. Uncertainties associated with waste loading are discussed further in Volume Two, Section B.8. To address this uncertainty in Volume Four, Section E.15, the impacts of a transportation accident involving the baseline waste loading were compared to an accident involving vitrified glass with a 15 percent waste loading and with a 40 percent waste loading. In addition to the uncertainties associated with the accident analysis, a number of important assumptions influenced the results. These assumptions include the following:
- The offsite general public population for operation accidents was based on 1990 census data. While it is unlikely that the population would be constant throughout the operation phase of each alternative, the 1990 census provided a uniform basis for comparison of impacts among the alternatives.
- The onsite worker population for operation accidents was based on the 1995 Hanford Site work force. In the future, the Site work force would likely decline, resulting in proportionately lower impacts than presented in the EIS. However, use of the existing worker population provided a bounding analysis in terms of total impacts and provided a basis for uniform comparison of impacts among the alternatives.
- For transportation of HLW to a potential geologic repository, the accident scenarios were based on transportation of the waste from the Hanford Site to Yucca Mountain, Nevada by rail.
- For nonradiological occupational construction, operation, and transportation accidents, it was assumed that injuries, illnesses, and fatalities would occur at rates similar to historical rates for each activity.
- It was assumed that there would be no evacuation of Hanford Site personnel in the event of an accident. Emergency planning and evacuation programs are in place at the Hanford Site to mitigate potential consequences resulting from an accident.
The uncertainties in calculating the radiological doses and the toxicological exposures resulting from operation accidents included the tank inventory concentration and the atmospheric dispersion once the source term is in the air. A sample accident scenario is presented in Table K.5.3.2 to illustrate these uncertainties. The illustration shows the difference between the bounding and nominal parameters; the concentration of the inventory was a factor of 30; and the atmospheric dispersion coefficient was a factor of 12 for the MEI noninvolved worker, 30 for the noninvolved worker population, 22 for the MEI general public, and 15 for the general public population. For the noninvolved worker population, a bounding dose of 2.52E+03 person-rem was estimated. This was 3 orders of magnitude higher than the estimated nominal dose of 2.89E+00 person-rem.
The main uncertainty associated with estimating the radiological doses resulting from accidents while transporting vitrified HLW to a potential geologic repository was the weight percent of the waste that could be mixed with the glass matrix. A sample accident scenario is presented in Table K.5.3.3 to illustrate these uncertainties. The baseline analysis used in the EIS assumed a 20 percent loading. A range from 15 to 40 weight percent was used in the uncertainty evaluation in Table K.5.3.3. The population dose was calculated by RADTRAN 4 (Neuhauser-Kanipe 1992) and was based on the worst credible accident parameters in the urban population zone.
The accident initiator frequencies were established using currently accepted sources such as natural phenomena statistics for the Hanford Site or recent analysis of the initiators from safety assessment reports. The frequencies of these accidents were presented as estimates and were provided as an aid in screening accident scenarios. Only 10-fold differences in frequencies would be significant. For example, accident frequencies of 1E-6 and 5E-05 should not be considered significantly different.
The nonradiological injuries and fatalities resulting from construction and operation accidents were based on incidence rates in the occupational injuries summary report (DOE 1994j). The transportation injuries and fatalities from trucks and trains were based on incidence rates in statistics compiled by the U.S. Department of Transportation (Rao et al. 1982). Injuries and fatalities resulting from employee vehicle accidents were based on incidence rates in the Washington State Highway Accident Report (WSDT 1993). Because these are widely accepted, statistically based incidence rates, there was no attempt to evaluate the uncertainties.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|




