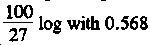Chapter 6
Nuclear Defense
Nuclear operations present unique challenges to commanders, unit NBC defense teams, and chemical staff personnel. To provide the required accurate information and battlefield intelligence, numerous mathematical calculations must be performed. These calculations are used to--
This chapter details the mathematical procedures required to provide this essential information.
Optimum Time of Exit for Fallout Areas
Radiological fallout may present a serious hazard to units that remain in a contaminated area. Shelters, such as field emplacements, are the best protective measures against nuclear radiation for troops. If the shelter provides any appreciable amount of protection, it will be advantageous to remain and improve the shelter rather than to evacuate to an uncontaminated area. If the situation permits, and higher headquarters approves, the commander may decide to move out of the contaminated area. By evacuating at the optimum exit time, the radiation dose to personnel is kept to a minimum.
To compute the optimum exit time for a fallout area, you must know the time of detonation, location of uncontaminated area; and the average transmission factor of the vehicles used and the shelters involved, plus the time required to evacuate the position.
If the nuclear burst was not sighted by the unit, the nearest NBCC will provide the H-hour.
When moving from an area contaminated by fallout, the unit moves into an uncontaminated location. This will necessitate waiting until fallout is complete at present positions.
The average transmission factor of the fallout shelters and the vehicles used to leave the contaminated area must be computed. Since all shelters are not the same, an average value should be used. The transmission factor of a vehicle may be calculated. A unit moving on foot will be fully exposed and will have a transmission factor of 1.0.
The time to load vehicles and move out of the contaminated area must be estimated. To minimize exposure time, it may be necessary to temporarily abandon nonessential items and recover them at a later time when the dose rate has decreased to an acceptable value.
The following abbreviations are used in optimum time of exit calculations:
Topt = MF x Tev.
Topt = optimum time of exit.
MF = multiplication factor.
Tev = time (in hours) required to evacuate the contaminated area.
Ae = average transmission factor of the vehicles used during movement out of the contaminated areas.
As = average transmission factor of the shelter. (This includes vehicles being used as shelters).
Compute the optimum exit time using the three following steps:
Step 1. Calculate the transmission factor ratio, As/Ae.
Step 2. Determine the multiplication factor. Enter the vertical axis of Figure 6-1 with the value obtained for As/Ae. Move horizontally along this value to the curve. Move straight down and read the multiplication factor from the horizontal axis.
Step 3. Calculate the optimum exit time. Multiply the multiplication factor by the Tev. The product is the optimum time, in hours after detonation, that the unit should leave its shelters and evacuate the area. Optimum time of exit equals the multiplication factor times Tev.
Special Considerations
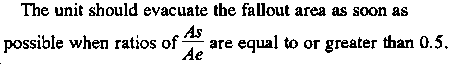
If the optimum time of exit is estimated to be before the actual arrival of fallout, the unit should evacuate the area as soon as possible after fallout is complete and an uncontamianted area is available.
The unit will receive the smallest dose possible if it leaves the contaminated area at the optimum time of exit. If the unit commander is willing to accept up to a ten percent increase in dose, he or she may leave the shelters any time between one-half and twice the optimum time of exit.
If possible, personnel should improve their shelters while waiting for the optimum time of exit. This, however, should only be attempted if the personnel do not have to leave the shelter to improve it. The estimate of the optimum time of exit should be recalculated if significant improvement is made in the shelters. Improved shelters mean the unit may remain for a longer period, to minimize the dose to personnel.
Sample Problem
Given: As = 0.1 (foxhole)
Ae = 0.6 (2½-ton truck)
Tev = 1 hour
Find: Optimum time of exit
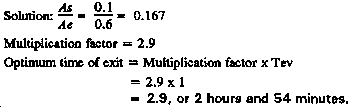
Optimum time of exit calculations bring up two other areas that are a vital part to radiological operations. One is transmission factors and the other is the calculation of H-hour.
Transmission Factors
A transmission factor (TF) is that fraction of the outside (ground) dose or dose rate received inside the enclosure that provides the shielding. (Refer to Appendix B for a more detailed discussion on shielding). TFs are always less than one. TFs are used to find the reduction in dose or dose rates received when personnel are protected from radiation.
TFs are always determined in operational situations by the unit NBC defense team. Each TF is calculated using the formula below:

Problem 1. The outside dose is 90 cGyph. Use the transmission factor to calculate the inside dose. What dose would troops in M113 armored personnel carriers receive? The TF for an M113 is 0.3.
|
ID |
= OD x TF |
|
= 90 x 0.3 |
|
|
= 27 cGy |
Problem 2. Transmission factors also may be applied to dose rates. A measured outside dose rate is 100 cGyph. The inside dose rate is calculated by use of the transmission factor. Find the dose rate inside the M113:
|
ID |
= OD x TF |
|
= 100 x 0.3 |
|
|
= 30 cGyph |
A list of precalculated transmission factors are in Table 6-1. These TFs are for the most exposed occupied location. They are not based on dose rates from fallout; they are based on gamma radiation from Cobalt 60. Energies from radioactive elements are measured in million electron volts (MEVs). The average from Cobalt 60 is roughly 1.25. Average energy from gamma activity in fallout is 0.67. Since Cobalt-60 radiation is almost twice as strong as the radiation from fallout, actual TFs should be much smaller (more protection).
Note that these TFs are not used under operational situations. Commanders and operations personnel use these precalculated TFs to judge the relative shielding ability of various vehicles and shelters. They are provided also for instruction and practice. For vehicles that have AN/VDR2s installed, each user need only verify that the correct attenuation factor has been entered (IAW TM 11-6665-251-10) and then read the outside dose directly off the display. The attenuation factor is the mathematical inverse of the transmission factor and has already been calcualted for many vehicles. These factors are printed on the mounting bracket for the AN/VDR2.
Another method that may be used to calculate the shielding properties is using a protection factor (PF). PF may be calculated with the following formula:

Calculation of H-Hour
H-hour may be calculated mathematically or by using the ABC-M1 radiac calculator. Calculate H-hour mathematically, using the following procedure (All calculations must be made after fallout is complete.):

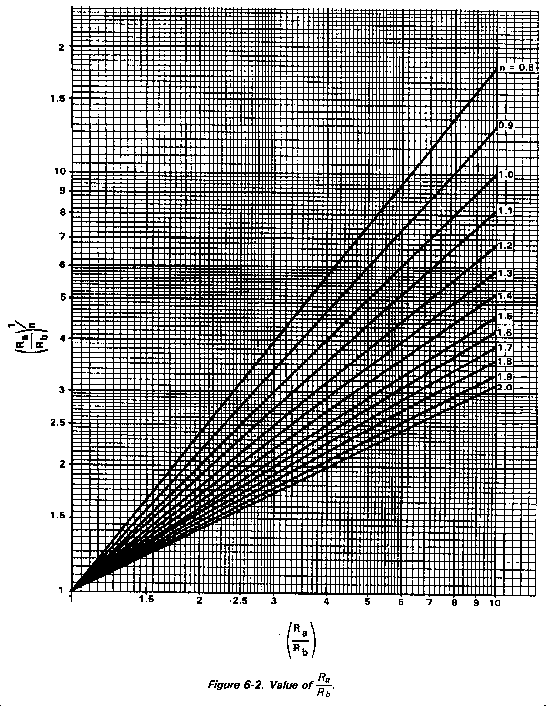
from a family of slopes (Figure 6-2). To calculate, use an assumed decay exponent or one that has been determined.
For example, monitoring reports Ra and Rb represent the earliest and latest data available for a particular location within a contaminated area:
Ra = 112 cGyph (0500, 15 January)
Rb = 24 cGyph (2200, 15 January).
From Figure 6-2, assuming n = 1.2
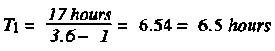
Since T1 is the time after H-hour at which reading Ra was made, the H-hour = Ta -T1 = 0500, 15 January - 6.5 hours = 2230, 14 January.
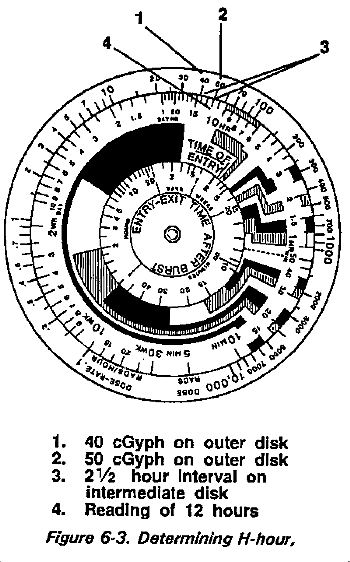
Use of ABC-M1 Radiac Calculator
The ABC-M1 radiac calculator (Figure 6-3) may be used to determine H-hour (if n = 1.2) as follows:
|
Time |
Dose Rate |
|
1600 |
50 cGyph |
|
1830 |
40 cGyph. |
As mentioned previously, the NBC 3 nuclear report is only a prediction which provides a means of locating probable radiation hazards. Militarily significant fallout will occur within the predicted area. However, the prediction does not indicate exactly where the fallout will occur or what the dose rate will be at a specific location. Where fallout will occur is a function of weather and terrain. The most significant weather effect, as far as fallout is concerned, is commonly referred to as rainout or washout.
Rainout and Washout
Rainout and washout are nothing more than the removal of radioactive particles from a nuclear cloud by precipitation when the nuclear cloud is below or within a percipitation cloud. Even when rain clouds are not present, rainout or washout may occur. This will depend on the amount of water evaporated by the fireball and rising as water vapor. Such evaporation may occur when a nuclear detonation occurs over a large body of water, such as a lake or ocean. A nuclear weapon detonated in a high humidity area may also result in rainout or washout. When water vapor rises with the nuclear cloud, it will cool and condensate in the atmosphere, then fall back to the surface as rain.
If the airborne radioactive debris from a nuclear burst should encounter precipitation, a large portion of the debris may be brought to earth with the rain or other moisture. The resulting fallout pattern will be irregular, producing local hot spots within the fallout pattern. Although an air burst normally does not produce any militarily significant fallout, precipitation in or above the nuclear cloud can cause significant contamination on the ground. Precipitation may also affect the fallout distribution from surface or sub-surface bursts by washing contamination from one location and depositing it in lower areas.
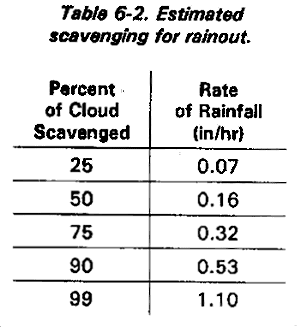
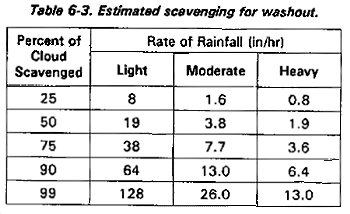
There are basically two factors that must be considered to determine whether or not rainout will occur and to what extent. The first is duration of the precipitation--the longer the precipitation the greater the percentage of the nuclear cloud will be washed or scavenged. Table 6-2 represents this percentage as a factor of precipitation duration. This occurs when a nuclear cloud is within a rain cloud. Notice, rainfall rate appears to have little effect on rainout. Washout, on the otherhand, occurs when the nuclear cloud is below the rain cloud. Here, the rainfall rata directly effects the amount of scavenging that will occur. Table 6-3 reflects this effect. The terms light, moderate, and heavy in this table refer to rates of 0.05, 0.2, and 0.47 inches of rain per hour, respectively, as measured at the surface. Thus, it would appear that rainout is more effective than washout in scavenging a nuclear cloud.
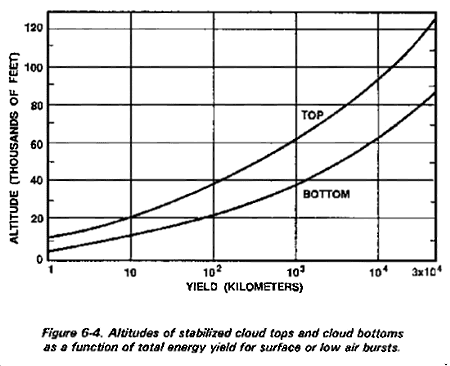
The other factor is the altitude of the stabilized nuclear cloud versus the altitude of the rain or snow cloud. The altitudes of most rain cloud tops range from 10,000 to 30,000 feet. The bottom of these clouds, where most precipitation emerges, is commonly at an altitude of about 2,000 feet. Precipitation from severe thunderstorms may originate as high as 60,000 feet. If the rain cloud is smaller than the nuclear cloud, then only that portion of the nuclear cloud covered by the rain cloud will be affected by washout or rainout; whichever applies. If the nuclear cloud extends past, or higher than the top of the rain cloud, then only that portion of the nuclear cloud that lies within and under the rain cloud will be affected. Figure 6-4 depicts the average heights or altitudes of stabilized nuclear cloud tops and bottoms, per yield for surface and low-air bursts. Obtain data from the staff weather service to determine the heights of clouds that cover the area in which the nuclear burst occurred. This will provide data that can be used to determine whether or not the nuclear cloud will be subject to washout or rainout.
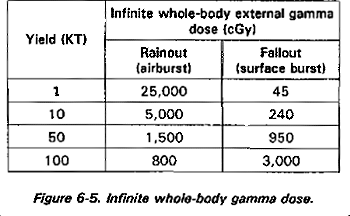
If the nuclear cloud should drift into a rain or snow cloud at some point after the burst, the surface contamination caused by scavenging will be decreased due to radioactive decay. The longer between detonation and entering into the rain cloud, the less radioactive material will be present. Finally, the particles that are scavenged will not be deposited on the ground immediately, but will fall with the precipitation (typically 800 to 1,200 feet per minute for rain and 200 feet per minute for snow). Since the particles are scavenged over time and over a range of altitudes, horizontal movement during the fall of particles will tend to decrease the concentration of radioactivity on the ground. This movement and deposition will result in elongated surface fallout patterns. The exact shape will depend on the amount of rainfall, wind, and surface conditions. However, the radioactivity deposited on the ground from rainout is much more significant than that of dry or normal fallout. This is due primarily to the fact that rainout causes the radioactive particles suspended in the atmosphere to fall to the surface at a faster and more concentrated level than dry fallout. Research of this phenomena was conducted in the early 1970's and yielded the data presented in Figure 6-5. This data suggests that the contamination from low yield air bursts subject to rainout produces radioactive contamination at a much more significant level than dry fallout from a surface burst. This is due primarily to the rain or snow forcing the particles of fallout to the ground faster and in a heavier concentration.
Tactical Implications
Exposed personnel without access to structures, vehicles or field works offering a reasonable radiological protection factor (such as, trenches with 18 inches of earth overhead cover) would soon become non-effective if they were in an area of rainout from a lower-yield weapon(s). The area would be contaminated to such an extent as to render it dangerous for them to remain in the affected area long without receiving an incapacitating dose of radiation.
Runoff from the affected area, containing high-intensity radiological contamination, could contaminate water supplies in an adjacent unaffected area. Runoff in contaminated areas will flow into water sources such as lakes, rivers, and streams, creating concentrated energy levels. Monitor water sources with the AN/PDR27 set on the higher scale and the probe in a plastic bag, before consuming or entering the water.
It seems obvious that certain extra warning measures should be implemented. Divisional NBCCs should give special warnings to units that may be subject to rainout. At present it is not yet practicable to give this with great accuracy, but enough should be known to enable sensible forecasts to be made. Guidance, based on this forecast may then be passed to affected units on what action commanders should be prepared to take. One obvious action is that they should order continuous monitoring when rainout is forecasted or at the onset of rain. If rainout occurs, they are faced with one of two simple choices: either get their units under proper cover, or get them away from the area--if tactical considerations permit. It is worth mentioning that the enemy is unlikely to occupy the vacated area for the same reason the unit leaves it.
Period of Validity and Decay Rate
Fallout will decay according to the following Kaufman equation--
R1T1n = R2T2n.
R = dose rates at a single location, and 1 and 2 correspond to the times they were taken.
T = time in hours after H-hour, that readings 1 and 2 were taken.
n = decay exponent, and 1 and 2 denote different times after H-hour. When 1 denotes H + 1, and 2 denotes any other time, the equation becomes R2 = R1 T2 -n.
Dose calculations and pattern evaluations depend upon decay rate. So the decay exponent must be known. In fallout contamination, the value of n will not necessarily be constant with time or even constant throughout a particular contaminated area, although the pattern as a whole will have an average value. This average value will vary from pattern to pattern.
|
Caution When dealing with overlapping contamination patterns, using an average n value for the overall pattern can lead to serious error. |
The amount of variation is expected to be from about 0.2 to 2.0 for fallout. The lower values of n also can be expected for salted weapons. Salted weapons refers to weapons that have additives included in the warhead generally to produce or increase induced radiation. The average value of n for most patterns (referred to as standard decay) will be 1.2. Standard decay may be assumed when decay-rate determination has not yet been made.
Determination of decay rate depends on H-hour. A sequence of dose-rate readings (NBC 4 nuclear Series reports) from several selected locations is required. The reliability of the decay-rate calculation depends on the precision of the dose-rate readings, the interval over which the readings are taken, and the time over which dose calculations are to be made. That is, the more reliable the dose-rate monitoring and the longer the time interval over which they are taken, the longer the time in which reliable dose calculations can be made.
As a rule of thumb, reliable dose calculations can be projected in time (Tp-period of validity) over a period three times as long as the monitoring time interval. The period of validity (Tp) is a mathematical calculation that determines how long the decay rate is good. For example, for a decay rate determined from monitoring readings taken between H + 4 and H + 8, dose calculations could be reliably projected from H + 8 to H + 20 (TP = H + 8 + [3 (8 -4)] = H + 20). Additional monitoring data will extend this time. Thus, the calculations based upon decay rate are valid for 20 hours after the burst. The date-time representing 20 hours from the attack is recorded on the contamination overlay as the do-not-use-after date-time group. This calculation is placed on the contamination overlay to advise the user of the length of time the calculations are valid.
The formula for determining the period of validity Tp is--
Tp = 3 ( Tb - Ta) + Tb
An illustration of the preferred method in which decay-rate determinations and estimations are used in developing a contamination pattern is presented below. Additional methods to calculate the decay rate are presented in Appendix F.
Example: Collection effort for a fallout-producing nuclear burst (H-hour known) begins at H + 4. It is expected to be completed by H + 6. The target time for preparation of the pattern is H + 8. By H + 6, a decay estimation can be made and the remainder of the dose-rate information processed. This will result in a reasonably reliable H + 1 pattern. By H + 6, a decay-rate determination can be accomplished to allow the use of the pattern until about H + 12. By H + 12, a decay-rate determination can be made to allow use of the pattern until H + 36 hours. Each extension of time extends the do-not-use-after date-time group for the contamination plot.
Determination of Decay Rate
Determine the decay exponent by solving the Kaufman equation for n:
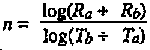
Ra = dose rate (cGyph) measured at time, Ta (a peak dose rate recorded at H + 1 or later).
Rb = dose rate (cGyph) measured at time, Tb (the last dose rate available).
Ta = the time (H + _ hours after burst) that dose rate Ra was measured.
Tb = the time (H + _ hours after burst) that dose rate Rb was measured.
n = decay rate of fallout.
Note: Ra, Rb, Ta, and Tb are determined from the NBC 4 nuclear series reports submitted by units that have been directed by the NBCC to pass dose rate readings every half hour for 2 hours, followed by hourly reports. These reports begin after the NBC 4 peak has been determined.
Table 6-4 provides nontypical logarithms of numbers. The tables consist of two columns
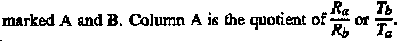
The logarithm of that quotient is found in Column B.
Note that Column A is given to one decimal place only. To use the table, round your quotient to the nearest single decimal place, and locate that number in Column A. Read the logarithm of that number in Column B.
Example: 10 divided by 6 equals 1.666666667. Round to 1.7, and enter Column A with 1.7. The logarithm from Column B is 0.230.
Sometimes, when using the logarithms in Table 6-4, you may need the log of a number that is not listed. In this case, mathematical estimation is required.
Example: You need the logarithm of 12.85. Reading down Column A in Table 6-4, you find values only for 12.8 and 12.9--none for 12.85. To find the log of 12.85--
Set the problem up like this and follow the four steps shown:
|
Value from Column A |
Value from Column B |
|
12.81.107 |
(log of 12.8) |
|
12.8 X |
(log of 12.85) |
|
12.91.110 |
(log of 12.9) |
Step 1. Take the difference between 12.8 and 12.85, which is 0.05. Take the difference between 12.8 and 12.9, which is 0.1. Set these values up as a numerator and

Step 2. Take the difference between 1.107 (log value of 12.8 derived from Column B, Table 6-4) and the log value of 12.85, which at this point, is unknown. This unknown is presented by an "x." Take the difference between 1.107 (log value of 12.8 derived from Column B in Table 6-4) and 1.110 (log value of 12.9 derived from Column B, Table 6-4. In this case, the answer is 0.003. Set these two
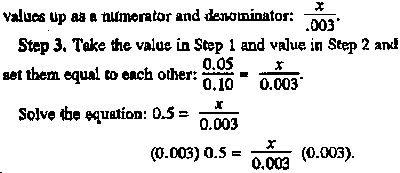
Step 4. Add the value of "x" (0.0015) to the log value of 12.8 (1.107). The answer will be the log value of 12.85.
1.107 (log value of 12.8)
+ 0.0015
1.1085 (log value of 12.85)
Normalizing Readings to H + 1
Once the decay rate (n) is determined, the radiological reading may be normalized to H + 1 readings. This normalized reading is commonly referred to as the R1 reading. It is nothing more than determining, mathematically what the dose rate reading was at any given location, one hour after the burst. Survey teams and monitors enter an area and take readings at various times after the burst (H-hour). These readings may be 15 minutes or 10 hours after the burst. Any reading that is not recorded 1 hour (H + 1) after a burst is commonly referred to as an Rt reading. To perform radiological calculations and make decisions on the nuclear battlefield, all readings must be represented using the same time reference. If this is not done, the radioactive elements will decay and a true representation of the hazard, past and present (because radioactivity is accumulative in the human body) cannot be made.
In other words--
First Situation--Monitor A reports a dose rate of 100 cGyph 5 hours after the burst. The decay rate is unknown, so the monitor assumes standard decay (n = 1.2). What was the dose rate at Monitor A's location at H + 1?
This can be determined by two methods; the nomogram method, which is the preferred method, but subject to operator error, and the mathematical method which is outlined in Appendix F.
The nomogram method uses the nomograms in Appendix E for the specific decay rate involved. The mathematical method requires a hand-held pocket calculator that has a power function, which is represented by a button labeled either "yx " or "xy."
Visualize the problem by preparing a situation matrix as follows:
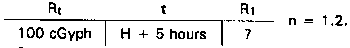
Step 1. Write the situation matrix (at left) to properly record the information in the problem.
Step 2. Find the nomogram for fallout decay using a decay rate (n) of 1.2 (see Figure E-16).
Step 3. Lineup a hairline on the value of 100 cGyph on the far left hand Rt column. Lay the hairline across 5 in the center Time column.
Step 4. Holding the hairline straight and steady, read the value in the right-hand R column. Your answer should be approximately 650 cGyph.
Second Situation--Further monitoring determines the decay rate to be 0.9. Monitor A's reading, using the procedure of the first situation, is normalized to a new R1 (H + 1) of 426 cGyph. The commander wants to know what the reading will be at Monitor A's location at H + 8 hours.
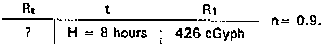
Step 1. Write the situation matrix (left) to properly record the information in the problem.
Step 2. Find the nomogram for fallout decay using a decay rate (n) of 0.9 (see Figure E-14).
Step 3. Line up the hairline on the value of 426 cGyph on the far right-hand R1 column. Lay the hairline across 8 in the center Time column. If the correct value is not listed (as in this problem for the number 8 in the Time column), approximate where the number would lie between 5 and 10.
Step 4. Holding the hairline straight and steady, read the value in the far left-hand Rt column. This answer should be approximately 65 cGyph.
Use the nomograms in Appendix E to solve similar problems. Be sure to select the correct nomogram for the stated decay rate.
Normalizing Factor
The NF corrects dose rate readings to the selected reference time. Readings from radiological surveys received from units must be normalized to H + 1 for use in plotting fallout contamination. The H + 1 calculations also are needed to estimate total dose. Normalizing factors may be found by using any of three methods: a table of values, mathematical, or graphical. The table of values method is the preferred method. The mathematical and graphical methods are discussed in Appendix F. Tables 6-5 and 6-6 are examples of tables of normalizing factors for selected times after a nuclear burst and for anticipated decay exponents. The reference time in Table 6-5 is H + 1. The reference time in Table 6-6 is H + 48 hours. This type of table normally is used when H-hour is known and the collection is initiated immediately. The following steps outline the procedure for using a table of values.
Step 1. Determine the time in hours and minutes after the burst that the reading was taken.
Step 2. Enter Table 6-5 with the time after burst. Read across to the appropriate decay exponent column and find the NF.
Step 3. Multiply the dose-rate reading by the normalization factor. The product is the H + 1 dose-rate reading.
The following example uses the table of values to determine the normalization factor, and uses it to convert R2 to R1.
Example:
The outside dose rate at 1 hour and 20 minutes after the burst was 100 cGyph. Enter Table 6-5 with 1 hour and 20 minutes and extract the normalizing factor of 1.41 from the 1.2 decay exponent column. (Because decay was not stated, assume standard decay of 1.2.) Calculate R1 as follows:
R1 = NF x R2
R1 = 1.41 x100 cGyph
R1 = 141 cGyph.
Total Dose Procedures
The dose rate of radiation does not directly determine whether or not personnel become casualties. Casualties depend on total dose received. If the dose rate were constant, total dose would simply be the product of the dose rate and the time spent in the contaminated area (just as in a road movement problem, Rate x Time = Distance). But the dose rate continually diminishes because of decay. This makes the calculation more complicated. The actual dose received is always less than the product of dose rate at time of entry times duration of stay.
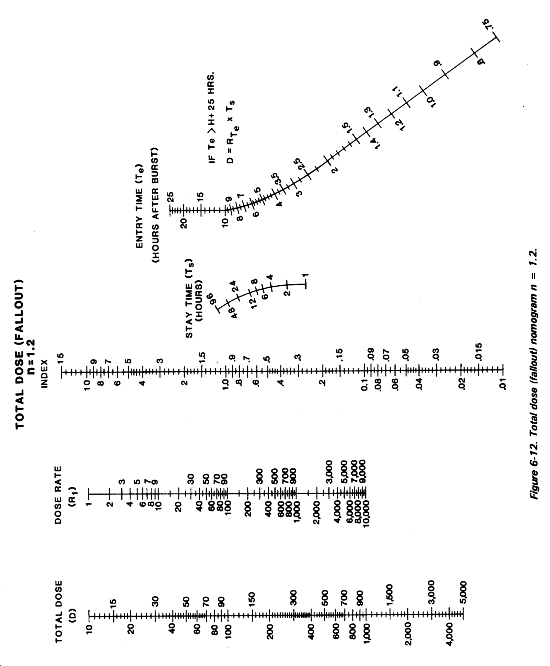
Total dose, time of entry, and time of stay calculations in fallout areas are solved in total dose nomograms. These nomograms are based on anticipated decay rates of n = 0.2 to n = 2.0 and are in Appendix E.
Total dose nomograms relate total dose, H + 1 dose rate, stay time, and entry time. The index scale is a pivoting line. It is used as an intermediate step between D and R1, and Ts and Te. The index scale value can be used to multiply the R1 to find the D. The four values on these nomograms are defined below:
R1 must be known before the total dose nomograms can be used. If any two of the other three values are known, the nomograms can be used to find the missing piece of information. Determination of R1 was discussed earlier.
D and R1, and Ts and Te are used together. When working with total dose nomograms, start the problem on the side of the nomogram where the two known values are located. If D and R1 are given, start on the left side. If Ts and Te are given, start on the right side. Never begin a problem by joining D or R1 with either of the time values.
The following problems are for single explosions only. Multiple-burst fallout procedures are covered later in this chapter.
Problem 1.
Given:
R1 = 200 cGyph
Te = H + 1.5 hours
Ts = 1 hour
n = 1.2.
Find: D.
Visualize the problem as follows:
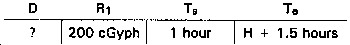
Answer: 90 cGy.
Solution.
Select the n = 1.2 total dose nomogram. Connect H + 1.5 hours on the Te scale and 1 hour on the Ts scale with a hairline. Pivot the hairline at its point of intersection with the index scle to the 200 cGyph on the R1 scale. Read D = 90 cGyph on the total dose scale.
Problem 2.
Given:
D = 20 cGy
R1 = 100 cGyph
Ts = 1 hour
n = 0.8
Find: Te
Visualize the problem as follows:
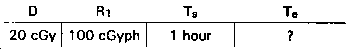
Answer: H + 6.6 hours.
Solution: Select the n = 0.8 total dose nomogram. Connect 20 cGyph on the D scale and 100 cGyph on the R1 scale. Pivot the hairline at its point of intersection with the index to the 1 hour on the Ts scale. Read Te = 6.6 hours on the Te scale.
Problem 3.
D = 50 cGy
R1 = 200 cGyph
Te = H+ 3 hours
n = 1.6
Find: Ts.
Visualize the problem as follows:
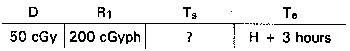
Solution: Select the n = 1.6 total dose nomogram. Connect 50 cGyph on the D scale and 200 cGyph on the R1 scale. Pivot the hairline at its point of intersection with the index scale to the 3 hour point on the Te scale. Read 2 hours on the Ts scale.
Problem 4. (Special case--Hairline off scale)
Given: R1 = 10 cGyph
Ts = 2 hour
Te = H+ 2 hours
n = 1.4.
Find: D
Answer: 4.6 cGy.
Visualize the problem as follows:
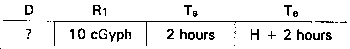
Solution:
Select the n = 1.4 total dose nomogram. Connect 2 hours on the Te scale and 2 hours on the Ts scale with a hairline. Pivot the hairline at its point of intersection with the index scale to 10 cGyph on the R1 scale. Note that the hairline crosses above the D column. To find D, multiply the value found where the hairline crosses the index scale by the R1. In this case, index = 0.46, and R1 = 10 cGyph. Therefore, D = 4.6 cGy.
By 25 hours after the burst, the change in the rate of decay is so low that it is relatively insignificant. Therefore, a different approach is used to estimate total dose when Te is greater than 25 hours. In this case, simply multiply the dose rate at the time of entry by the time of stay. This is written--
D = Rte x Ts.
D = total dose (cGy)
Rte = dose rate (cGyph) at time of entry
Ts = time of stay (hr).
For example--
|
Given: |
R1 |
= 300 cGyph |
|
Ts |
= 2 hours |
|
|
Te |
= H + 30 hours |
|
|
n |
= 0.9 |
Find: D
Answer: 28 cGy.
Visualize the problem as follows:
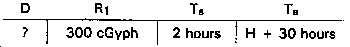
Solution: Select the 0.9 decay rate nomogram. Align 2 hours on the Ts scale with 30 hours on the Te scale. However, in this case there is not a 30 hour scale on the time of entry chart. Use the 0.9 fallout decay nomogram to determine what the dose would beat H + 30 hours.
Find dose:
D = Rte x Ts
D = 14 cGyph x 2 hr
D = 28 cGy
When Ts must be calculated against a dose limit or OEG, the above formula must be rearranged:

Now determine when (time) 300 cGyph will reduce to 14 cGyph. Align the R1 value and the Rt value. Note that the hairline crosses the time (t) scale at H + 30 hours.
Sometimes monitors or survey team members will record radiological contamination readings that are not normal readings. This situation may not be apparent until the readings are plotted by the NBCC on the situation map. These readings may record dose rates that are higher than what would be normal for that area. This difference may be caused by--rainout, which was discussed earlier, overlapping fallout from multiple bursts, and neutron-induced radiation.
Multiple Burst Procedures
Under nuclear warfare conditions, there probably will be occasions when a fallout prediction overlaps an area in which contamination already exists. Similarly, there may be cases in which fallout predictions overlap each other. For example, two fallout-producing bursts can occur within a few hours of each other--one upwind from the other.
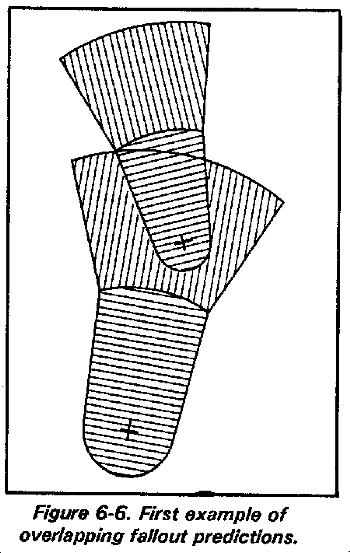
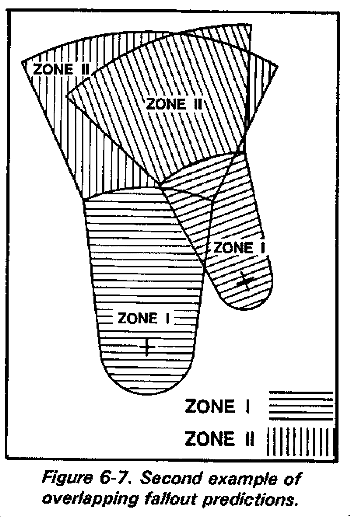
Use the following rule for determining the relative hazard when two or more fallout predictions overlap--The hazard classification of an area where predicted fallout hazard zones overlap should be only that of the higher classification involved. That is, an overlap area involving Zone I should be designated Zone I, and an overlap area involving nothing more hazardous than Zone II should be designated Zone II (see Figures 6-6 and 6-7).
The above rule is useful only for a matter of several hours after the bursts. The extent of contamination should be determined as soon as possible from monitoring and survey reports. When bursts are separated by several hours, the pattern already on the ground must be considered with the fallout prediction for the later burst.
It is highly probable that there will be areas on the battlefield subject to fallout from more than one nuclear weapon detonation. Procedures for predicting future dose rates in areas contaminated by single explosions are not adequate in many instances within overlapping fallout patterns. Fallout produced by more than one explosion normally has different decay exponents at different locations in the area. The next section outlines procedures for predicting future dose rates within overlapping fallout patterns.
Dose Rate Calculation Methods
The methods described next apply to two or more overlapping fallout patterns. The choice of method depends on whether the dose rates of each burst can be separated. If enough information is not available to separate the bursts or dose rates, refer to Appendix F.
If enough information is known to separate the different dose rates, use the following three steps:
Step 1. Separate the dose rates. You need the H-hour of each burst and two or more dose rate readings for the location of interest. Take these readings after the fallout from each burst peaks and prior to the arrival of new fallout. Use normal procedures for calculating the decay exponent (n) for each burst at the location of interest.
Step 2. Calculate separately the dose rate for the desired future time for each burst. Add the results. This procedure lets you calculate the total dose rate for a specific location at any time in the future.
Step 3. Repeat steps 1 and 2 for each location of interest within the overlapping fallout patterns.
If enough information is not known to separate the different dose rates, use the following procedures:
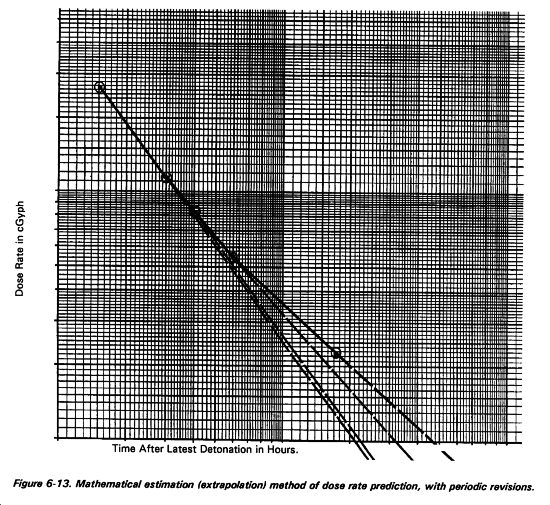
Step 1. For a specific location, use log-log graph paper and plot the last two dose rate measurements (after peak) against the time after the latest burst. (If the time of the latest detonation is unknown, estimate H-hour as the time of the latest known burst.)
Step 2. Draw a straight line through these points and extend the line to later times.
Step 3. Determine a first approximation of the future dose rate directly from the graph.
Step 4. Plot a later dose-rate measurement at that location when it becomes available.
Step 5. Draw a straight line through the new latest two points and extrapolate the line to later times.
Step 6. Determine a better approximation of the future dose rate directly from the latest extrapolation.
Step 7. Repeat steps 4, 5, and 6 as later dose rate measurements at that location become available.
Step 8. Repeat steps 1 through 7 for each location of interest within the overlapping fallout patterns.
Example of dose rate calculation:
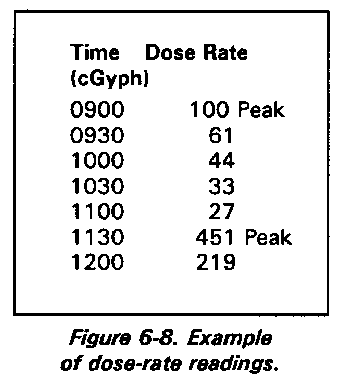
Problem: Fallout has been received from two detonations--one at 0800Z and one at 1100Z (see Figure 6-8).
Predict the dose rates for 0800Z at this location 24 hours after the burst. Sufficient data is available to separate the two bursts.
Solution: Separate the two dose rates. This can be done by two different methods: the logarithm method, which is preferred, and the calculator method found in Appendix F.
Logarithm chart method
R1a = Dose rate of first burst at H + 1.
R2b = Dose rate at the time of the second burst.
T2b = Time in hours after the first burst of the R2b reading.
T1a = Time (in hours after first burst) of the R1a reading.
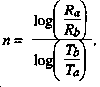
Step 1. Divide 100 by 27 to get 3.7. Turn to Table 6-4 for the logarithm chart. Read down Column A until you find 3.7. Read across to Column B, and extract the log of 3.7, which is 0.568.
|
Step 2. Replace |
|
in the formula. |
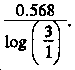
|
Step 3. Repeat Step 1 for log |
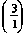 . . |
Once you divide 3 by 1, you should get 3. Turn to Table 6-4, and read down Column A until you
| find 3; read across to Column B, and read 0.477. Substitute this number for log |
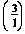 |
in the formula, just as in Step 2.
Step 4. The new formula should now look like this:
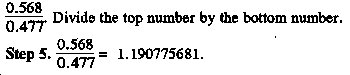
Rounding this number up to the nearest tenth (0.1), your answer should be an n value (or decay rate) of 1.2, which equals standard decay.
Step 6. Next, determine the decay rate for the second burst (see Figure 6-8). The second burst occurred at 1100. This is three hours after the first burst. The fallout from the second burst peaked prior to H + 1 (1200). Thus, the reference dose rate for this portion is 219 cGyph. Determine how much of this reading (219 cGyph) was contributed by the first burst. We know that the first burst occurred at 0800. This is four hours prior to our second burst's H + 1 value. Our H + 1 or R1 value for the first burst was 100 cGyph. Enter the nomogram for fallout decay of 1.2 found in Figure 6-9 with the R1 value of 100 and H + 4. Read the Rt value of 19 cGyph. Therefore, 19 cGyph of the 219 cGyph reading at 1200 was contributed by the first burst. Subtract 19 cGyph from 219 cGyph to determine the H + 1 value of the second burst. The formula to determine the decay rate of the second burst would look like this:
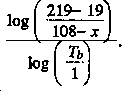
Step 7. The last reading in the report was 108 cGyph at 1300 This is five hours after detonation of the first burst. Using the same procedures outlined in Step 6, determine that 14.5 cGyph of the 108 cGyph reading was contributed by the first burst. Substitute the "x" value in our formula with 14.5 and substitute the Tb value for 2, since 1300 is 2 hours after the second burst. Our formula now looks like this:
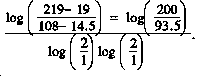
Step 8. Divide 200 by 93.5. This should equal 2.13. Enter the logarithm chart in Table 6-4 and read down Column A until you find 2.1. Due to the rules of simple rounding, you would go to 2.1. If this is not desired, you may mathematically estimate the log for 2.13. Extract the number 0.322. Divide 2 by 1 and enter the logarithm chart, find 2 and read 0.301. Divide 0.322 by 0.301. This gives you a decay rate for the second burst of 1.069 or 1.1:
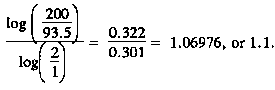
The nomogram method may now be used to calculate the dose rate at the time of operational interest.
Using a nomogram, calculate the 0800Z dose rate 24 hours after the first burst by finding the dose rate for that specific time for each burst separately, and add the two values. Use a decay rate of 1.2 for the first burst, and 1.1 for the second:
(n = 1.2 nomogram in Figure 6-9).
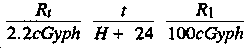
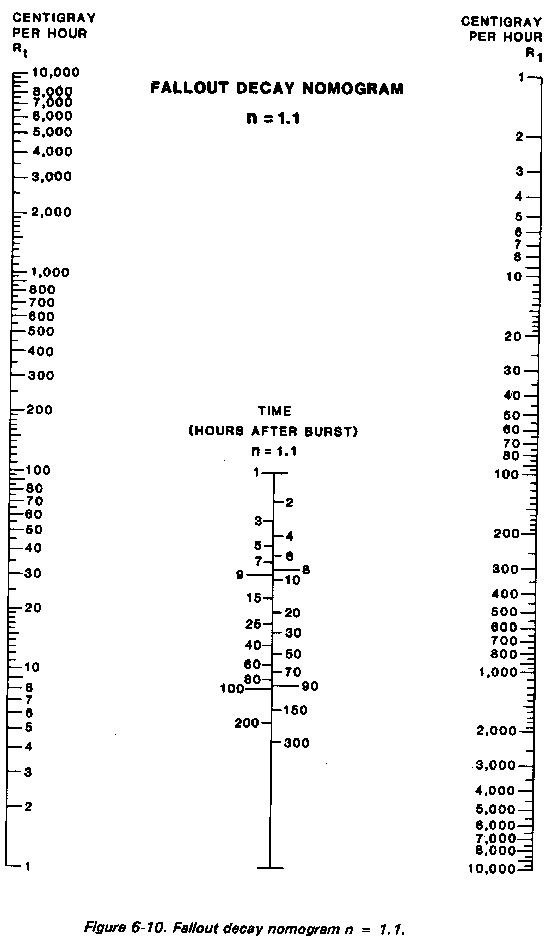
(n = 1.1 nomogram in Figure 6-10).
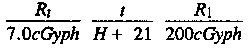
Dose rate total at 24 hours after the first burst is calculated as follows:
2.2 cGyph + 7.0 cGyph = 9.2, or 9 cGyph.
Dose Rate Calculations for Overlapping Fallout
H-hour is known for each burst. At 251500, a 20-KT nuclear weapon was detonated on the surface. Sometime later, fallout arrived on your position. At 1630, a peak dose rate of 126 cGyph was measured, Subsequent readings indicated that n = 1.4. At 251700, another weapon was detonated, and fallout arrived at ypur position soon after. At 251830, a second peak dose rate of 300 cGyph was measured.
Note: This problem also may be calculated with a hand-held pocket calculator. These procedures are outlined in Appendix F. The calculator procedures must be followed if the value for t (time) is less than 1 hour.
Problem 1. Assuming that n = 1.2 for the second weapon, what will the dose rate be at 2000? This may be calculated by either of two methods for determining an R1 value. The first method (A) is to follow the steps for using the nomogram. The second method (B) is outlined in Appendix F.
Solution:
When H-hour for each detonation is known, calculate the dose or dose rate for each event, and add them together to get the total dose or dose rate received.
Find R1 for the first detonation.
Visualize the problem as follows:

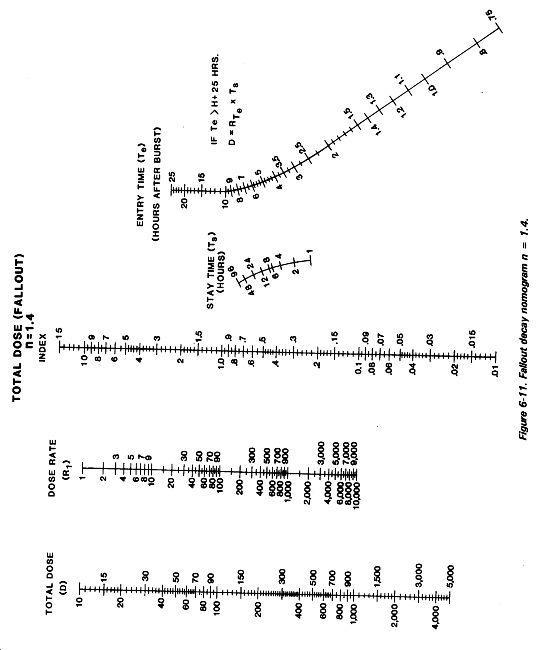
Step 1. Using the nomogram in Figure 6-11 for a decay rate of 1.4, line up the hairline across the Rt value and t value. Read 222 cGyph on the R1 scale.
Find Rt at 1830 hours for the first fallout only.
Visualize the problem as follows:
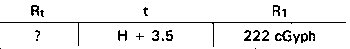
Step 2. Using the same nomogram as in Step 1, lineup the hairline across the R1 value of 222 and the t value of 3.5 (1830 is 3.5 hours after the first burst). Read the value of 38 on the Rt scale.
Step 3. Find the dose rate contribution at 1830 from the second burst. Subtract the Rt value determined in Step 2 from the reported dose rate at 1830 (300 cGyph). Dose rate contribution of the second burst is 262 cGyph.
Rt2 = Rt - R1
Rt = 300 cGyph - 38 cGyph
Rt = 262 cGyph
Step 4. Find R1 for the second burst only. Follow the procedures outlined in Step 1 to determine the R1 value. Use the 1.2 nomogram in Figure 6-9. Line up the Rt value of 262 cGyph and the t value of 1.5. Read the R1 value of 400 cGyph.
Find Rt at 2000 hour for each burst.
Visualize the problem as follows:
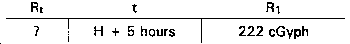
Step 5. For first burst, using the same nomogram as in Step 1, lineup the hairline on the R1 scale at approximately the 222 cGyph value. Hairline must cross the t scale at 5 (H + 5). Read the approximate value of 34 cGyph on the Rt scale.
R1 = 222 cGyph
t = H + 4 hours
For the second burst, using the 1.2 decay-rate nomogram as in Step 4, line up the hairline on the R1 value of 400 cGyph and cross the t scale at 3 (H + 3). Read the Rt value of 85 cGyph.
Step 6. Find the total dose rate at 2000 hours. Total dose rate is the sum of dose rates at that time. Add the Rt value of 34 cGyph at H + 5 for the first burst and the Rt value of 85 cGyph at H + 3 for the second burst.
total dose at 2000 = Rtl + Rt2
total dose at 2000 = 34 cGyph and 85 cGyph
total dose at 2000 = 119 cGyph
Problem 2. If a new unit moves into your area at 2200 and occupies foxholes for three hours, what total dose can they expect to receive? To work this portion of the problem, use the total dose nomogram for the decay rate of 1.4 in Figure 6-11.
Step 1. Find dose received from first burst. Visualize the problem as follows:
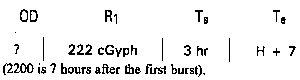
Note: In computing this problem do not consider any radiation exposure the unit may receive prior to entering the foxholes. For the purposes of this example, only consider the radiation exposure the unit will receive once it (the unit) enters the foxholes.
From Figure 6-11, read the value of 30 cGy. Multiply this value by the transmission factor for foxholes (0.1), found in Table 6-1.
ID = OD X TF
ID = 30 cGy x 0.1
ID = 3 cGy
Step 2. Find dose received from the second burst. Visualize the problem as follows:
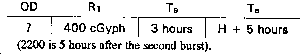
Using the nomogram for total dose, decay rate 1.2 in Figure 6-12, compute the following:
OD = 125 cGy
ID = OD X TF
ID = 125 cGy x 0.1
ID = 12.5 cGy.
Step 3. Find the total dose from both bursts.
D total = D1 + D2
= 3 cGy + 12.5 cGy
= 15.5 cGy.
Note: These values apply only to the location where the dose rate measurement was taken. The procedure must be repeated for each additional location.
Problem 3. You have the following information and monitoring data:
100900 H-hour
101030 350 cGyph (peak)
101100 260 cGyph
101200 163 cGyph
101400 94 cGyph, H-hour, second burst
101500 100 cGyph
101600 515 cGyph
101700 295 cGyph
101800 216 cGyph
101900 163 cGyph
Find the dose rate at 111100.
Solution:
Since H-hour is known for both detonations, a mathematical procedure can be used.
Step 1. Determine the decay constant for the first burst.
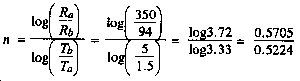
Answer: n = 1.09 = 1.1
Step 2. Using n = 1.1, calculate the contribution the first burst made to the total dose rate after 101500. Using the data presented in the problem and the decay value of 1.1, normalize the peak reading of 350 cGyph at H + 1.5 hours to H + 1. Using Figure 6-10 and the methods discussed previously, determine an H + 1 value of 530 cGyph.
Dose Rate from First Burst:
101000 (H + 1) 530 cGyph
101500 (H + 6) 78 cGyph
101600 (H + 7) 65 cGyph
101700 (H + 8) 55 cGyph
101800 (H + 9) 48 cGyph
101900 (H + 10) 43 cGyph
Step 3. Calculate the decay constant for the second burst.
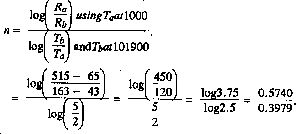
Answer: n = 1.444 = 1.4
Step 4. Calculate dose rate at 111100 for each burst, and add together.
Visualize the problem for the first burst (n = 1.1) as follows:
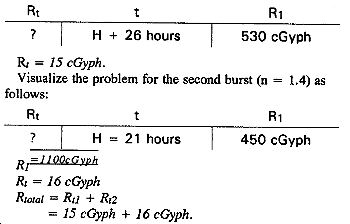
Answer: Rtotal = 31 cGyph.
H-hour is known only for the most recent burst. In this circumstance, a graphical approximation must be made.
Situation: There have been several surface bursts which have deposited fallout on your position. H-hour for the most recent detonation was 150700 hours. Monitoring reports since are listed below:
150700 30 cGyph
150800 128 cGyph
150830263 cGyph (peak)
151000 112 cGyph
Problem: Find the dose rate at 161000 using these steps:
Step 1. On log-log graph paper, plot the peak dose (263 cGyph) and subsequent dose rates. Draw a straight line through them extending to 161000 (H + 27 hours) (see Figure 6-13).
Step 2. Read as first extrapolation, 7.5 cGyph.
Situation (continued): It is now 151300 and you have received these additional reports:
15110083 cGyph
15130055 cGyph.
What is the projected H + 27 dose rate at this time?
Step 3. Plot the new data and connect the two most current values with a straight line, extending it to H + 27 hours.
Step 4. Read as a second extrapolation, 11.8 cGyph.
Situation (continued): It is now 152400, and the latest monitor report is 22 cGyph.
What is the projected H + 27 rate now?
Step 5. Plot the new data and connect the last two values with a straight line extending to H + 27 hours.
Step 6. Read as a third extrapolation, 15.5 cGyph.
Crossing a Fallout Area
In nuclear warfare, it is possible that extensive areas will be contaminated with residual activity. It may be necessary to cross an area where there is residual radiation. This might occur when exploiting our own nuclear bursts or in retrograde or offensive operations coupled with enemy-delivered nuclear bursts. These areas may be occupied eventually, but operations will be complicated because the total dose received by our troops must be kept to a minimum.
When crossing a contaminated area, the dose rate will increase as the center of the area is approached and will decrease as the far side is approached. Therefore, determine an average dose rate for total dose calculations. A reasonable approximation of the average dose rate can be determined by using one-half of the highest dose rate. This is written--
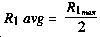
R1 average = average dose rate at H + 1
R1 max = highest dose rate encountered or expected to be encountered at H + 1.
After the average dose rate has been determined, entry times that will keep the total dose below that specified in operational exposure guidance can be computed on the basis of estimated stay times. Total dose also can be computed for specified entry times and stay times. The following paragraphs outline procedures for these calculations.
In calculating the total dose to be received when crossing a fallout area, you need the time of entry into the area, the average dose rate along the route, and the time of stay within the area. Use the total dose nomograms in Appendix E for these calculations.
In crossing, the average dose rate is equal to one-half of the maximum dose rate encountered on the route. If the maximum dose rate encountered is 60 cGyph, then--
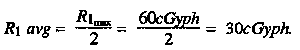
In crossing a fallout area, the length of exposure or time of stay must be calculated. The length of the crossing route within the outer perimeter of the contamination is divided by the average speed of crossing. This speed must be constant.

If the distance across an area is 2 kilometers, and the speed is a constant 20 kilometers per hour then--
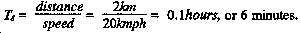
When a unit must cross a contaminated area, it is given OEG. (See Appendix A for more details on OEG.) This is the maximum permissible dose. The unit calculates various entry times and stay times that will keep the total dose below the OEG. The average dose rate also must be known. Transmission factors for vehicles are applied to total dose or dose rates. (Refer to Table 6-1.)
The following problems concern techniques only. They do not consider the impact that these doses or dose rates might have on operations in a contaminated area. When solving for total dose (D) with an actual stay time (Ts) of less than 1 hour, aline the hairline with 1 hour on the appropriate nomogram to obtain a total dose. Multiply this total dose figure by the actual decimal fraction of the time of stay to obtain the true total dose.
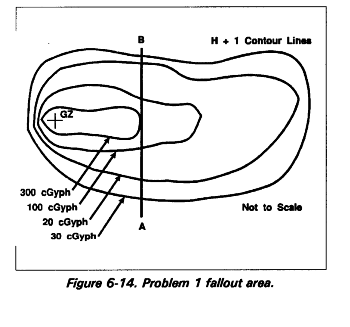
Problem 1.
Troops are to cross the fallout area in Figure 6-14 at H + 3 hours in M113s moving at 10 kmph. The route from A to B, a distance of 5 km, will be used. (Assume standard decay of 1.2).
Find: Total dose the troops will receive.
Visualize the problem as follows:
Answer: 9.6 cGy
Solution: Calculate the average dose rate as follows:
Te = H + 3 hrs
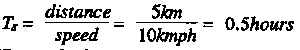
|
R1 |
= (highest exposure anticipated) |
|
= (300 cGyph) |
|
|
= 150 cGyph |
|
|
D |
= ? |
Use Figure E-36 to compute average dose rate.
D = 32 cGyph outside dose from nomogram at 1 hour Ts
D = 32 x .5) Ts)
D = 16 cGyph.
Calculate the inside dose:
TF = 0.3 (Table 6-1)
ID = OD x TF
= 16 x 0.3
= 4.8 cGy.
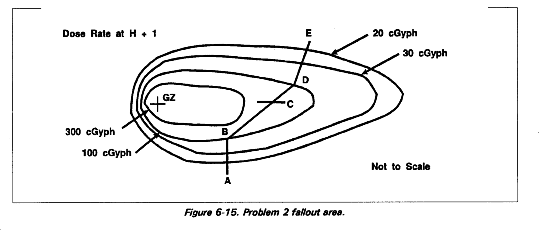
Problem 2.
Troops are to cross the fallout area in Figure 6-15 at H + 3 hours in 2-ton trucks moving at 15 kmph, using the route A-B-C-D-E. Total distance equals 7.5 kilometers.
Find: Total dose the troops will receive.
Answer: 7.2 cGy.
Solution:
1. Calculate the average dose rate:
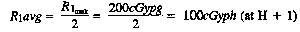
(Rl max at point C interpolated from Figure 6-16).
2. Calculate the time of stay:
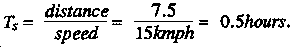
3. Find the outside dose:
R1 avg = 100 cGyph
Te = H + 3 hours
Ts = 0.5 hour
D = 12 cGy.
4. Calculate the inside dose:
TF = 0.6 (Table 6-1)
ID = OD x TF
= 12 x 0.6
= 7.2 cGy.
Problem 3.
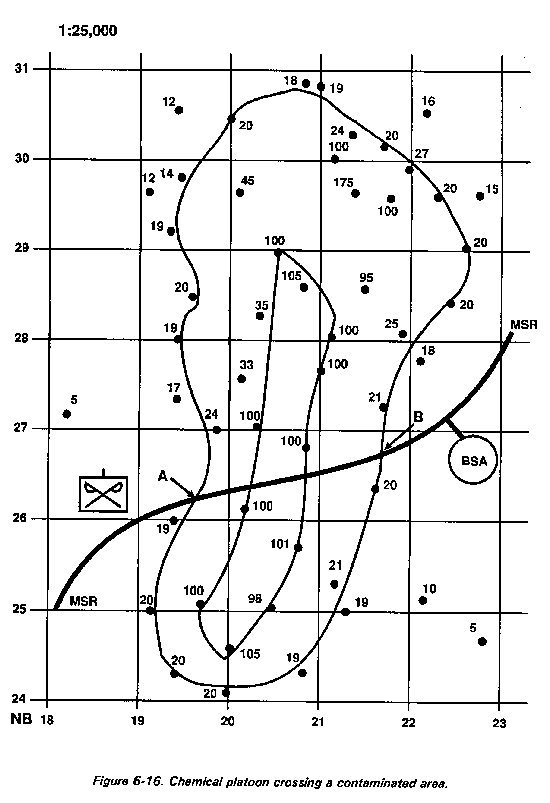
A chemical company smoke generator platoon operating within 1st Brigade's sector must top off its fog oil load while moving to the new mission site at the BSA (refer to Figure 6-16). A mountain range 3 kilometers, to the south and enemy activity 3 kilometers to the north prevent the platoon from maneuvering around the contamination. Time to complete this mission is essential. It is now 261830, and the platoon must have smoke on target by 262100 to support the next phase of 1st Brigade's operation. The platoon must move along the main supply route (MSR) to the brigade support area (BSA) to obtain more fog oil. Due to previous operations, the platoon is rated at RES 1 (moderate risk--as explained in Appendix A) and the soldiers are not to exceed 70 cGy total in this movement. The brigade S3 has turned to you, as the chemical staff specialist for 1st Brigade, and asked whether or not the platoon can accomplish this mission and not exceed the 70 cGy OEG. The S3 also wants to know what dose the platoon is expected to receive, and if there are any special precautions the platoon should take to limit its exposure.
Although presented as an example, this may be a typical situation on a nuclear battlefield, and is representative of what is commonly referred to as a crossing problem. The platoon will depart (SP) from its location (NB187262) at 1900 and travel in HMMWVs along the MSR at a speed of 25 kilometers per hour. Using the map scale in Figure E-1, Appendix E, answer the brigade S3's questions.
Step 1. Place a pencil compass on the center of the platoons position and measure over the 20 cGyph contour line where this contour line crosses the MSR. Without changing the compass gap, place the compass on the map scale in Figure E-1, Appendix E. Use the 1: 25,000 scale. The distance from the platoon's position to the 20 cGyph contour line should be 0.6 kms.
Step 2. If the platoon departs from its locaton at 1900, and travels 0.6 kms at 25 kmph, at what time will the platoon enter the contaminated area? To determine this use the following formula:
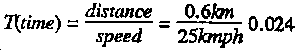
In other words, with a nuclear burst that occurred at 1500, the unit will depart at H + 4 hours. The distance that the unit must travel down the MSR, before it reaches the contaminated environment will take approximately 1.45 minutes. This is derived by multiplying 0.024 by 60 to gain the time in minutes. When working with radiological contamination, from fallout, 1.45 minutes is immaterial. Beacuse this time and distance is small, for the purpose of this example, use the time of H + 4 for the platoon to enter (Te) the contaminated area.
Step 3. Set up the remainder of the problem in the following manner--
IDt = TF x D.
IDt = inside total dose received
TF = transmission factor for HMMWVs (see Table 6-1)
D = total dose received (unshielded). Visualize the problem of finding D (total dose):
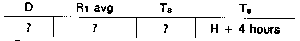
R1 avg = average R1 value
Ts = time of stay in contaminated area
Te = time in which unit enters the contaminated area
In this example, use H + 4 as the Te value.
Step 4. Referring back to Figure 6-16, the highest dose rate the platoon is expected to encounter is 100 cGyph--used as the R1 max, because it is the highest known dose rate along the MSR. Unless a survey actually establishes the actual R1max, use the known dose rates found on Te overlay graphics. Calculate the R1 average for the problem:
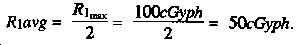
Now, go back to the visualization in Step 3, and plug in the value for R1 avg.
Plug into the visualization (Step 3) the value for TF from Table 6-1.
Step 5. Measure the map distance from Point A (intersection of the 20 cGyph contour line and the MSR) to Point B, where the platoon will exit the contamination. This distance should equal approximately 1.4 kilometers. Time of stay (Ts) is calculated as follows:
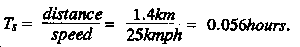
Step 6. Turn to Figure 6-12, the total dose nomogram for a decay rate of 1.2. Align the hairline across the Te value of H + 4. Again, find that the Ts value is less than 1 hour. As described earlier, place the hairline on 1. Pin the hairline down on the index scale (middle scale); and rotate the hairline so that it crosses the R1 scale at the R1 value of 50 cGyph. Read the value in the far left-hand column labeled Total Dose (D). Again, this value is off the printed scale.
In this case and all similar cases in which the hairline falls off the scale, there are two ways to solve the probelm. First method is to multiply the R1, avg value (50 cGyph) by 10. When rotating the hairline on the index scale, lay the hairline across the new R1 avg value of 500 cGyph. Read adjusted total dose from the far left-hand column. In this case, that dose is approximately 80 cGyph. Divide this number (80 cGyph) by 10 to find actual dose--in this case, 8 cGy. The second method is to multiply the R1 value by the index value where the hairline crosses the index scale. Both methods are correct, and the preferred method is left to the individual. Place this value in the visualization.
Step 7. This dose (8 cGy) is the dose for a Ts of 1 hour. In this problem the Ts value was 0.056. To determine the actual outside, unshielded dose in this area, multiply the dose by the Ts:
|
D adj |
= D x Ts |
|
= 8 x 0.056 |
|
|
D adj |
= 0.448 cGy. |
So, for this problem the actual unshielded dose the soldiers may receive is leas than 1 cGy or 0.448 cGy. However, the soldiers are in HMMWVs.
Step 8. Multiply the dose (0.448 cGy) by the transmission factor for HMMWVs (0.6) to calculate the inside, shielded dose rate the soldiers can expect to receive:
IDt = 0.448 cGy x 0.6
= 0.2688 or 0.3 cGy.
Soldiers of the chemical platoon are expected to receive 0.3 cGy, or leas than 1 cGy, during their movement. Keep in mind that this calculation is based on a HMMWV transmission factor that was obtained using a radioactive source that is almost twice as strong as average fallout. So, the actual dose the soldiers receive may be less.
To answer the brigade S3's question, give the final dose the soldiers will receive. The S3 does not want to know how you arrived at those numbers--just the information. In this case, the soldiers are expected to receive 0.2688 cGy. As stated originally, the platoon is rated at RES-1 moderate risk. Refer to Appendix A to determine the risk value. From Table A-2 in Appendix A, moderate risk for RES-1 units is less than or equal to 30 cGy. Add the expected dose of 0.2688 or 0.3 cGy to determine what RES category the platoon will be in after its movement. The answer to the brigade S3's question is "Yes," the platoon can accomplish the move without exceeding 70 cGy total exposure. No additional protective measures are required other than to cover the nose and mouth with a cloth or wear the protective mask to protect the respiratory track from airborne radiological contaminants. If for some reason (enemy activity, vehicle breakdown, etc.) the platoon has to extend its stay in the area, new calculations must be made using the new value for Ts.
If the actual dose received by the platoon were to exceed the prescribed dose, you should suggest they either delay the platoon's entry into the area, increase the traveling speed of the vehicles, or add shielding to the vehicles (see Appendix B for adding shielding). In some cases all three steps outlined here may be used to reduce the dose received and meet mission requirements.
To calculate the time of exit (Tx) in this problem, or exactly when the platoon must exit the area, use the following formula:
Tx = Te + Ts.
Application of Avoidance Principles
The concepts presented in this chapter can be applied to the integrated battlefield. To do this, you use the checklist in Appendix G as a guide for tactical operations.
ANBACIS System
As discussed in Chapter 2, ANBACIS is a computer system capable of generating NBC warning and reporting messages; but the system also is capable of calculating EDMs and radiological calculations for total dose, crossing problems and induced radiation.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|