Appendix B
Shielding
Shielding reduces the effects of gamma radiation on personnel and equipment. Metal, concrete, soil, water, and wood are good shielding materials. The denser the material, the better the shield. Low-density materials are as effective as higher density materials when the total thickness of the low density material is increased. Density is defined as the number of molecules per unit of volume. The denser a material, the better shield it makes.
It is not possible for gamma radiation to be completely absorbed. However, if enough material is placed between the individual and the radiation source, the dose rate can be reduced to negligible proportions.
The three types of radiation which we try to shield against are as follows:
Alpha Radiation -- A helium nucleus, stripped of its electrons, that travels only a few centimeters in air (5-10 cm) and is an internal hazard only.
Beta Radiation -- A very high speed electron that travels a few meters in air, but has limited penetrating power. Beta radiation is an external hazard and internal hazard.
Gamma Radiation -- Pure energy traveling at the speed of light. Gamma can never be totally shielded out, but can be reduced to insignificant or negligible levels.
To determine the effectiveness of shielding, you must calculate the dose rate (inside or outside) based on the density and thickness of a given shield. This calculation requires determining the half-thickness or total thickness of a particular shielding material.
Principles
Density -- Mass (number of molecules per unit of volume). The denser a material, the better shield it makes.
Half-thickness -- The amount of material required to reduce the dose rate by one-half.
Total thickness -- This is the actual thickness of the shielding material.
Position of the shield -- The closer the shield is to the source the better.
Dose rate build-up -- This is produced by the shield. The shield causes radiation to scatter; therefore, the closer you are to the shield the higher the dose rate.
Materials
Earth. The most common shielding material. About one foot of earth makes a very adequate shield.
Concrete. About 6 to 8 inches of concrete makes a good shield.
Steel. Tanks and (USMC) amtracks are very good shields against radiation.
Buildings. Wood or brick buildings make good shields.
Effectiveness
The effectiveness of a given material in decreasing radiation intensity is measured in units of half-value-layer thickness, or half-thickness. This unit is defined as the thickness of any material which reduces the dose rate of gamma radiation to one-half its unshielded value. Thus, if a soldier were surrounded by a 6-inch concrete wall (6 inches is the half-thickness of concrete) and the gamma radiation outside were 200 cGyph, he or she would receive gamma radiation at the rate of 100 cGyph. The addition of another 6 inches reduces the rate to 50 cGyph. Each succeeding half-thickness of concrete would, therefore, reduce the radiation dose by one-half.
Problem: How many half-thicknesses of the above concrete wall reduce the radiation dose to 25 cGyph?
Solution: Beginning with the rate of 200 cGyph, the first half-thickness reduces it to 100 cGyph. The second half-thickness reduces the dose rate to 50 cGyph, and the third to 25 cGyph. Three half-thicknesses (18 inches) of concrete meets the requirement.
Mathematical Method
A series of computations are necessary to determine shielding requirements. The following symbols represent unknown values. An equation accompanies each to allow a better understanding of what each represents.

Sample problem, using mathematical method:
Sample problem, using the same method with the (2n table): Use Table B-1 to simplify the process. Table B-1 includes directions for extrapolating safe-sided values not listed in the table. Table B-1 eliminates the need for logarithms, graph paper, or slide rule.
|
Table B-1. 2n values and guide for siding 2n values (right) |
|
Editor's Note: This graphic is not viewable in HTML format. Check "Download Document" at top of this file for an alternate format or obtain a printed copy of the document. |
Sample Problems
Problem: Find the final dose rate with a known amount of shielding.
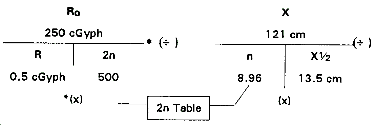
Situation: You are in a bunker after a nuclear detonation and need to know what final dose rate you will receive. The initial dose rate with no shielding (Ro) is 2,000 cGyph. The total thickness of the shielding material (X) is 31 centimeters. The half-thickness of the shielding material (X 1/2) is 4 centimeters. What is the final dose rate resulting from the shielding?
Ro = 2,000 cGyph
X = 31 cm
X1/2 = 4 cm
Find: R
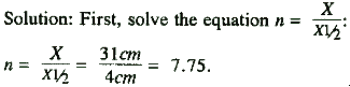
Enter Table B-1 in the n column and find n = 7.7 and 7.8. Go to Table B-1. You are looking for R, and you entered with n; so, select the smaller n value of 7.7. Read the corresponding 2n value of 206. Apply the equation
Figure B-1, below, shows the key strokes for algebraic notation system calculators.

Note: Solutions based on calculator key strokes will always be smaller than those based on the 2n safe-siding table, as a mathematical formula is more accurate than a nomogram.
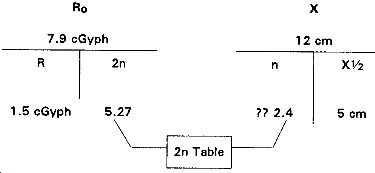
Situation: R = 1.5 cGyph X = 12 cm X 1/2 = 5 cm.
Find: The outside dose rate.
Situation: R = 1 cGyph Ro = 120 cGyph X = 24 cm.
Find: The half thickness for the shielding material.
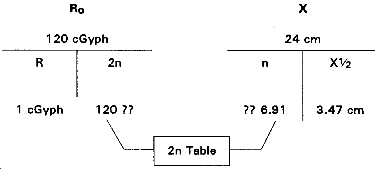
*Note: When working any problem with the mathematical method, a horizontal line means you divide; a vertical line means you multiply.
Having found the half thickness for the shielding material in the problem above, the NBC officer wants to know how much material is needed to reduce a dose rate of 25 cGyph down to .5 cGyph.
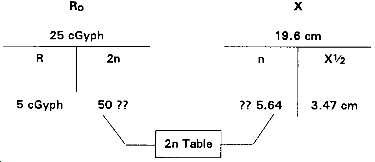
The bunker you are in has two feet of sandbags on it. A monitor has reported a dose rate reading of 36 cGyph outside. The commander has taken the monitor on a trip to the division Command Center. The NBC Officer must report the inside reading to the battalion XO in ten minutes. Division NBC has reported that 4.7 inches of the local earth in sandbags will reduce a dose rate in half.
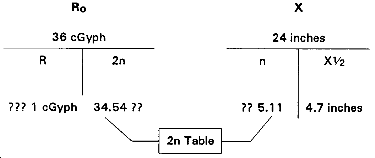
Problem: Find the half thickness, using the 2n table.
Situation 1: An initial dose rate with no shielding (Ro) was 1,000 cGyph. The total thickness of the bunkers shielding material (X) is 27 cm. A final dose-rate (R) received inside the bunker was 7.60 cGyph. What is the half thickness of the bunkers shielding material?
Ro = 1,000 cGyph
X = 27 CM
R = 7.60 cGyph
Find: X½.
Solution:
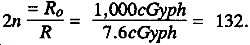
Enter Table B-2 in the 2n column and find 2n equals 128 and 136. Table B-1 directs use of the smaller 2n of 128. Read corresponding n value of 7.0.
Apply the equation:
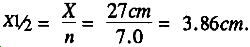
Problem: Find total thickness of shielding.
Situation 2. You reported an initial dose rate with no shielding (Ro) of 500 cGyph after a nuclear detonation. Your shielding material has a half-thickness of 7.5 cm (thickness of material necessary to degrade gamma radiation dose by one-half).
For safety, you desire no more than 1 cGyph exposure inside a bunker. What thickness of shielding material is needed to protect the occupants?
Ro = 500 cGyph
X½ = 7.5 cm
R = 1 cGyph
Find: X.
First, solve for 2n:
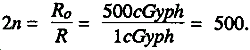
Enter Table B-2 in 2n column, and find 2n is between 480 and 512. Table B-1 directs use of the larger 2n of 512. Read the corresponding n value of 9.0. Use the equation X = (n) (X-1/2X = (9.0) (7.5 cm) = 67.5 cm.
Problem: Find the initial dose rate with no shielding.
Situation 3: A bunker has a total thickness of 12 cm shielding material (X). The half-thickness of the shielding material (X-1/2) is 6.25 cm. From inside the bunker, a final dose-rate (R) of 5 cGyph is read. What was the initial dose rate with no shielding (Ro)?
X = 12 cm
X½ = 6.25 cm
R = 5 cGyph.
Find: Ro.
Solution:
First, solve the equation for n:
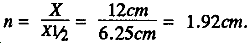
Enter Table B-2 in the n column, and find n is between 1.9 and 2.0. Table B-1 directs use of the larger n value of 2.0. The corresponding 2n value is 4. Utilize the equation Ro = (2n) (R)
Ro = (5 cGyph) (4.0) = 20 cGyph.
Transmission Factors
Transmission factors are used in radiation calculations to determine the impact of shielding on radiation exposure. TFs are simpler and preferred when the half thickness and total thickness are not important, and only the actual reduction of the dose rate is the primary consideration. Transmission factors are always less than 1.
Determination of Transmission Factors
TFs are calculated using the following formula:
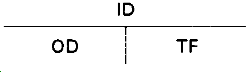
ID = inside dose, or dose rate.
OD = outside dose or dose rate.
TF = transmission factors.
Sample Problems
Situation: ID = 66 OD = 550.
Find: TF.
Solution: 66 ÷ 550 = .12.
Situation: ID = 45 OD = 120.
Find: TF.
Solution: 45 ÷ 120 = .375.
Situation: You are inside a tank with a reading of 45 cGyph, and you have recorded an outside reading of 1,125 cGyph. What is the TF for the tank?
Solution: 45 ÷ 1125 = 0.04.
Exercise Problems
In the table below are half-thicknesses for some common materials (These values will be used in solving the problems that follow.):
|
Material |
Half-thickness (inches) |
|
Steel |
0.7 |
|
Concrete |
2.2 |
|
Earth |
3.3 |
|
Wood |
8.8 |
Problem: The outside dose rate of residual radiation in a radiologically contaminated area is 400 cGyph at H + 1.
Find: What would be the dose rate inside a concrete bunker if the walls were 10 inches thick?
Solution:
Ro = 400 cGyph.
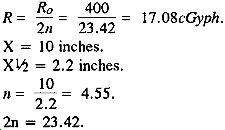
Find: What would be the dose rate if you added 1 foot of earth cover to the bunker?
Solution:
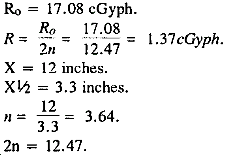
Find: What would the dose rate be inside a tank with 3 inches of armor plating (steel)?
Solution:
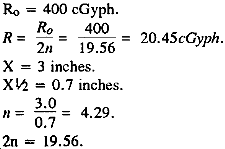
Problem: In the same radiologically contaminated area, the dose rate has decayed to 180 cGyph at H + 2 hours. Which of the following would offer you more protection from the radiation: a wooden building with 2-inch walls; a concrete bunker with 6-inch walls; a foxhole with 12 inches of earth cover?
Solutions:
Building: Ro = 180 cGyph.
R = ?
X½ = 8.8 inches.
X = 2 inches.
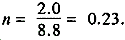
Bunker: Ro = 180 cGyph.
R = ?
X½ = 2.2 inches.
X = 6 inches.
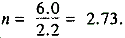
Foxhole: Ro = 180 cGyph.
R = ?
X½ = 3.3 inches.
X = 12 inches.
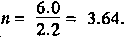
Answer: A foxhole with 12 inches of earth cover would give the best protection.
Note: The higher the n, the higher the 2n; so, the better the protection. The higher 2n divided into the Ro will result in a smaller R.
Problem: You are located in a tank in a radiologically contaminated area. The dose rate inside is 75 cGyph. The tank has approximately 2 inches or armor plating (steel).
Find: What is the approximate outside dose rate?
Solution:
Ro = 6.95 x 75 = 521.25 cGyph.
R = 75 cGyph.
X½ = 0.7 inches (from Table B-3).
X = 2.0 inches.
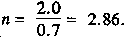
2n = 6.95 (from Table B-1).
The guide for safe-siding depends on the unknown variable. For example, if the thickness is unknown, find X in the unknown column, read to the right. Enter the table with 2n, select the larger value of 2n, and leave with the value of n corresponding to that larger value.
Note: Gamma radiation energy varies.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|

