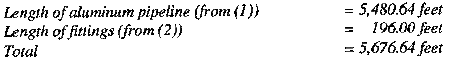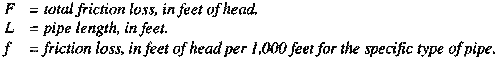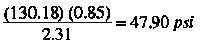| Chapter Four. Design |
4-1. Characteristics of Petroleum Fuels. The fundamental characteristics of fluids must be considered when designing petroleum pipeline systems. However, only the physical properties as they affect the storage of military fuels in terminals and their flow through pipelines are to be considered. These characteristics are weight density, specific gravity, American Petroleum Institute (API) gravity, viscosity, temperature, and pressure.
a. Weight Density. Density is a measure of the concentration of matter, weight is a measure of the force of gravity. Weight density is the weight per unit of volume. Added weight makes fluid movement more difficult. The densities of fluids are at the freezing point of water and under one atmosphere of pressure (the pressure at the earth's surface). The density of water is 62.4 pounds per cubic feet.
b. Specific Gravity (SG). Specific gravity is the ratio of the weight of a volume of liquid to the weight of an equal volume of water. For example, a cubic foot of diesel fuel weighing 53.04 pounds has a specific gravity of 0.85 (53.03 divided by 62.4).
c. API Gravity. The API gravity scale, used by the petroleum industry, is based on reciprocals of specific gravities and, therefore, produces whole numbers having a greater numerical spread. The API scale is in degrees API and has a range of 0 to 100 degrees. Water is referenced as standard and is assigned an arbitrary gravity of 10 degrees API. This gives a spread of 90 degrees API between the heaviest and lightest petroleum products. API gravity is inversely proportional to specific gravity: the lower the specific gravity, the higher the API gravity. Thus, petroleum products that have the lightest weight have the highest API gravities. The standard temperature for expressing API gravities is 60°F. So, gravities taken at other temperatures must be corrected to 60°F.
(1) Conversion Formulas. Use the following formulas to convert between API gravity (at 60°F) and specific gravity:

(2) Design Fuel. This is the fuel type for which a pipeline system is designed. Military pipelines most likely will transport diesel and jet fuels and kerosene. Federal specifications list the properties of these fuels. Table 4-1 shows the gravity range of the most common military fuels. The spread between the heaviest and lightest fuels is 34 degrees API. Because of this spread, specific gravity is an important factor in the design of military pipelines. The anticipated quantities of different fuel types to be pumped must be considered. The heaviest fuel is the design fuel, which makes up 25 percent or more of the total requirement. Under normal conditions, a pipeline designed for diesel fuel can handle other fuels effectively. Further discussion is based on diesel fuel that has an average specific gravity of 0.8967 (26.3 degrees API). This provides a basis for comparison of capacity and performance when heavier or lighter products are to be moved.
d. Viscosity. Viscosity is a measure of the flow of a liquid. It is the internal force (resistance) or opposition to flow. The greater the internal force, the more viscous the liquid. Since a viscous liquid resists efforts to move it, absolute viscosity is defined as a measure of the force required to produce flow. In the electric system, the unit of absolute viscosity is the poise, which is equal to one dyne-second per square centimeter (100 centipoises). Viscosity and specific gravity are related; the relationship is expressed as kinematic viscosity, which is the ratio of absolute viscosity, in poises, to specific gravity of the liquid. The unit of kinematic viscosity is the stoke given in units of square centimeters per second (100 centistokes). Viscosity in stokes multiplied by specific gravity equals viscosity in poises. The viscosities of military fuels are found in Appendix C or in federal specifications.
e. Temperature. The above characteristics are affected by temperature. Volume and API gravity increase with temperature while density, specific gravity, and viscosity vary inversely. Because of these effects of temperature, all measurements are corrected to 60° F. This is the standard temperature for both design and operation of military pipeline systems. Correction factors are found in Appendix C.
f. Pressure. In pipeline design, the elevation of fuels from one level to another, their movement from place to place, or both are governed by the principles of hydraulics. In the military pipeline system, the areas of interest are the--
- Behavior of liquids at rest (hydrostatic pressure and equilibrium), as in a storage tank or slack line.
- Forces exerted on liquids by objects in motion (hydrodynamics), as in pumping equipment.
In actual application, all forces that produce pipeline flow and those opposing it can be described or measured in terms of pressure or head. Coupled military pipelines are low-pressure systems that operate at a normal working pressures of no more than 740 psi. Low-pressure pipelines require that pumping stations be spaced closer than high-pressure lines to get the same throughput. Lighter pipe, used in low-pressure pipelines, is easier to construct, and it avoids the mechanical failures inherent at higher pressures. However, welded military pipelines can operate at higher pressures. Head (or pressure) in a pipeline is either static or dynamic. However, you must consider atmospheric pressure and vapor pressure.
(1) Static Head. Static head is a measure of pressure in liquids at rest. It is also a measure of potential energy (energy of position). Static head is the vertical height from a given point in a column or body of still liquid to its surface (usually expressed in feet). To calculate the pressure in water, use the following formulas, which are also found in Appendix A:

Because of their lower specific gravities, static pressures of petroleum products are proportionally less.
(2) Dynamic Head. Dynamic head is a measure of pressure, or kinetic energy, of liquids in motion. Figure 4-1 shows the relationship between static head and dynamic head. The distance from the liquid level in the tank to ground level is the static head. As liquid starts to flow down the pipe, it loses static head but gains velocity and dynamic head. Dynamic head is greatest at the ground level where the flow changes direction and the streams begin to rise in the air. After that, dynamic pressure or head decreases until all velocity is lost. During this action, the stream recovers some of its initial static head. The difference between the initial static head and the final static head or dynamic head is the head loss, which represents friction losses due to pipe and air. In summary, dynamic head is equal to the static head required to accelerate the flowing velocity of the stream.
(3) Atmospheric Pressure. Atmospheric pressure is comparable to static pressure in liquids because it is caused by the weight of air above the earth's surface. Atmospheric pressure is about 14.7 psi at sea level. It decreases somewhat at higher altitudes. The maximum suction lift is about 33.96 feet of water (14.7 x 2.31 = 33.96). Because elevation affects atmospheric pressure, pump engines are affected at elevations above 3,000 feet, and design loads on pumps are decreased about 4 percent per each 1,000 feet above 3,000 feet.
(4) Vapor Pressure. All liquids, particularly light fuels, have a tendency to vaporize. This tendency (volatility) increases with temperature and decreases with pressure. The vapor pressure of a system is a function of the temperature and pressure of the system. However, the effect of total pressure on the vapor pressure is small, so the vapor pressure of a system is usually regarded as a function of temperature only. Vapor pressure begins to exceed atmospheric pressure at the boiling point of a liquid. The boiling point varies; at high altitudes, liquids boil at lower temperatures than at sea level. Vapor pressure reduces the effect of atmospheric pressure acting on a liquid and affects pumping operations involving suction lift.
Figure 4-2 shows the theoretical suction-lift values for military fuels. The height of the bar graphs shows the maximum net suction lift for water and petroleum products after vapor pressure has been deducted from atmospheric pressure. For example, Figure 4-2 shows that diesel at normal atmospheric pressure (14.7 psi) theoretically can be lifted, by suction, over 38 feet at 50° F, about 35 feet at 100° F, and about 33 feet at 200° F. If atmospheric pressure is reduced, the net maximum suction lift also will be reduced. To show this, reduce the atmospheric pressure 3 pounds below normal. Lay a straight edge on the chart with one end on the point representing 3 psi on the atmospheric scale and keep the edge parallel to the baseline. The reading should show that 3 psi atmosphere equals 9 feet suction lift for Type A motor gasoline (MOGAS). Comparatively, Type A MOGAS cannot be lifted this distance by suction at 135°F, and the net lift at 100°F and 50° F is reduced to 7 feet and 21 feet respectively (16-9 and 30-9). Therefore, normal suction pressure of 20 psi should be increased to 30 psi for operating temperatures over 100°F. (Special conditions from those just described apply to station 1 on a pipeline.)
4-2. Pipeline and Pumping-Station Data.
a. Pipelines.
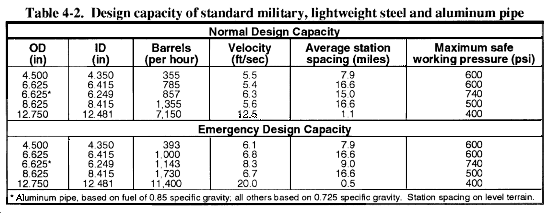
(1) Capacity. Pipeline capacity (throughput) is the quantity of fuel pumped per unit of time. Generally, it is expressed in barrels per hour (BPH) or GPM. One barrel is equivalent to 42 US gallons. Table 4-2 shows the normal and emergency capacities of military pipelines. Normal capacities are used for pipeline designing.
(2) Flow Velocity. With a specified pipe size and a given throughput requirement, the flow velocity is constant for all practical design purposes, using average conditions of climate and topography. See Table 4-2 for average velocities of flow, in feet per second.
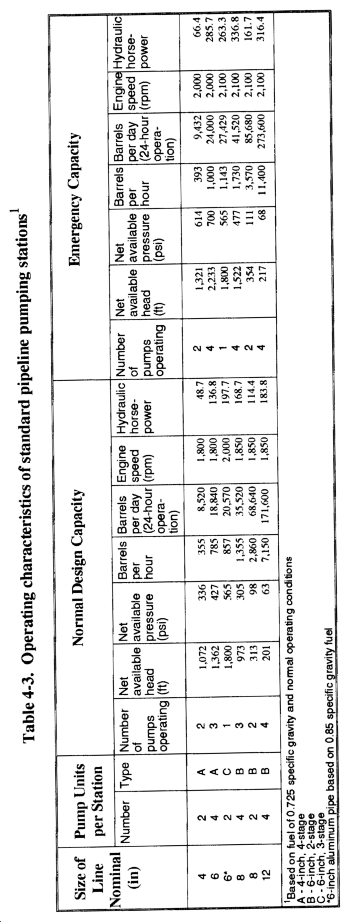
(3) Pipeline Pumping Pressures. Normal working pressures are used in pipeline design. Emergency capacities are dictated by the tactical situation. Table 4-2 lists safe working pressures for lightweight pipe or tubing. These safe working pressures are based on the yield point of the pipe material and provide a designed minimum safety factor of 3.0. Table 4-3 lists pipeline pumping pressures for normal and emergency design capacities.
(4) Flow Resistance. A liquid's resistance to flow in a pipeline results from the following: Friction of the pipe walls. Viscosity of the liquid. Special factors such as entrance to the pipe, sudden changes in flow direction or cross-sectional area, flow through equipment like traps and meters, and corrosion or deposits in the line. Resistance usually is expressed in terms of the pressure required to overcome resistance, in psi or in feet of head of the liquid pumped.
- Friction of the pipe walls.
- Viscosity of the liquid.
- Special factors such as entrance to the pip, sudden changes in flow direction or cross-sectional area, flow through equipment like traps and meters, and corrosion or deposits in the line. Resistance usually is expressed in terms of the pressure required to overcome resistance, in psi or in feet of head of the liquid pumped.
b. Head Capacities of Pumping Units.
(1) Normal Head Capacity. The normal head capacity (see Table 4-3) of a pumping unit is the total head against which it will pump at the most efficient operating point. The head capacity for a particular pump varies according to its design efficiency. Head capacity is a function of speed (operation), in RPM versus its rate of discharge (GPM). In other words, the design speed of the pump unit (RPM) must be considered together with the required head and desired throughput (GPM) to establish maximum efficiency in pipeline design.
(2) Emergency Head Capacity. Emergency head capacity (see Table 4-3) of a pumping unit is the total head against which it will pump to provide maximum pipeline capacity. Maximum head capacity is for emergency operation only and is never used as the basis for design. Pumping stations should operate at maximum head capacity only during critical tactical emergencies.
NOTE: For convenience, all operating graphs for military pump units are in Appendix C.
c. Use of Pumping Unit Operating Graphs. Pumping unit operation graphs (performance curves) graphically display the interrelationship between pressure (in feet of head and/or psi), pump speed, and throughput. From these graphs, you can estimate the pumping unit's operating speeds, the volume of fuel throughput, or the operating head as long as you know two of the three factors.
For example, to determine the throughput of 0.85 SG fuel moved by a 6-inch, 3-stage, 800-GPM mainline pump (IPDS), operating at 1,800 RPM with a dynamic head loss of 500 psi or 1,360 feet of head, proceed as follows:
(a) Find the pumping unit operating graph for the specific pump in Appendix C.
(b) Determine the dynamic head loss, in psi and feet, for the fuel type and enter the chart from the left side.
(c) Draw a horizontal line from the dynamic head loss to the established pump speed.
(d) Draw a vertical line at the point where the horizontal line intersects the pump-speed curve. Exit the chart at the bottom to determine throughput, which is 500 GPM.
d. Friction Loss. The two sources of friction within a pipeline system are friction resulting from fluid flowing through the pipe and friction created by fuel passing by obstructions, such as valves, fittings, and pipelines of smaller diameters. The total friction loss in a section of pipeline, usually expressed in feet of head per unit of pipe length, is the total of the two friction losses. The total friction loss represents the total energy, or head, expended in moving the fuel through a pipeline. In design, this information serves as a parameter on which to base the distances between pumping stations on level terrain. You can calculate friction loss by using the Darcy-Weisbach equation shown in Appendix A or the graphs in Appendix C.
(1) In Pipes. Pipe friction loss arises from the internal friction of the particles of the fluid itself (viscosity) and the resistance to flow at the pipe-wall surfaces. The viscosity of a fluid indicates the friction expected from a given flow.
(2) From Fittings. Friction loss through fittings results from the same surface friction as losses in straight pipe. Such losses for all fittings except plug valves are determined by converting each type fitting into its equivalent pipe length and then determining the friction loss. To do this, find the intersection of a straight line between the valve type and the inside pipe diameter scales in the equivalent pipe length of pipe fittings chart in Appendix C. Determine the friction loss for the equivalent pipe length as discussed above. Table 4-4 shows the approximate pressure loss through lubricated plug valves.
|
Problem and Solution #1 Calculate the friction head loss per mile to move gasoline in an aluminum pipeline with an ID of 6.249 inches. The pipeline design requires one check valve and one gate valve every mile and U-loop expansion devices every 1,000 feet of pipeline. The design flow rate is 550 GPM. Use the following computations to solve the problem: Step 1. Pipe Length
Step 2. Pipe Length Equivalents for Pipe Fittings.
Step 3. Pipe Length and Fittings.
Step 4. Friction Loss in Pipe and Fittings. Find the head loss due to friction chart in Figure C-9. Enter the chart at the bottom with the design flow rate of 550 GPM. Draw a vertical line up until it intersects the slanting line marked 6.249 (the ID of the aluminum pipe). From this intersection, trace a horizontal line to the friction loss scale on the left side of the chart. On this scale, the friction loss in feet of the head per mile should be 90. Use the following equation to compute the friction loss equivalent length of 5,676.6 feet:
|
f. Reducing Friction Loss. Reducing friction loss may be required when design errors or other factors, such as terrain or time, have led to the placement of pumping stations too far apart to maintain the design flow rate. The three remedial methods for reducing friction loss are using larger pipe, using double-looped lines, and reducing the flow rate.
(1) Using Larger Pipe. If a problem is anticipated and material is available, using larger pipe to reduce friction loss will save time and work; you will not have to lay the line twice. The following problem and solution shows how to use the larger-pipe method for reducing friction loss:
|
Problem and Solution #2 The friction loss in a 1,786-foot section of 6 5/8-inch steel tubing must be reduced to a maximum allowable head of 18 feet under maximum emergency flow conditions. Maximum emergency rate of flow is 928 BPH. You must determine the maximum length of 8 5/8-inch tubing required to reduce the head loss to 18 feet. Solving this problem is based on the principle that total head or pressure loss in a section of pipeline, which consists of two sizes of pipe in series, is equal to the sum of the friction losses for each size and length of pipe. The following equation explains the principle: F = L1(f1) + L2 (f2) where--
The total friction loss must be no greater than the maximum allowable 18 feet of head. L1 is the length of the 8 5/8-inch tubing, n units of 1,000 feet. L2 is the length of the 6 5/8-inch tubing, in 1,000 foot units, and equals 1.786 minus L1. Convert the maximum flow of 928 BPH to 650 GPM and use 8.415 inches (as ID of 8 5/8-inch tubing) to determine that the friction loss per mile is 29 feet. Convert this to friction loss (f1) per 1,000 feet by dividing 29 feet per mile by 5.28 (thousand feet per mile) which equals 5.5 feet of head loss per 1,000 fee. For a flow of 650 GPM and an ID of 6.415, f2 is equal to 21.8 feet of head loss per 1,000 feet. Using the base formula and the above figures, solve for L1 as follows:
|
(2) Using Double Lines. If larger pipe is not available, you can reduce friction loss by laying additional pipe parallel to the first and connecting the two. The following problem and solution demonstrates this method:
|
Problem and Solution #3 The conditions are the same as for the larger-pipe method; however, you are to determine the length of double line necessary tot reduce the head loss to 18 feet. Use the same base formula in solving this problem. Before starting, you must determine how to compute the friction loss (f1) for length (L1) of double line. The principle is that the flow rate in each half of a double line is considered to be half that of a single line of the same length. As before, the total friction loss must be no greater than the maximum allowable 18 feet of head. L1 is the length of double 6 5.8-inch line required. L2 is the length of one 6 5/8-inch line in 1,000-foot units and equals 1.786 - L1. The friction loss for the double line is half the emergency rate (928 BPH) or 464 BPH. Convert 464 BPH to 325 GPM and use 6.415 inches as the ID to determine that f1 equals 31 feet of head loss per mile or 5.87 (31/5.28 feet of head loss per 1,000 feet of double line. For a flow of 650 GPM and an ID of 6.415, f2 equals 21.8 feet of head loss for each 1,000feet of single line of 6 5/8-inch steel tubing. Using the base formula and the above figures, solve for L1 as follows:
|
g. Spacing of Pumping Stations. An important element in the design of a military pipeline system is pumping-station spacing. The spacing is determined by the hydraulic designs and the pump-unit capabilities. The hydraulic design considers the friction head loss in the pipe and changes in elevation of the pipeline when it operates at normal design capacity. When a pipeline runs uphill, the stations are closer together; when it runs downhill, the stations are farther apart. The distance between pumping stations is based on the friction head loss over distance, which is increased or decreased based on changes in terrain. The key factor in pumping-station placement is that all pumping stations are in balance hydraulically and are operating at the same rate (even work-load distribution). Table 4-2 shows the average spacing of pumping stations on level terrain for various sizes of pipelines, based on maximum safe working pressures. The design factors that determine pumping-station spacing are the--
- Topographic features of the pipeline route.
- Type and properties of the design fuel (viscosity).
- Required suction pressures, available head capacities, and other operating characteristics of the pumping unit.
- Friction head losses based on flow rate for the selected size of pipe and fittings.
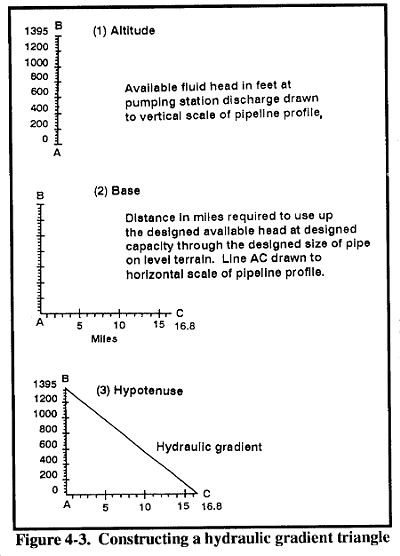
h. Modular Design. Modular design is a simplified graphical method of locating pumping stations (except station 1) and pressure-reducing stations. This method is essentially the solution of hydraulic calculations by means of graphs. The graphs required area profile of the pipeline route and the hydraulic gradient triangle.
The hydraulic gradient triangle is a right triangle that is constructed on the same scale as the profile. The triangle's altitude (vertical distance) represents the available feet of head pressure at the discharge of the pumping station. The base (horizontal distance) represents the distance that the fluid can be moved on level terrain, which is based on the available head of the pumping unit, the friction head loss in the pipeline, and the design flow rate.
The hypotenuse of the triangle, the result of a vector diagram, is the hydraulic gradient. This gradient represents the rate of head loss due to friction for a specific pipe size carrying a specific fluid at a specific rate of flow. If the pipe size, type of fluid, or flow rate is changed, a new triangle must be constructed. Generally, when this triangle is applied to the pipeline profile at the same scale, with the right angle corner on the location of one pumping station and with the base parallel to the base of the profile, the point at which the hypotenuse (hydraulic gradient) or its extension intersects the profile is the maximum distance to the next pumping station.
The modular-design method is accurate enough for most tactical situations. A more exact method of determining friction head loss and the energy relationship for liquid flowing through a pipe between two points can be calculated by the Darcy-Weisbach and Bernoulli equations (Appendix A). A complete hydraulic analysis should be prepared to verify the modular design as time permits.
i. Construction of the Hydraulic Gradient Triangle. You can construct this triangle from transparent plastic sheets, cardboard, or paper thick enough so that after trimming, each edge can be used as a straight edge. The following problem and solution shows how to construct a typical hydraulic gradient:
|
Problem and Solution #4 You are to construct a hydraulic gradient triangle for a pipeline with normal design capacity of 550 GPM for diesel fuel at 60oF. You will be using a 6-inch, 3 stage, 800-GPM, mainline pumping unit and 6.625-inch (6.249-inch ID) aluminum pipe. The normal design head capacity of each pump unit is 1,800 feet. Two pumps make up a standard aluminum system pumping station. The pipeline profile has the following scale: vertical, 1 inch equals 200 feet; horizontal, 1 inch equals 2 miles. Construct the triangle with a 90-degree angle at A as follows: Step 1. Draw the altitude (AB) of the triangle to the same scale as the vertical scale of the pipeline profile in Figure 4-3. The height represents the available fluid head in feet at design rate of flow at the pumping-station discharge. The height is graduated in suitable units, usually 10 feet. See Table 4-3 for the design capacity for this pump. The available head capacity is 1,800 feet. This is the altitude of the hydraulic gradient triangle. The scale is 1 inch equals 200 feet, so the altitude is 9 inches. Step 2. Draw the base (AC) of the triangle to the same scale as the horizontal scale of the pipeline profile shown in Figure 4-3. The length represents the distance, in miles, that the available discharge head of the pumping station can move the fluid at normal design rate of flow on level terrain. To determine the length, divide the available head of the pumping station by the friction loss per mile for the specific tubing at the specific design flow rate. Step 3. Use Figure C-9 to find the friction head loss at 550 GPM in an aluminum pipeline (6.625-inch ID). The friction head loss is 97 feet per mile. However, the friction head-loss factor is for gasoline at 60o F and must be corrected for diesel, multiply 97 by 1.09 to get 105.7 feet of head loss. Divide the available head by the head loss per mile to get a distance of 17 miles (1,800/105.7). This is the base of the hydraulic gradient triangle. The scale is 1 inch equals 2 miles, so the base is 8.5 inches. Step 4. The hypotenuse (BC) of the triangle is the straight line that connects points B and C (see Figure 4-3). This slope represents the loss of head per unit length of pipeline and establishes the gradient for determining station spacing. |
4-3. Location of Pumping Stations.
The following paragraphs describe the factors considered in locating mainline pumping stations and flood or suction stations for military pipelines. Mainline pumping stations, with the exception of station 1, are placed by the modular method described above. Locations of other pumping stations require special analysis for each station site.
a. Pumping Station 1. This station (base terminal) receives fuel from a petroleum-terminal tank farm or host-nation supply. Station 1 is located as far from the tank farm as possible for safety and convenience of operations. Because of its critical position, the station and the connecting line to the tank farm require careful planning and design to ensure that sufficient suction pressure is provided to the first mainline pumping station under design-flow conditions. The suction pressure at station 1 should be at least 20 psi. If the required suction pressure for station 1 cannot be created by gravity, a flood or suction pump is required.
(1) Gravity System. In determining whether gravity will furnish sufficient suction pressure for station 1, proceed as follows:
(a) Select a tentative site for the station, the elevation of which is below the outlet of the lowest tank in the tank farm.
(b) Determine the available head from gravity by computing the difference in elevations of the tank outlet and the pump-suction manifold entrance at the proposed pumping station.
(c) Calculate the total friction loss in feet of head for the pipe and fittings used to connect the tank to the pumping station for the design flow conditions. Make sure that friction loss is corrected for design fuel.
(d) Determine the net head available at the station by subtracting the friction head loss at the design rate of flow from the head available from gravity.
(e) Convert the net available head to suction pressure in psi by using the conversion formula in Appendix A. When the suction pressure is greater or equal to 20 psi, the mainline station 1 can be fed by gravity flow from the tank farm.
(2) Alternative Methods. If gravity does not furnish enough suction pressure at any suitable site for station 1, determine if using the larger-pipe method or the double-line method will reduce friction loss enough to eliminate the need for a flood or suction pumping station. If analyses show that gravity feed with either method will not provide enough suction pressure, then install a flood or suction pumping station.
|
Problem and Solution #5 The outlet of the lowest tank in the petroleum tank farm is 150 feet higher than the pump suction manifold entrance of proposed station 1. The suction pressure required at station 1 is 20 psi. Connections between the tank and the pumping station consist of 680 feet of 6.249-inch ID aluminum pipe, two gate valves, five 45-degree elbows, two 90-degree elbows and two through-run T s. The design flow rate of the pipeline is 650 GPM of 0.85 specific gravity diesel fuel at 60o F Step 1. Total equivalent length of fittings.
Step 2. Total length of pipe and fittings.
Step 3. Total friction loss (Appendix C).
Step 4. Net head available.
Step 5. Suction pressure available (Appendix A).
|
This particular site and pipe layout provides sufficient suction pressure for station 1. Required suction pressure is 20 psi and available pressure from gravity is 47.90 psi. To prevent vapor pockets in a gravity line, the grade from the tanks to the pumping station need not be uniform but should be free of excessive humps, pockets, and sharp bends.
(3) Flood Pumps. When gravity will not supply sufficient suction pressure for station 1, install a flood or suction pumping station as close to the tank-farm manifold as safety conditions permit. See Chapter 2 for operating characteristics on pump units.
b. Pumping Station 2. The location of pumping station 2 by use of the hydraulic gradient triangle depends on the positive suction pressure at station 1. Station 2 will maintain the minimum suction pressure that is to be passed along to each succeeding station on the pipeline. This pressure is 20 psi at normal elevations and temperatures.
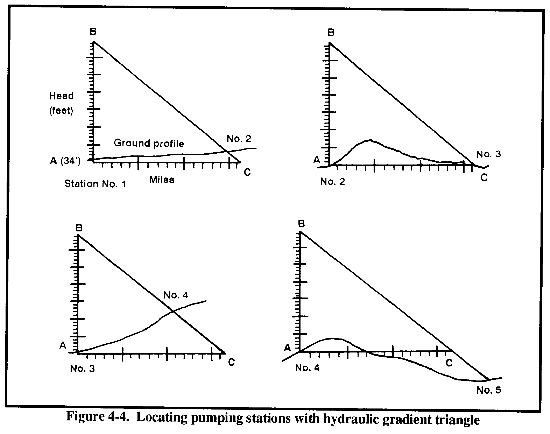
When suction pressure at station 1 is 20 psi, station 2 is easily located. Place the hydraulic gradient triangle on the pipeline profile with point A (the right angle) at station 1. The base (AC) of the triangle is positioned parallel to the horizontal baseline of the profile in the direction of flow in the pipeline. The point at which the hypotenuse of hydraulic gradient line (BC) intersects the profile is the proper location for station 2. The pressure at this point will be 20 psi, the same as the suction pressure at station 1. The triangle has measured the pumping distance for only the pressure added by the pumps at station 1, and the suction pressure does not have any bearing. In other words, station 1 started with a suction pressure of 20 psi.
c. Stations on Equal Elevations. If the pipeline profile does not intersect the hypotenuse of the hydraulic gradient triangle, the distance between two successive pumping stations on equal elevation is determined simply by the pressure drop due to pipeline friction. Hills and valleys along the route cancel each other out, and there is no loss of pressure due to changes in elevation.
For example, suppose that station 3 is at the same elevation as station 2. You would locate station 3 by placing point A of the hydraulic gradient triangle on the point fixed as station 2 on the profile. The base extends in the direction of flow and parallel to the baseline of the profile. If the two stations are actually on equal elevation, station 3 will be located where Point C of the triangle lies on the pipeline profile (see Figure 4-4).
d. Stations on an Upgrade. A downstream pumping station that is at a higher elevation than the preceding station is said to be on an upgrade. The total pressure loss between the two stations equals the sum of the separate losses due to friction and the difference in elevation. Logically, the downstream upgrade station will be closer to the preceding station than a downstream station at an equal elevation.
Suppose, because of the terrain, that station 4 is at a higher elevation than station 3. To locate station 4, place point A of the hydraulic gradient triangle on the point representing station 3 on the profile, with the base extending in the direction of flow and parallel to the baseline of the profile. The first point at which the hypotenuse or hydraulic gradient of the triangle intersects the profile is the appropriate location for station 4 (Figure 4-4).
e. Stations on a Downgrade. A downstream pumping station that is at a lower elevation than the preceding station is said to be on a downgrade. The pressure loss between stations will amount to the difference between the friction loss in the pipe. The pressure gain (static head) is due to the lower elevation of the downstream pumping station. A downstream station at a lower elevation than the preceding station will be farther from that station than it would be if both stations were at an equal elevation.
Suppose that pumping station 5 (downstream) is at a lower elevation than station 4 (upstream). To locate station 5, place point A of the hydraulic gradient triangle on the point that represents station 4 on the pipeline profile, with the base extending in the direction of flow and parallel to the baseline of the profile. Extend the hypotenuse (BC) until it crosses the profile of the pipeline. The point where BC intersects the profile is the proper location for station 5 (Figure 4-4).
f. Pressure-Reducing Stations. When pumping is interrupted and the pipeline is shut down, fluid in the line exerts static pressure between points of unequal elevation. Since there is no counteracting friction loss from fuel flow to use up or offset the static head, the total static pressure caused by the elevation difference is exerted against the pipe and the valve, which stops the flow. During normal flow, the safe working pressure of the pipeline may not be exceeded. During shutdown, the total static pressure applied may be well above the safe working pressure, especially at low sections in the line. To prevent this, place pressure-reducing stations on downgrades at all points where static pressure may become excessive.
To determine where to install a pressure reducing station in the line, construct a feet-of-head scale, similar to the line AB of the hydraulic gradient triangle in Figure 4-3, equal to the safe working pressure of the pipe being used. Be sure to use the same vertical scale as the pipeline profile. With the scale, measure downward from the highest elevation on the profile; at its base, project a horizontal line in the direction of the downgrade. The point where this horizontal line intersects the profile is the proper location of the pressure-reducing station (see Figure 4-5). For example, the safe working pressure for 6.247 ID aluminum pipe (Table 4-2) is 740 psi, which equals 2,011 feet of head for 0.85 specific gravity fuel by using the conversion factor in Appendix C.
The following methods are used to regulate static pressure in long downhill sections of military pipeline. Conditions, availability of materials and equipment, or other considerations will dictate which method you should use to protect the line when static pressure exceeds the capability of the pipeline tubing.
(1) Pressure-Reducing Valves. These valves will reduce upstream pressure about 25 to 800 psi and require no special tools to install. If these valves are available, using them is the best and easiest method of controlling excessive pressure.
(2) Heavier-Weight Pipe. When the higher safe working pressures of standard pipe can withstand static pressure, replace the lighter pipes on long downhill sections with heavier pipes to control the increased pressure exerted during shutdown. For example, the safe working pressure for 6-inch (0.219-inch wall thickness), standard-weight pipe is 1,000 psi. For 0.85 specific gravity fuel, the equivalent feet-of-head is 2,506 feet. In this example, replace the lightweight pipe with standard-weight pipe below the elevation in which the pipe strength is exceeded by static pressure.
g. Field Location of Pumping Stations. After the hydraulic locations of the pumping stations have been plotted on the profile of the pipeline (Figure 4-4), a site reconnaissance is made and the locations are plotted on topographic maps. The exact sites are located by measuring distances from easily identified landmarks or terrain features.
The pumping-station locations selected using the hydraulic-gradient-triangle method may not be suitable for many reasons. The locations may be inaccessible, difficult to camouflage, or too small; they may have poor vapor drainage or involve other unsuitable terrain conditions. If this occurs, the pumping station should be shifted upstream or downstream to a better site on the pipeline. Remember that a change in location also will change the suction and discharge pressures of the pumping station.
(1) Relocation Upstream. If a station must be relocated upstream, the available discharge head is equal to the normal discharge head plus the head from friction and elevation gained between the new location and the original location. Pressure conditions at the design rate of flow at the new pumping-station location must be reviewed to determine if discharge pressure of the preceding pump will exceed the maximum working pressure of the pipeline. If a station is relocated upstream, the next upstream station is relocated also so as to restore the proper 20-psi suction pressure.
(2) Relocation Downstream. Pumping stations may be shifted a short distance downstream on the pipeline to take advantage of good sites. However, the suction pressure at the relocated station cannot fall below 20 psi. The proper suction pressure must be restored at the succeeding pumping station. Relocation upstream is the best choice because the only effect on operations is an increase in suction pressure over the normal 20 psi. Relocation downstream without reduction of throughput can only be done by sacrificing part of the suction pressure. This should not be done unless minimum suction pressure can be maintained.
h. Poor Locations for Pumping Stations. A pumping station in a poor location either cannot pump at the required flow rate or it can pump at the required rate but with less than normal pressure. If a station fails to maintain flow at normal pressures, you can loop the line, or you can use larger pipe for a suitable distance on the downstream side of the pumping station to reduce friction loss by an amount that will permit it to pump at the design rate.
If a station does not have to pump under full pressure to pump at the required rate, it may be operated with fewer than the required number of pumping units. Or, when the station has to use only 50 percent or less of normal pressure (or lower RPM throttled back), the line may be looped around the next upstream station, which can then be eliminated from the line.
4-4. Treatment of Unusually Steep Grades. With unusually steep grades, it is possible that the safe working pressure of the pipe may be exceeded by dynamic head under normal design flow conditions.
|
Problem and Solution #6 The design flow is 550 GPM of 0.85 specific gravity fuel. The equipment used is 6.249 Id aluminum pipe and a 1,800-foot head-capacity pump. To determine whether the safe working pressure has been exceeded, compare the true hydraulic gradient triangle with the pipeline profile. Step 1. Draw the true hydraulic gradient (Figure 4-6, Step 1) by placing the hydraulic gradient triangle on the profile of the last located pumping station. Point A should be on the pumping-station location; the base should extend in the flow direction and parallel to the baseline of the profile to point C. Add the suction pressure that is passed on form station to station by extending the available head scale form point B to B1, a distance equal to that suction head pressure or 54 feet (0.85 specific gravity fuel at 20 psi). From this point B1, draw a line on the profile parallel to the hypotenuse of the hydraulic triangle. This line, B1 to C1, is the true hydraulic gradient at design flow. Step 2. On a stiff piece of cardboard or clear plastic make a feet-of-head scale corresponding to the safe working pressure of the pipeline. Label this scale D to E (see Figure 4-6, Step 1) The equivalent feet-of-head for 6.249-ID aluminum pipe at 0.85 specific gravity with a safe working pressure of 740 psi is 2,011 feet. Move this scale along the hypotenuse of the true gradient triangle with the point E on the true hydraulic gradient and the scale perpendicular to the baseline of the profile. Mark the point on the pipeline profile P1. Continue moving the scale along the true hydraulic gradient hypotenuse, and mark the profile at the point at which the bottom edge of the scale again passes through the profile P2. Step 3. The section of the pipeline between points P1 and P2 will build up dynamic pressure exceeding the safe working limits of the aluminum pipe used under design-flow conditions. For this critical section, redesign the line. You can redesign by replacing the aluminum coupled pipe in the high-pressure segment of line with standard welded pipe. The following effects will result:
Step 4. Make a new hydraulic gradient triangle for the standard pipe using the same scale as the pipeline profile. The altitude is 1,800 feet or the available head capacity of the pump unit. The base is figured by dividing the available head capacity of the pumping unit by the line loss per mile based on design flow. In this example, the pump capacity is 1,800 feet of head, and the design flow capacity is 550 GPM. The friction head loss for standard pipe (0.219-inch wall thickness) is 90 feet per mile. Calculate the base by dividing 1,800 feet of head by 90 feet of head loss per mile. The result is 20 miles. Use the same scale to construct a new hydraulic gradient triangle. Place the new hydraulic gradient triangle, based on standard pipe (Figure 4-6, Step 2), with point B2 on the true gradient parallel to the baseline of the profile. With the triangle in this position, draw the new hydraulic gradient on the profile. Step 5. Conduct a test to determine if the safe working pressure of the standard pipe is exceeded at any point. Construct a feet-of head scale for standard pipe as in Step 2 above. See Table 4-2 for dimensions and safe working pressures for standard pipe supplied in pipeline assemblies. In Figure 4-6, Step 2 the scale F to G is the safe-working-pressure scale for 6-inch standard pipe (0.0.219-inch wall thickness). For this pipe, the maximum safe working pressure is 1,500 psi, which is equivalent to 3,759 feet-of-head of 0.85 specific gravity fuel. Step 6. Check the vertical distances between the new hydraulic gradient and the pipeline profile as in Step 2 above. If the bottom edge of the feet-of-head scale does not pass above the pipeline profile at any point, the safe working pressure of the standard pipe is not exceeded. Using the feet-to-head scale for the aluminum pipe (D to E), prepared according to Step 2 above, locate the point on the profile where the pressure drops below the safe working pressure of the aluminum pipe tubing by moving the scale along the new hydraulic gradient based on standard pipe. The point (P3) at which the bottom edge of the scale first passes below the profile is the transition point where aluminum pipe may be used again in the pipeline. Step 7. Locate the next pumping station (Figure 4-6, Step 3) using the original hydraulic gradient triangle. Position the feet-of-head scale directly above the transition point between standard pipe and aluminum pipe (P3). Add the suction head pressure required at each pumping station (20 psi or 54 feet) to the feet-of head scale, which is the same as B1 in Step 1 above. Position point B1 of the triangle on the new hydraulic gradient. This procedure restores the standard pumping-station suction pressure. Draw a line parallel to the original true hydraulic gradient unit it intersects the pipeline profile. The point where this line intersects the pipeline profile is the proper location for the next pumping station. |
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|