Chapter 7
Neutron-Induced Radiation Areas
As discussed in the beginning of Chapter 3, neutrons are produced in all nuclear weapon bursts. Some of these neutrons may be captured by the various elements in the soil under the burst. As a result, these elements become radioactive, emitting beta particles and gamma radiation for an extended period.
Beta particles are a negligible hazard unless the radioactive material makes direct contact with the skin for an extended period or is inhaled. Beta particles can cause skin irritations varying from reddening to open sores. In contrast, gamma radiation readily penetrates the body and can cause radiation injury and even death. To determine the external military hazard posed by induced radiation, an analysis of the dose rate of the emitted gamma radiation must be determined. For this reason neutron-induced areas are considered areas of gamma activity.
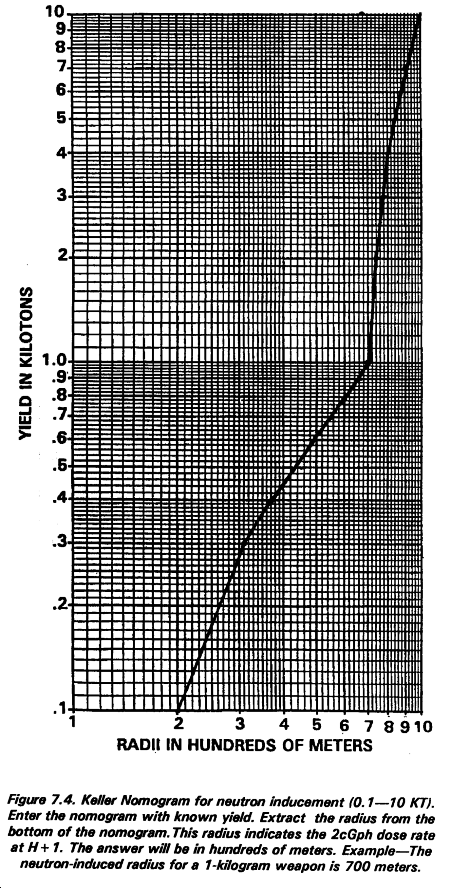
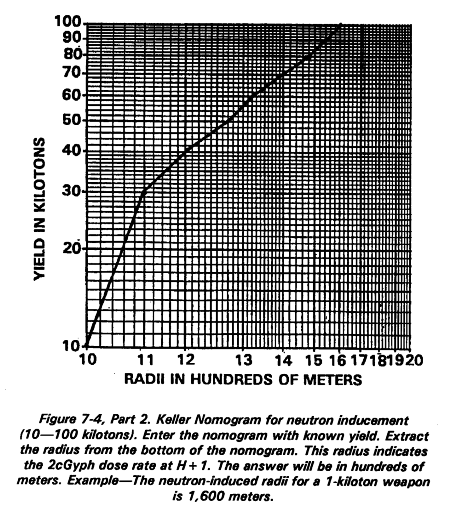
The location of a suspected induced-radiation area created by an airburst is determined by nuclear burst data. Weather conditions have no influence upon its location or size. Surface winds will not affect the pattern. The pattern, if produced, will always be around GZ. The size of the pattern depends on the yield of the weapon and the height of burst. Figure 7-1 shows the boundaries of the induced area for different yields. Refer to Figure 7-4 for the Keller Nomogram. Assuming an optimum height of the weapon (or interpolated if not listed), the distance given is the maximuim horizontal radius to which a 2-cGyph dose rate will extend one hour after burst.
On the map overlay, this radius is drawn about the GZ point as a circle. The circle is labeled, and nuclear burst data and overlay data are recorded. (See Figure 7-2.) This area is regarded as contaminated until actual dose-rate readings indicate otherwise. The actual area of contamination is usually substantially less, depending upon actual yield and height of burst.
Avoid neutron-induced radiation areas whenever possible. If the area cannot be avoided, the commander must follow the protection techniques for fallout.
To avoid neutron-induced radiation, the commander must know where the suspected area may be. All enemy airbursts are assumed to create hazard areas. Friendly bursts employed in packages may create induced areas very near one another. Commanders must understand that the GZ for an airburst should not be crossed for 24 to 96 hours after the burst. Routine occupancy of an area of induced radiation is possible from two to five days after burst. In this case, low dose rates become even more significant. This is because of the accumulated dose acquired over the period of exposure. A commander should seek the least contaminated region available. During occupancy, the area should be checked with the dosimeter once an hour.
Plotting NIGA Areas
To plot a neutron-induced gamma activity area, enter Figure 7-4, Part 1 or Part 2, with the known yield on the left side of the chart. Lay the hairline across the chart and pin down the hairline on the dark black index line. Rotate the hairline laterally and read the radii of the NIGA pattern in hundreds of meters at the bottom of the chart.
Decay of Induced Radiation
The soil in the target area is radioactive to a depth of 0.5 meter at GZ. In contrast, fallout is a deposit of radioactive dust on the surface. From this it can be seen that decon of the induced-radiation area is impractical.
Decay characteristics of induced radiation are considerably different from those of fallout. Fallout is a mixture of many substances, all with different rates of decay. Induced radiation is produced primarily in aluminum, manganese, and sodium. Other elements, such as silicon, emit so little gamma radiation, or decay so fast, that they are less important. During the first 30 minutes after a burst, the principal contributor to induced radiation is radioactive aluminum.
Almost all soils contain aluminum. It is one of the most abundant elements in the earth's surface. Aluminum-28 has a half-life of 2.3 minutes. Because of this, almost all of the radioactive aluminum has decayed within 30 minutes after burst.
Most soils also contain significant quantities of manganese. This element, Manganese 56 has a half-life of 2.6 hours. From 30 minutes after burst until 10 to 20 hours after burst, both manganese and Sodium 24, which has a half-life of 15 hours are the principal contributors to radiation. After 10 to 20 hours after burst, Sodium 24, is the principal source of radiation.
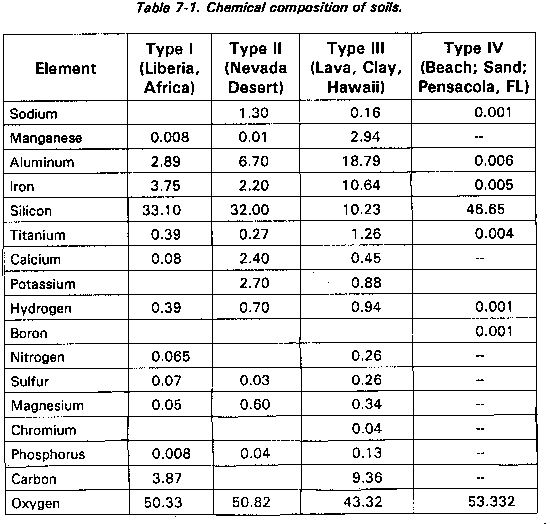
Soil composition is the most important factor in the decay of induced radiation. Its decay must be considered differently from that of fallout. For fallout, the decay rate is calculated by using the Kaufman equation. For induced radiation, the percentage, by weight, of elements present in the soil determines the decay rate. Since soil composition varies widely, even in a localized area, you must know the actual chemical composition of the soil to determine the rate of decay of induced radiation.
All soils are divided into four types. Table 7-1 has been extracted from Defense Nuclear Agency Effects Manual 1 (DNA E-M-1). Since the actual soil composition will not be known, Soil Type II, the slowest decay, is used for all calculations until the NBCC advises use of a different soil type.
Soil type is determined by using engineer soil maps or an NBC 4 report and the induced-decay nomograms. The method is basically a process of elimination. The dose rate and the time it was measured are applied to an induced-decay nomogram. This results in an H + 1 or R1 dose rate. Then, if the other dose rates and times from the series report result in the same R1 dose rate, that is the soil type. If not, check the other nomograms until the one used results in the same R1.
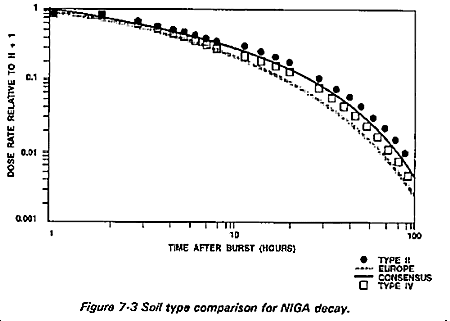
Soil Type II is listed as the type of soil found in the Nevada Desert. This is due to the amount of sodium and manganese in the soil and not the composition as a whole. Figure 7-3 depicits a graph comparing NIGA decay for various soils. From this graph, Soil Type II NIGA decay compares directly to the soil type labeled Consensus. Consensus is the average soil (sodium and manganese content only) world-wide. Therefore, Soil Type II is considered the standard soil used for calculations when the actual soil type is unknown.
From Figure 7-3, Soil Type IV compares directly to the average European soil, in sodium and manganese content. Therefore, use Soil Type IV when determining NIGA decay in this region.
Dose-Rate Calculations
The decrease in the dose rate must be calculated before total dose can be found. This is done with decay nomograms. Use the residual radiation (induced) decay nomograms in Appendix E (Figures E-44, E-45, E-48 and E49) for these calculations. They allow the user to predict the dose rate at any time after the burst. Each nomogram denotes time (hours) after burst for one of the four soil types.
In each nomogram, the R1 scale is at the right. This scale shows H + 1 dose rates. The Rt scale is on the left. This scale shows dose rates at times other than H + 1.
In working with nomograms, be as consistent as possible when joining values with the hairline. Be sure the hairline intersects the vertical line and the interpolated value (tick mark) as closely as possible. The following three problems are concerned with technique only; they do not consider the impact that high dose rates might have on operations in the contaminated area. Each problem requires the use of a Keller nomogram for solving the problem (Figure 7-4, parts 1 and 2). The caption for each nomogram contains a guide for using the nomogram.
Problem 1.
Given: Rt = 150 cGyph at H + 3 hours, Soil Type II.
Find: R1.
Answer: 180 cGyph.
Solution: Select nomogram for Soil Type II. Align the hairline with the 3-hour tick mark on the Time (middle) scale (t) and the 150 cGyph point on the Rt scale. Read the dose rate as 180 cGyph at the point of intersection with the R1 scale.
Problem 2.
Given: R1 = 300 cGyph, Soil Type III.
Find: Rt at H + 7 hours.
Answer: 63 cGyph.
Solution: Select nomogram for Soil Type III. Align the hairline with the 7-hour tick mark on the Time (middle) scale (t) and the 300-cGyph point on the R1 scale. Read the dose rate as 63 cGyph at the point of intersection with the Rt scale.
Problem 3.
Given: R1 = 200 cGyph, Soil Type IV.
Find: time (t) when Rt = 70 cGyph.
Answer: H + 11 hours.
Solution: Select nomogram for Soil Type IV. Align the hairline with 200 cGyph on the R1 scale and 70 cGyph on the Rt scale. Read the time as H + 11 hours at the point of intersection of the hairline with the time scale.
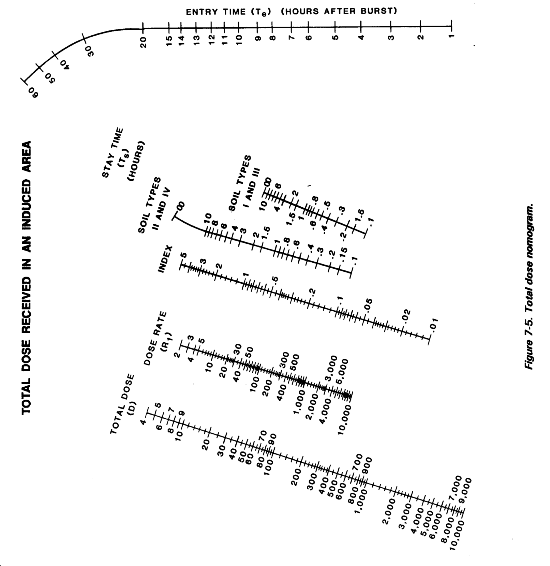
Total Dose Calculations for NIGA
Use the nomogram in Figure 7-5 for predicting the total dose received in an induced area. This nomogram relates total dose, H + 1 dose rate, stay time, and entry time. The two scales to the left of the index line show total dose and H + 1 dose rate. There are two time-of-stay scales to the right of the index line. The extreme right scale shows time of entry. The index line is a "pivoting" line used as an intermediate step between D and R1. R1 is found by using one of the induced decay nomograms. If soil type is unknown, assume the soil is type II. The total dose nomogram, Figure 7-5 is never used to find R1.
In Figure 7-5, soil types II and IV under stay time are used for total dose calculations if the soil type is not known. If the soil type is known, the appropriate scale under stay time is used. It is possible to find any one value on the total dose nomogram if the other three are given, as illustrated in the following problems.
These problems are concerned with techniques only. They do not consider the impact the dose or dose rates might have on operations in a contaminated area.
Problem 1.
Given: R1 = 140 cGyph
Te = H + 6 hours
Ts = 1 hour
Soil Type II.
Find: D.
Answer: 72 cGy.
Solution: On the nomogram in Figure 7-5, connect H + 6 on the Te scale with 1 hour on the Ts scale (soil types II and IV) with a hairline. Pin the hairline at the point of intersection with the index scale. Now pivot the hairline to 140 cGyph on the R1 scale. Read 72 cGy on the D scale.
Problem 2.
Given: R1 = 300 cGyph
Te = H + 6 hours
D = 70 cGy
Soil Type III.
Find: Ts.
Answer: 1 hour.
Solution: On nomogram in Figure 7-5, connect 70 cGy on the D scale with 300 cGyph on the R1 scale. Pin the hairline at the point of intersection with the index scale. Pivot the hairline to H + 6 hours on the Te. scale. Read 1 hour on the Ts scale (soil types I and III).
Crossing an Induced-Radiation Area
If an area must be crossed, select the lowest dose rate area, consistent with the mission. Route selection may be influenced by several factors. Unpassable terrain, such as mountains or swamps, may influence the route. Obstacles, such as tree blowdown, fires, or rubble, also may limit the number of routes or the mode of movement.
If an option exists for crossing an induced area, select the method in the following priority order:
1. Aircraft.
2. Armored vehicles and personnel carriers.
3. Wheeled vehicles.
4. On foot.
Sandbag all vehicles used in crossing to increase shielding. Sandbag floors and sides of cargo vehicles. APCs should be sandbagged both on top and bottom. Always use uncontaminated soil in the sandbags.
As with fallout, the limit to the amount of exposure to radiation is expressed by the higher commander's OEG. To meet this OEG, the lower commander must employ as many of the dose reduction principles as possible.
In calculating total dose, it is necessary to determine an average dose rate. Dose rates increase as the center of the area is approached, and then decrease beyond the center of the area. The average dose rate represents a mean value the individual is exposed to during the time of stay. A reasonable approximation of the average dose rate can be obtained by dividing by two the maximum dose rate

Time of stay: Time of stay (stay time) must be calculated for crossing problems. Use the folowing relationship:
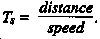
Problem.
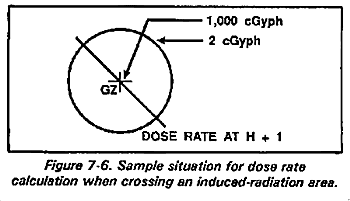
Figure 7-6 shows an example problem for calculating dose when crossing an induced radiation area.
Given: A crossing will take place (as shown in Figure 7-6) at H + 20 hours. Distance of the route across the area is 1 kilometer. Speed during the crossing (on foot) will be 5 kilometers per hour.
Find: D.
Answer: 20 cGy.
Solution:
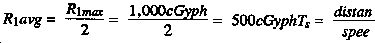
Te = H + 20 hours.
On the nomogram in Figure 7-5, connect 0.2 hours on the Ts scale (soil types II and IV) and 20 hours on the Te scale with a hairline. Pivot through the point of intersection with the index scale to 500 cGyph on the R1 scale. Read a total dose of 19 cGy on the D scale at the point of intersection with the hairline.
Problem 2.
Given: An induced area with Soil Type II must be crossed at H + 10 hours. Distance across the area is 1 kilometer. Speed of crossing is 10 kilometers per hour. The highest H + 1 dose rate is 300 cGyph. Crossing will be conducted in APCs with a TF of 0.22.
Find: ID.
Answer: 1.32 cGy, or 1 cGy.
Solution:
1. Calculate R1 avg:

3. On the nomogram in Figure 7-5, connect 10 hours on the Te scale with 0.1 hour on the Ts scale (soil types II and IV). Pin the hairline on the index scale. Pivot the hairline 150 cGyph on the R1 scale. Read the outside dose as 6 cGy.
4. Calculate the inside total dose:
inside dose = outside dose x TF
= 6 cGy x 0.22
= 1.32 cGy, or 1 cGy.
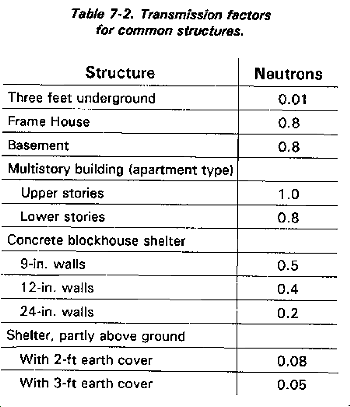
Transmission Factors for Neutron-Induced Areas
Transmission factors for induced areas are determined in the field. The TFs in Table 7-2 should be used with the greatest reservation. Actual TFs in induced areas may be higher by as much as 70 percent, because of a very technical characteristic of radiation. Essentially the strength of gamma radiation is measured in million electron volts (MEV). Fallout less than 24 hours old has an average energy of 0.67 MEV. Induced radiation emitted from the three principal soil elements has a range of 0.68 MEV to 1.2 MEV.
Because of the unique decay characteristics of induced radiation, TFs must be recalculated frequently. Every four hours is recommended. This accounts for changes in the penetrating ability of the remaining radiation.
Field calculation of neutron-induced TFs is identical to that for fallout. TFs may be applied to dose rates or total dose.
The following mathematical calculations relate to NIGA from a single burst at a single location.
Determination of Decay Rate for Induced Radiation
Decay characteristics of induced radiation are considerably different from those of fallout. The Kaufman equation may not be applied.
The decay of induced radiation depends on the elements in which it is induced. Soil contains many different elements with varying half-lives, so, the decay rate changes in time, and must be monitored constantly.
The decay rate n at a fixed location can only be determined from consecutive measurements, using the following equation:
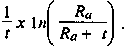
Ra is the dose rate reading in cGyph at an arbitrary time a and Ra + t is a second reading taken at the same location after t hours. One n () is the natural logarithm to base e (e = 2.71828..., Eulerian constant).
Manganese and sodium are two elements frequently found in soils with relatively long half-lives. Therefore, they are expected to be the principal sources of radiation after a burst. For sodium with its half-life of 15 hours, the decay rate is 0.046. For manganese with its half-life of 2.6 hours, the decay rate is 0.27.
Determination of the Dose Rate for an Arbitrary Time
The dose rate R1 + t in cGyph at an arbitrary time t hours after a reading is calculated as R1 + t = Ra * EXP ( -n * t ). Ra is the dose rate at the time t of the reading, n is the decay rate at that time, and exp () is the exponential function (inverse or INV (); the argument is the power to which e = 2.71828 . . . is raised).
Note: The following characters or character combinations indicate keys on the pocket calculator: *, EXP, Yx, INV, ( and ). When you encounter one of these in a formula, press the key indicated. Remember that negative n (-n) is not an indication to press the minus key.
Determination of Dose Accumulated in an NIGA Area
The dose D in cGy accumulated between entry to and exit from an NIGA area is found by using the formula--
D= R1/n* ( EXP (-n* Te ) - EXP ( -n* tout) ). R1 is the dose rate in cGyph at the reference time, n is the decay rate at that time, tin and tout are the time of entry and exit from the NIGA area in hours after the reference time. EXP () is the exponential function.
Determination of Time of Exit from an NIGA Area Given a Maximum Dosage
If a certain limit DL for the dose accumulated during a stay in an NIGA area is given, the time tout to leave the area can be determined from the following equation:
Tout = -l/n * 1n ( EXP ( -n* Te ) - ( n * DL ) / Rl.
Where Te is the time of entry in hours after the reference time at which the dose rate was R1 and the decay rate was D. One n () and EXP() are the natural logarithm and the exponential function, respectively.Determination of the Earliest Time of Entry. To ensure a limiting dose DL is not accumulated during a stay in an NIGA area, the earliest time of entry tin can be determined as follows:
Te = -1/n* ( DL / ( R * n * ( l - exp( -n * Ts ) ) ) ).
Where Ts is the time of stay in the area in hours, Rr is the dose rate at the reference time H + 1, and n is the decay rate at that time. One n () and EXP () are the natural logarithm and the exponential function, respectively.There are two other methods to calculate crossing problems. The hand-held pocket calculator method:
Step 1. Turn on the calculator, and punch in the value for Rl, press "÷"; then "( 1 - n )."
Step 2. Press the multiplication key; then "(" and the value for Ts. Then push the power key "Yx."
Step 3. Press "(" again and 1 - n. push the minus symbol "-."
Step 4. Again, press "(", the value for Te, and "Yx." Press "(" again and then "1 - n." Press "(" twice, then equals.
The whole equation written out looks like this--
D = R1 ¸ (1 - n ) x (Ts Yx ( l - n ) - ( Te Yx (l - n ) ) ) =.
For time of entry (Te)--
Te = Ts Yx (1 - n ) - D x ( l - n ) ÷ R1 = INV Yx ( 1 - n ) =.
For time of stay (Ts)--
Ts =D x ( l - n ) ÷ R1 +Te ,Yx ( l - n ) = INV Yx ( 1 - n )=.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|