Radar Cross Section (RCS)
The units of radar cross section are square meters; however, the radar cross section is NOT the same as the area of the target. Because of the wide range of amplitudes typically encountered on a target, RCS is frequently expressed in dBsm, or decibels relative to one square meter. The RCS is the projected area of a metal sphere that is large compared with the wavelength and that, if substituted for the object, would scatter identically the same power back to the radar. However, the RCS of all but the simplest scatterers fluctuates greatly with the orientation of the object, so the notion of an equivalent sphere is not very useful.
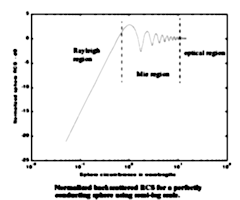
Different structures will exhibit different RCS dependence on frequency than a sphere. However, three frequency regimes are identifiable for most structures. In the Rayleigh region at low frequencies, target dimensions are much less than the radar wavelength. In this region RCS is proportional with the fourth power of the frequency. In the Resonance or Mie Region at medium frequencies, target dimensions and the radar wavelength are in the same order. The RCS oscillates in the resonance region. In the Optical Region of high frequencies, target dimensions are very large compared to the radar wavelength. In this region RCS is roughly the same size as the real area of target. The RCS behaves more simply in the high-frequency region. In this region, the RCS of a sphere is constant.
In general, codes based on the methods-of-moments (MOM) solution to the electrical field integral equation (EFIE) are used to calculate scattering in the Rayleigh and resonance regions. Codes based on physical optics (PO) and the physical theory of diffraction (PTD) are used in the optical or high-frequency region. The target's electrical size (which is proportional to frequency and inversely proportional to the radar wavelength) that determines the appropriate algorithm to calculate the scattering. When the target length is less than 5 to 10 wavelengths, the EFIE-MOM algorithm is used. Alternatively, if the target wavelength is above 5 to 10 wavelengths, the PO-PTD algorithm is used.
The RCS of a stealth aircraft is typically multiple orders of magnitude lower than a conventional plane and is often comparable to that of a small bird or large insect. "From the front, the F/A-22's signature is -40dBm2 (the size of a marble) while the F-35's is -30 dBm2 (the size of a golf ball). The F-35 is said to have a small area of vulnerability from the rear because engineers reduced cost by not designing a radar blocker for the engine exhaust." [Aviation Week & Space Technology; 11/14/2005, page 27] The F-35 stealthiness is a bit better than the B-2 bomber, which, in turn, was twice as good as that on the even older F-117. B-2 stealth bomber has a very small cross section. The RCS of a B-26 bomber exceeds 35 dBm2 (3100m2 ) from certain angles. In contrast, the RCS of the B-2 stealth bomber is widely reported to be about -40dBm2 .
A conventional fighter aircraft such as an F-4 has an RCS of about six square meters (m2), and the much larger but low-observable B-2 bomber, which incorporates advanced stealth technologies into its design, by some accounts has an RCS of approximately 0.75 m2 [this is four orders of magintude greater than the widely reported -40dBm2 ]. Some reports give the B-2 a head-on radar cross section no larger than a bird, 0.01 m2 or -20dBm2. A typical cruise missile with UAV-like characteristics has an RCS in the range of 1 m2; the Tomahawk ALCM, designed in the 1970s and utilizing the fairly simple low-observable technologies then available, has an RCS of less than 0.05 m2.
The impact of lowered observability can be dramatic because it reduces the maximum detection range from missile defenses, resulting in minimal time for intercept. The US airborne warning and control system (AWACS) radar system was designed to detect aircraft with an RCS of 7 m2 at a range of at least 370 km and typical nonstealthy cruise missiles at a range of at least 227 km; stealthy cruise missiles, however, could approach air defenses to within 108 km before being detected. If such missiles traveled at a speed of 805 km per hour (500 miles per hour), air defenses would have only eight minutes to engage and destroy the stealthy missile and 17 minutes for the nonstealthy missile. Furthermore, a low-observable LACM can be difficult to engage and destroy, even if detected. Cruise missiles with an RCS of 0.1 m2 or smaller are difficult for surface-to-air missile (SAM) fire-control radars to track. Consequently, even if a SAM battery detects the missile, it may not acquire a sufficient lock on the target to complete the intercept.
Radar scattering from any realistic target is a function of the body's material properties as well as its geometry. Once the specular reflections have been eliminated by radar absorbing materials, only nonspecular or diffractive sources are left. Non-specular scatterers are edges, creeping waves, and traveling waves. They often dominate backscattering patterns of realistic targets in the aspect ranges of most interest. The traveling wave is a high frequency phenomenon. Surface traveling waves are launched for horizontal polarization and grazing angles of incidence on targets with longs mooth surfaces. There is little attenuation from the flat smooth surface, so the wave builds up as it travels along the target. Upon reaching a surface discontinuity, for example an edge, the traveling wave is scattered and part of it propagates back toward the radar. The sum of the traveling waves propagating from the far end of the target toward the near end is the dominant source to the target radar cross section.
The radar cross section (RCS) of a target not only depends on the physical shape and its composite materials, but also on its subcomponents such as antennas and other sensors. These components on the platforms may be designed to meet low RCS requirements as well as their sensor system requirements. In some cases, the onboard sensors can be the predominant factor in determining a platform's total RCS. A typical example is a reciprocal high gain antenna on a low RCS platform. If the antenna beam is pointed toward the radarand the radar frequency is in the antenna operating band, theantenna scattering can be significant.
The traditional measure of an object's scattering behavior is the RCS pattern which plots the scattered field magnitude as a function of aspect angle for a particular frequency and polarization. Although suitable to calculate the power received by a radar operating with those particular parameters, the RCS pattern is an incomplete descriptor of the object's scattering behavior. While the RCS pattern indicates the effect of the scattering mechanism, it does not reveal the physical processes which cause the observed effect. In contrast, imaging techniques, which exploit frequency and angle diversity to spatially resolve the reflectivity distribution of complex objects, allow the association of physical features with scattering mechanisms. These processes, therefore, indicate the causal components of the overall signature level observed in RCS patterns.
| Target | RCS (m2) | References |
|---|---|---|
| Navy cruiser (length 200m) | 14000 | [5] |
| B-52 Stratofortress | 100 125 | [1], [5], [6] |
| C-130 Hercules | 80 | [5] |
| F-15 Eagle | 1025 | [7], [8] |
| Su-27 Flanker | 1015 | [7], [8] |
| F-4 Phantom | 610 | [1], [5] |
| Mig-29 Fulcrum | 35 | [1], [7], [8] |
| F-16A | 5 | |
| F-18 C/D Hornet | 13 | [6], [7] |
| M-2000 | 12 | [7], [8] |
| F-16 C (with reduced RCS) | 1.2 | [6] |
| T-38 Talon | 1 | [5] |
| B-1B Lancer | 0.751 | [1], [5] |
| Sukhoi FGFA prototype | 0.5 | [9] |
| Tomahawk TLAM | 0.5 | |
| Exocet, Harpoon | 0.1 | [6] |
| Eurofighter Typhoon | 0.1 class | [6], [7], [8] |
| F-18 E/F Super Hornet | 0.1 class | [6], [7], [8] |
| F-16 IN Super Viper | 0.1 class | [2] |
| Rafale | 0.1 class | [1], [2], [6], [7], [8] |
| B-2 Spirit | 0.1 or less | [1], [6] |
| F-117A Nighthawk | 0.025 or less | [1], [6] |
| bird | 0.01 | [3] |
| F-35 Lightning II | 0.0015 0,005 | [6], [7], [8] |
| F-22 Raptor | 0,00010.0005 | [6], [7], [8] |
| insect | 0.00001 | [3] |
SOURCE : Low Observable Principles, Stealth Aircraft and Anti-Stealth Technologies Konstantinos Zikidis, Alexios Skondras, Charisios Tokas, December 2013
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|