APPENDIX E
ROAD MOVEMENT PLANNING
E-1. INTRODUCTION. A movement graph is a method of graphically portraying movements along a single route. It shows the relationship between time and distance and highlights any conflicts between columns scheduled for movement on the route. Movement planners can use movement graphs during planning when conflicts are anticipated or when restrictions are applied to routes.
This appendix is divided into four sections. Section I outlines fundamentals of graphing, route restrictions, and movement tables. Section II shows planning factors for highway movement. Section III describes the graphing, managing, and preparing of movement tables for a highway movement. Section IV outlines how to manage movements over multiple routes using a critical time and point graph.
Section I. Graphing
E-2. PREPARING A GRAPH. Movement graphs can be prepared on any type of graph paper. The vertical axis shows distance and the horizontal axis shows time. The lower left corner of the graph represents zero kilometers (or miles) and the earliest start time of the movement. The planner creating the graph must apply a scale to the vertical and horizontal axis as shown in Figure E-1.
The scale of the vertical axis is a division of the total distance. The top number on the vertical axis is the greatest number of km (or miles) to be traveled by any element on the route. The distance scale shown in Figure E-1 is 3 km per block.
The scale of the horizontal axis is a division of the total time. The time at the end of the horizontal scale shows the latest planning time to complete all movements planned for the route. The time scale shown in Figure E-1 is 12 minutes per block.
Critical points along the route, such as built up areas, road junctions, and CPs are shown along the vertical axis on the same scale as that of the graph. The SP and RP can also be annotated alongside the CP if all movements begin and end at the same CP.
The graph at Figure E-1 shows the time and distance scales, critical points, CPs, and a plotted line representing the movement of one vehicle (or the first vehicle of a column) from the SP (Newport) to Jackson Heights. Based on the scale of each block representing 3 km and 12 minutes, the head of the convoy will leave Newport at 0400, travel 90 km to Jackson Heights, and arrive at 0700. Using the formula to determine march rate (R = D ¸ T) the march rate is 30 kmph.
Figure E-1. Schedule of Head of Column
March columns, serials, and march units are represented on a graph by parallel diagonal lines like the ones shown in Figure E-2. The vertical space between the diagonal lines is the length of roadway (length) occupied by the column. It is measured along the vertical scale. The horizontal space is the time it takes for the column to pass any given point (pass time or time length).
The head of the column is plotted at the intersection of the SP on the vertical scale and start time on the horizontal scale. The clear time of the head of the column is plotted at the intersection of the RP on the vertical scale and the clear time on the horizontal scale.
The trail of the column is plotted at the intersection of the same SP on the horizontal scale. The trail vehicle's start time is calculated by adding the pass time to the start time of the first vehicle. The clear time of the trail vehicle is plotted at the intersection of the RP on the vertical scale and its clear time on the horizontal scale. The trail vehicle's clear time is calculated by adding the pass time to the clear time of the first vehicle.
Figure E-2. March Graph Showing Movement of a Column
The graph now completely pictures the movement of one column. The vertical and horizontal scales reveal the following information:
- The two parallel diagonal lines show the head and the trail movements.
- The column's length is about 14 km.
- The pass time of the column is 36 minutes. That means that it will take 36 minutes for the column to clear any point along the route.
- The road distance from SP to RP is about 96 km. The time distance is 4 hours (0700 to 1100). That means it will take 4 hours for the head of the column to clear the RP.
- Road clearance time, calculated by adding the pass time to the time distance, is 4 hours and 36 minutes.
- Road clearance distance, calculated by adding the length to road distance, is 110 km.
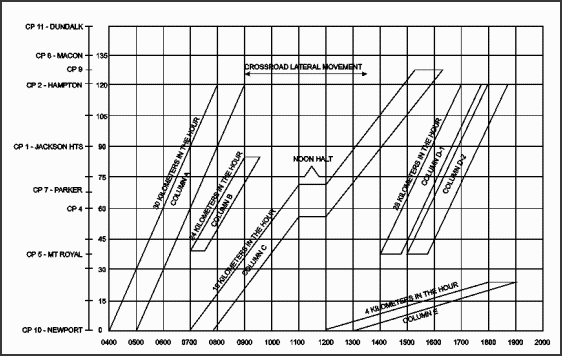
March graphs are normally used to show multiple columns traveling over the same routes as shown in Figure E-3. Each of these columns is explained below.
Figure E-3. Scheduling Moves
- Column A is scheduled to leave its SP (Newport) at 0400 and clear the SP at 0500, a pass time of 1 hour. Distance to the RP (Hampton) is 120 km. The rate of march is 30 kmih. The time distance is 4 hours (120 km ¸ 30 kmih). The head will arrive at the RP at 0800 and the trail at 0900. Therefore, the road clearance time is 5 hours, which is the time distance plus the pass time.
- Column B makes a shorter move at a different time. It is scheduled to leave its SP (Mount Royal) at 0700 and clear the CP at 0730, a pass time of 30 minutes. Distance to the RP is 48 km. The rate of march is 24 kmih. The time distance is 2 hours (48 ¸ 24 kmih). The head will arrive at the RP at 0900 and the trail at 0930. Therefore, the road clearance time is 2 1/2 hours. The graph shows that this move does not conflict with the first move.
NOTE: A crossroad lateral movement is scheduled to cross at CP 1 from 0906 until 1312. The graph shows that the lateral movement will not interfere with any of the scheduled moves.
- Column C makes a longer and slower move than the other columns. The graph shows this because the diagonal lines representing time distance are not as steep as the lines of columns A, B, and D. The steepness of a diagonal line on the graph indicates the rate of march. Column C is scheduled to leave its SP (Newport) at 0700 and clear the SP at 0750, a pass time of 50 minutes. Distance to the RP is 132 ¸ km. The rate of march is 18 kmih. Column C is also scheduled for a 1 hour rest halt on the road. Rest halt time is added to the time distance when calculating. Therefore, the time distance is 132 km ¸ 18 kmih + 1 hour or 8 hours and 20 minutes. The road clearance time is 9 hours and 10 minutes.
- Columns D-1 and D-2 are two serials of one column. They are scheduled to travel at 28 kmih from the same SP to the same RP, one leaving 24 minutes after the other. The graph shows that the head of Column D-1 is scheduled to leave the SP at 1400 and arrive at the RP at 1700, a distance of 84 km in 3 hours. The rate of march is 28 kmih (84 ¸ 3 hours). Because both elements of the move are shown on the graph parallel to each other, the rate is the same for both.
- Column E is a foot march on the route. It is traveling slowly (24 km in 6 hours of walking time).
E-3. PLANNING FOR ROUTE RESTRICTIONS. Planners must consider route restrictions when graphing movements. These restrictions normally add greater control measures to a route. They may be imposed to allow for route maintenance, large unit movements, or maneuver. They should be specified in highway regulation plans, OPORDs, or FRAGOs.
Restrictions are marked on graphs by blocking out the time and space on the graph when traffic may not use a route or cross an intersection. To plan around restrictions, planners can calculate either earliest or latest time a column can leave the SP to miss the restriction.
When passing after restriction ends, use the following formula. Compute the earliest time the head of the column can cross the SP to clear the ending time of a route restriction without halting at the restriction.
The earliest time the first vehicle can cross the SP = end of restriction time + safety factor - time distance from start point to restriction point.
EXAMPLE: A restriction is in effect from 1140 to 1240. The distance from the SP to the restriction is 32 km. A safety factor of 15 minutes is in force before and after the restriction. This is a close column move executed at the rate of 16 kmih. Pass time is 12 minutes. Using the formula, calculate the earliest time the first vehicle can cross the SP.
| 1240 + 15 min - | 32 km = 1255 - 2 hr = 1055 16 kmih |
The earliest time the column can leave the SP is 1055.
When passing before restriction begins, use the following formula. Compute the latest time the first vehicle of a column can cross the SP to have the last vehicle arrive at the 1140 to 1240 restriction before it begins.
The latest time the first vehicle of a column can cross the SP = beginning of restriction time - safety factor - time distance from SP to the restriction - time length. Using the data in the example above, calculate the time.
| 1140 - 15 min - | 32kmM - 12 min = 1125 - 2 hours - 12 min = 0913 16 kmih |
The latest time the first vehicle can leave the SP is 0913.
Section II. Highway Movement Planning Factors
E-4. MOVEMENT MEASUREMENT. Movements are measured by calculating how long it takes to move a given distance. The three methods of measurement are speed, pace, and rate of march. Movement planners normally use rate of march in performing movement calculations.
a. Speed. Speed is the actual rate at which a vehicle is moving at a given time as shown on the speedometer. It is expressed as kilometers or miles per hour (kmph or mph).
b. Pace. Pace is the regulated speed of a convoy or an element as set by a lead vehicle, the pacesetter. It is constantly adjusted to suit road, terrain, and weather conditions. Pace is also expressed as kmph or mph.
c. Rate of March. Rate of march is the average number of kilometers or miles traveled in any specific time period. It includes short periodic halts and short delays, but it does not include long halts, such as those for consuming meals or for overnight stops. It is expressed in kilometers or miles in the hour (kmih or mih).
E-5. TIME AND DISTANCE FACTORS. Time and distance factors (see Figure E-4) are used to perform a wide range of calculations for planning highway movements. They can be used to conduct detailed planning to develop movement tables. They can also be used to conduct expedient planning and calculating to manage movement request as discussed in paragraphs E-6 and E-7.
a. Distance Factors. Distance factors are expressed in kilometers or meters. The terms used to describe distance factors are as follows:
- Length of any column or element of a column is the length of roadway which it occupies. It is measured from the front bumper of the lead vehicle to the rear bumper of the trail vehicle and includes all gaps inside the column.
- Road space is the length of a column, plus any additional space (safety factor) added to the length to prevent conflict with preceding or succeeding traffic.
- Gap is the space between vehicles, march units, serials, and columns. It is measured from the trail vehicle of one element to the lead vehicle of the following element. The gap between vehicles is normally expressed in meters. The gap between march elements is normally expressed in kilometers.
- Lead is the space between the heads of elements in a convoy or between heads of successive vehicles, march units, serials, or columns.
- Road distance is the distance from point to point on a route, normally expressed in kilometers.
- Road clearance distance is the distance that the head of a column must travel for the entire column to clear the RP or any point along the route. Route clearance distance equals the column's length or road space plus road distance.
b. Time Factors. Time is expressed in hours or minutes. The terms used to describe time factors are as follows:
- Pass time (or time length) is the time required for a column or its elements to pass a given point on a route.
- Time space is the time required for a column or its elements to pass any given point on a route plus any additional time (safety factor) added to the pass time.
- Time gap is the time measured between vehicles, march units, serials, or columns as they pass a given point. It is measured from the trail vehicle of one element to the lead vehicle of the following element.
- Time lead is the time measured between individual vehicles or elements of a column, measured from head to head, as they pass a given point.
- Time distance is the time required for the head of a column or any single vehicle of a column to move from one point to another at a given rate of march.
- Road clearance time is the total time a column or one of its elements requires to travel the road distance and clearance point along the route or the RP. Road clearance time equals the column's pass time or time space plus time distance.
Figure E-4. Time and Distance Factors
E-6. TIME, DISTANCE, AND RATE CALCULATIONS. Time, distance, and rate factors are used to make scheduling calculations for columns of any size. When two of the three factors are known, the third can be found by using one of following equations as shown in Figure E-5.
Figure E-5. Finding an Unknown Factor of Time, Distance, or Rate
a. Determining Time. Time equals distance divided by rate. If the distance is 210 km and the rate of march is 42 kmih, the time is 5 hours: 210 ¸ 42 = 5.
b. Determining Distance. Distance equals rate multiplied by time. If the rate of march is 40 kmih and time is 4 hours, the distance is 160 km: 40 x 4 = 160.
c. Determining Rate. Rate equals distance divided by time. If a convoy travels for 5 hours to complete a 190 km trip, its rate of march is 38 kmih: 190 ¸ 5 = 38.
E-7. ARRIVE AND CLEAR TIME CALCULATIONS. To manage movements on MSRs by using location or column scheduling, movement control organizations can use an expedient method of planning and calculating. Both requestors and movement control organizations must understand and apply time and distance factors associated with the movement of convoys on MSRs. Moving units must make calculations as part of their movement planning and movement requests.
The minimum essential information needed is the arrive and clear times at SPs, intermediate CPs, and RPs. Therefore, TA, Corps, and division SOPs should specify a clearance request format that requires requesting units to calculate these arrive and clear times (see Figure E-6). The DTO, HTD, or MCB may have to perform these calculations for large unit movements or special movements. They should check the accuracy of unit requests.

Figure E-6. Sample Movement Bid
Figure E-6. Sample Movement Bid (continued)
Use time, distance, and rate factors to calculate arrive and clear times. The arrive time is the time the first vehicle in the column will reach an SP, CP, or RP. The arrive time is derived from calculating the time distance. The clear time is the time the last vehicle in the column will clear that SP, CP, or RP. The clear time is derived from calculating the pass time.
Calculate arrive times as follows:
- To calculate the arrive time at the first CP (see also Table E-1), take the distance from the SP to the first CP, divide by the planned rate of march, and multiply by 60 minutes.
Table E-1. Calculating Arrive Times (First CP)
|
- To calculate the arrive time at the second CP (see also Table E-2), take the distance from the first CP to the second CP, divide by the rate of march, and multiply by 60.
Table E-2. Calculating Arrive Times (Second CP)
|
NOTE: Continue this method to calculate the arrive time at succeeding CPs through the RP.
To calculate the clear times at each CP, planners must determine the pass time. Calculating pass time requires calculations for density (Table E-3), time gaps (Table E-4), road space (Table E-5), and pass time (Table E-6).
Table E-3. Calculating Pass Times (Density)
| ||||||||||||
Table E-4. Calculating Pass Times (Time Gaps)
Note: Time gaps = ([number of march units - 1] x march unit time gap) + ([number of serials - 1] x [serial time gap - march unit time gap]).
|
Table E-5. Calculating Pass Times (Road Space)
| ||||||||||||||||||||||||||||||||||||
Table E-6. Calculating Pass Times (Pass Time)
| |||||||||||||||||||||||||||||||
The pass time at the SP is 42 minutes after the first vehicle crosses the SP. If the arrive time at the SP is 0800, the clear time at the SP will be 0842. If the arrive time at the first CP is 0816, the clear time at the first CP will be 0858. Use this same method to calculate the arrive and clear times at succeeding CPs to the RP.
The pass time will stay the same throughout the route as long as the march rate and density do not change. If the march rate or density changes, then recalculate the pass time to determine the new clear time. Calculations are simplified by the following:
- Preparing and using conversion tables for changing US common distances to metric distances, number of vehicles to pass time, and distance to time.
- Standardizing variables to reduce calculation time. When possible, use standard march rates and density.
- Using automated programs to calculate arrive and clear times such as the military application program package.
Section III. Preparing Movement Tables for a Highway Movement
E-8. REVIEWING THE SITUATION. This section provides a step-by-step example of how to compute a highway movement, prepare a road movement graph, and prepare road movement tables for a convoy consisting of five serials.
a. Convoy Data. On 23 February, elements of the 439th Transportation Battalion will move from the unit's present position to an area near CP 106. The movement will consist of five serials, organized as shown in Figure E-7. The first and second serials have six march units each; the third and fourth serials have seven march units each; and the fifth has five march units. The SP is CP 97, and the RP is CP 106. The route of march is from CP 97 to CP 106 by way of CPs 99, 103, 104, and 105. The lead vehicle of the first serial will cross the SP at 0800.
|
SERIALS |
UNIT |
NUMBER OF VEHICLES |
NUMBER OF MARCH UNITS |
First |
2439th and 2440th Transportation Companies |
126 |
6 |
Second |
2441st and 2442d Transportation Companies |
135 |
6 |
Third |
2443d and 2444th Transportation Companies and Headquarters and Headquarters Detachment, 439th Transportation Battalion |
150 |
7 |
Fourth |
2445th and 2446th Transportation Companies |
144 |
7 |
Fifth |
2447th and 2448th Transportation Companies (attached) |
124 |
5 |
Figure E-7. Organization of Serial March Units
b. Movement Conditions. Extracts of the highway regulation plan specify the following conditions on the movement.
- The rate of march during daylight hours is 24 kmih and the density of vehicles during daylight hours is 12 per km.
- The rate of march during hours of darkness (1835 to 0630) is 16 kmih and the density of vehicles during hours of darkness is 48 per km.
- Gaps will be 10 minutes between serials and 2 minutes between march units.
- When an en route restriction is applied to the movement, a 15-minute safety factor will be allowed before and after the restriction.
c. Restrictions. The following restrictions are in effect on 23 February.
- CP 99 to CP 103 from 1100 to 1200.
- CP 105 from 1500 to 1530.
- CP 104 from 1510 to 1630.
- CP 105 from 1700 to 1830.
d. Additional Guidance. The fourth serial will halt in place at the 1500 to 1530 restriction at CP 105 and will continue as soon as possible after the restriction. The head of the fifth serial will depart the SP as soon as possible to clear the restriction at CP 104. The fifth serial will stop at the 1700 to 1830 restriction at CP 105 and disperse vehicles until the restriction is lifted.
NOTE: All computations in minutes resulting in a fraction are raised to the next full minute; km are rounded up to the nearest tenth. For example--
- 15.6 minutes - 16 minutes.
- 15.3 minutes - 16 minutes.
- 13.67 km = 13.7 km.
- 13.43 km = 13.5 km.
E-9. COMPUTING TIME DISTANCE OF THE ROUTE. The planner must first determine how long it will take each serial to travel from the SP to the RP, the time distance of the route.
a. Formula. Compute the time distance by dividing the distance from the SP to the RP by the rate of march (TD = D+ R).
b. Data. The distances between CPs and total distance are shown in Table E-7.
Table E-7. CP Distances
|
c. Computation. The distance from SP to RP is 75 km. The lead vehicle will cross the SP at 0800 and the rate of march during daytime is 24 kmih. Substituting in the formula TD = D + R, TD = 75 + 24, or 3.125 hours. Since .125 hours is 8 minutes (.125 X 60), the time distance is 3 hours and 8 minutes.
E-10. COMPUTING ROAD SPACE OF THE FIRST SERIAL. Road space is the length of a column. The formula for computing road space is shown in Table E-8. Figure E-7 shows 126 vehicles in the first serial. The rate of march is 24 kmih; the density is 12 vehicles per kilometer. The time gap is 2 minutes between march units. Because six march units make up the serial, there are five gaps making a total time gap in the serial of 10 minutes. The formula for computing road space for the first serial is shown in Table E-9.
Table E-8. Computing Road Space
|
Table E-9. Computing Road Space (First Serial)
|
E-11. COMPUTING PASS TIME OF THE FIRST SERIAL. Pass time is the time required for a column to pass a point on the route. The formula for computing pass time is shown in Table E-10. Use the road space computed in Table E-9 (14.5 km) to compute road space (Table E-11).
Table E-10. Computing Pass Time
|
Table E-11. Computing Road Space
|
E-12. COMPUTING ROAD SPACE AND PASS TIME OF THE SECOND, THIRD, FOURTH, AND FIFTH SERIALS. Using the same formulas and methods of computation as for the first serial, compute the road space and pass time for the second serial (Table E-12), third serial (Table E-13), fourth serial (Table E-14), and fifth serial (Table E-15).
Table E-12. Computing Road Space and Pass Time (Second Serial)
|
|
Table E-13. Computing Road Space and Pass Time (Third Serial)
|
|
Table E-14. Computing Road Space and Pass Time (Fourth Serial)
|
|
Table E-15. Computing Road Space and Pass Time (Fifth Serial)
|
|
E-13. PUBLISHING ROAD MOVEMENT TABLES. The road movement graph is a planning work sheet for movement planners. It is not normally disseminated to subordinate units or published in plans and orders. Information obtained from the graph is published in road movement tables.
E-14. PREPARING A ROAD MOVEMENT GRAPH. A road movement graph is a time and space diagram. After computing for a move, the planner can then see where he plotted the move. The following explains how to plot the move.
a. Designating Hours. From the lower left corner across the bottom of the graph designate the time needed for the movement. Since the first serial is to arrive at the SP at 0800, the timing of this graph should start at 0800 in the lower left corner. The computations performed in paragraphs E-10, E-11, and E-12 show that more than 12 hours are required to complete the movement of the five serials. This is derived from adding the time distance, sum of pass times, restricted times, and gaps. Therefore, the time of this graph must extend to at least 2100. In this example, each horizontal block represents 12 minutes and every six blocks represents 1 hour as shown in Figure E-8.
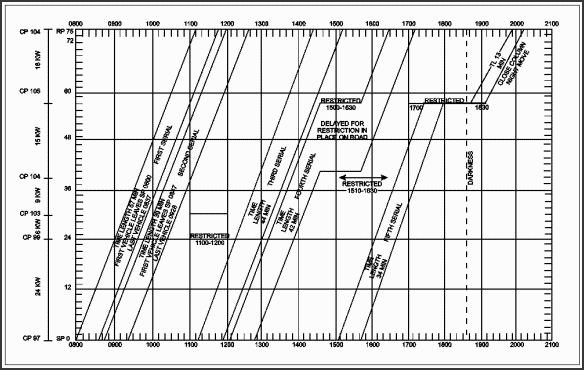
Figure E-8. Road Movement Graph for Five Serials
b. Designating Kilometers. Indicate the distance to be moved in kilometers on the vertical axis. Begin at the SP in the lower left corner of the graph with 0 km. Since this move is 75 km, the top of the vertical axis should be marked as 75 km. In this example, each vertical block between 0 and 75 km represents 1.5 km as shown in Figure E-8. It is important to show critical points, checkpoints, or other important points directly opposite the correct distance blocks of the graph. For example, CP 99 is 24 km from the SP and is noted on the scale opposite the 24 km line. CP 103 is noted on the scale opposite the 30 km line.
c. Plotting the Restrictions. Mark route restrictions within the graph as described below.
(1) The first restriction is from CP 99 to CP 103 between 1100 and 1200. CP 99 is 24 km (16 blocks) from the SP and CP 103 is 6 km (4 blocks) from CP 99. To show the restriction, the time from 1100 to 1200 between CP 99 and CP 103 is blocked out.
(2) The second restriction is at CP 105 between 1500 and 1530. CP 105 is at the 57 km point. In this example, the restriction is only at the CP. To show the restriction, a horizontal line from 1500 to 1530 at the CP is marked. It extends horizontally form 1500 over three blocks (30 minutes).
(3) The third and fourth restrictions are also only at the CP. They are shown as above.
E-15. GRAPHING THE FIRST SERIAL. Once the hours, kilometers, and restrictions are marked on the graph, plot the serials. The first vehicle of the first serial is scheduled to leave the SP at 0800. Put a dot at the beginning of the 0800 line in the lower left corner of the graph. Figure E-8 shows the first vehicle is to arrive at the RP at 1108. This was calculated by adding the time distance (3 hours and 8 minutes) to the time the first vehicle crosses the SP. Locate the 1108 hour line at the top of the graph at the RP (75 km line) and put a dot there and then connect the dots.
The next step is to plot the trail (last vehicle) of the first serial. To find the time the last vehicle crosses the SP, add the pass time to the time the first vehicle crosses the SP. As determined in paragraph E-11, the pass time of the first serial is 37 minutes. Therefore, adding 37 minutes to 0800 gives 0837 as the time the last vehicle of the first serial leaves the SP. Make a dot at 0837 on the bottom of the graph. Then add the time distance of 3 hours and 8 minutes to 0837 start time to compute the time the last vehicle clears the RP. This is 0837 plus 3 hours and 8 minutes, or 1145. Make another dot at the top of the graph at 1145. Connect the dots. This second line parallels the first line drawn, which shows the movement of the first vehicle of the first serial. The horizontal space between the two lines represents the 37-minute pass time of the serial.
E-16. GRAPHING THE SECOND SERIAL. Because the last vehicle of the first serial is scheduled to clear the SP at 0837 and a 10-minute time gap is required between serials, the second serial cannot begin movement until 0847. To show the first vehicle of the second serial on the graph, place a dot at 0847 on the bottom of the graph. The time distance for the second serial is the same as that of the first serial. Therefore, the trail vehicle of the second serial will clear the RP at 1155 (0847 plus 3 hours and 8 minutes). To show the last vehicle of the second serial on the graph, place a dot at 1155 at the top of the graph at the RP and connect the dots with a line.
Plot the trail vehicle of the second serial the same as the first serial. To find the time the last vehicle of the second serial crosses the SP, add the pass time of the second serial to the time the first vehicle of the second serial crosses the SP. From Table E-12, this was determined to be 39 minutes. Therefore, adding 39 minutes to the 0847 SP time gives 0926 as the time the trail vehicle of the second serial leaves the SP. Make a dot at 0926 on the bottom of the graph. Since the first vehicle clears the RP at 1155 and the pass time is 39 minutes, the trail vehicle will clear the RP at 1234 (1155 plus 39 minutes). Make another dot on the top of the graph at 1234. Connect the two dots. The second serial is now complete.
E-17. GRAPHING THE THIRD SERIAL. Graphing the third serial is more complicated than the first two. The reason is that the third serial will not be able to clear the SP 10 minutes after the second serial clears the SP because this would cause it to run into the 1100 to 1200 restriction at CP 99. Therefore, compute for the earliest time the first vehicle can leave in order to pass the restriction after the restriction ends at 1200 (plus the 15-minutes safety factor). As shown in Figure E-8, the computation is 1200 (time the restriction ends) plus 15-minute safety factor minus 1 hour (time distance to the restriction [24 km at 24 kmih]) equals 1115. This time (1115) is the earliest time the first vehicle of the third serial can leave the SP. Place a dot at 1115 to show this SP time. Time distance is still 3 hours and 8 minutes. Therefore, the first vehicle of this serial will clear the RP at 1423. Put a dot at 1423 at the top of the graph and connect the two dots.
Since pass time for this serial is 44 minutes, the last vehicle will leave the SP at 1159. Time distance is still 3 hours and 8 minutes. Adding this to the starting time of the trail of the serial gives the clear time for the trail at the RP of 1507. Place dots at the times computed for the trail and connect them as with the two previous serials.
E-18. GRAPHING THE FOURTH SERIAL. Graphing the fourth serial is also more complicated than the others because it must halt at the 1500 to 1530 restriction at CP 105. The first step is to compute the time distance from the SP to the restriction. The distance is 57 km and the rate is 24 kmih. Using the formula to calculate time distance, TD = D +¸ R, 57 +¸ 24 = 2 hours and 23 minutes. Because the last vehicle of the third serial cleared the SP at 1159 and a 10-minute gap is required between serials, the fourth serial cannot begin movement until 1209.
The first vehicle of this serial will arrive at the restriction (CP 105) 2 hours and 23 minutes after it clears the SP, or 1423. Adding the pass time of this serial (42 minutes) to this gives 1514 as the time when the trail vehicle of the serial would clear CP 105 if it moved on without stopping. Since the restriction at this point is from 1500 to 1530, the column must halt at CP 105 and cannot move on until 15 minutes (safety factor) after the restriction ends. Thus the serial begins moving again at 1545.
The remaining distance of 18 km will take 45 minutes (18 km +¸ 24 kmih), so the lead vehicle clears the RP at 1630. The trail vehicle leaves CP 105, 42 minutes after the lead vehicle at 1627 and clears the RP, 45 minutes later at 1712.
E-19. GRAPHING THE FIFTH SERIAL. For the fifth vehicle, as with the third serial, a 10-minute time gap will not work because the fourth serial will be halted on the road for the restriction at CP 104. If the fifth serial was to leave 10 minutes after the fourth serial cleared the SP, it would run into the fourth serial at its halt.
Therefore, compute the earliest time the lead vehicle can leave the SP in order to avoid running into the fourth serial at CP 104. As described in paragraph E-8, first find how long it takes the lead vehicle to travel the 39 km to CP 104: 39 km +¸ 24 kmih = 1 hour and 38 minutes. The restriction at CP 104 is in effect from 1510 to 1630. Adding the 15-minute safety factor, 1645 is the earliest time at which the lead vehicle of the serial can clear the restriction. Subtracting 1 hour, 38 minutes from 1645 gives 1507 as the earliest time the fifth serial can leave the SP. It will clear the CP 104 at 1645 without halting.
Another problem arises at this point. If the fifth serial leaves at 1507, it will arrive at CP 105 at 1730, 45 minutes after clearing CP 104. Since there is a 1700 to 1830 restriction at CP 105, the serial must halt and wait until 1845 to resume movement. Because this serial has been ordered to disperse off the road at CP 105, the halt is shown differently than with the fourth serial, which halted on the road and occupied road space.
The pass time of this serial must also be recomputed from this point since the movement instructions specified that a slower march rate and larger density apply to movements during darkness after 1835. Accordingly, the rate of march becomes 16 kmih, and vehicle density becomes 48 vehicles per kilometer. To find the new pass time, first calculate the new road space (see Table E-16). To recalculate the new pass time see Table E-17.
Table E-16. Calculating New Road Space
| ||||||||
Table E-17. Recalculating New Pass Time
|
Traveling at 16 kmih, it takes the lead vehicle 1 hour and 8 minutes to travel the remaining 18 km to the RP. It arrives there at 1953 (1845 + 1 hour and 8 minutes). The trail vehicle leaves CP 105, 18 minutes later than the lead vehicle, or at 1903; and arrives at the RP at 2011.
E-20. USING A ROAD MOVEMENT TABLE. Data is taken from the graph and put into a road movement table, which can be issued as an annex to an OPORD for a road movement. Convoy commanders can use the information to track their progress during movement and ensure they arrive and clear each CP on schedule. MRTs, TCPs, and others can use the information for control purposes.
Figure E-9 shows the front and back sides of a sample road movement table. The data in this table is derived from the information found on the graph in Figure E-8.

Figure E-9. Road Movement Table (Front)
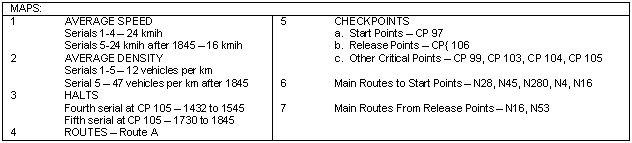
Figure E-9. Road Movement Table (Back)
Section IV. Road Management Planning
E-21. MOVEMENT PLANNING. Movement planners must manage the planned movement of convoys on controlled MSRs in order to issue movement credits, reroute, or divert. A critical time and point graph is a tool that may be used by movement planners to aid in preventing conflicts at critical points when planning and scheduling movements. It is an alternative method of managing movements from the grid system. Both methods accomplish the same function of tracking the planned itineraries of convoys as they arrive and clear planned checkpoints along MSRs. This method is more detailed and may be useful for planning movements on road networks that have many MSRs crossing each other.
E-22. CRITICAL TIME AND POINT GRAPH. Data for developing a critical time and point graph is taken from highway regulation plans or traffic circulation plans. These plans identify the critical points or checkpoints that will be used to plan movements. Movement planners also receive movement information for preplanned or immediate requirements. Preplanned information is derived from movement graphs or tables used to support the movement program. Immediate requirements are generated on short notice from clearance requests (movement bids).
The movement planner posts the movement data for each movement requirement to the critical time and point graph for the day or days involved. The planner will either confirm the availability of the road network for the requesting unit or makes changes to separate, balance, or distribute based upon command priorities.
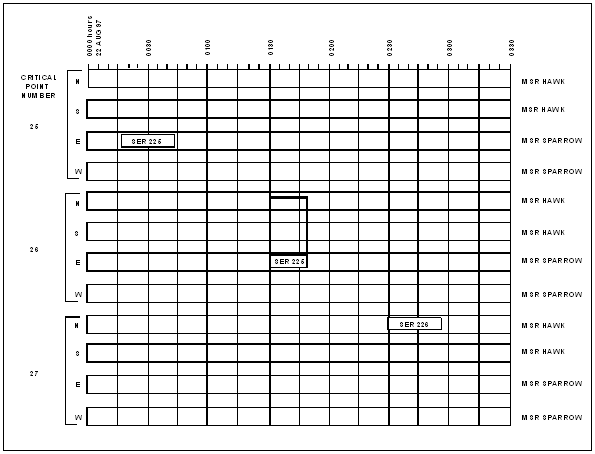
An example of a critical time and point graph is shown in Figure E-10. Critical time and point graphs are composed of subgraphs, one for each critical point. The name or number of the critical point is marked along the left margin. Each critical point has four paths, one for each direction (north, south, east, and west). These paths are marked along the left side to show the predominant direction of movement or change of direction. Time is annotated along the top on the vertical divisions of the graph in short time blocks, normally 15 minutes or less. A graph may reflect any time period. However, graphs do not normally exceed 24 hours.
The critical time and point graph reflects a route with three critical points (25, 26, and 27). In this example, the vertical lines represent five-minute time blocks. Two convoys are planned.
- Convoy 225 travelling eastward on MSR Sparrow will arrive at critical point 25 at 0020 and will clear that point at 0040. Therefore, the block representing convoy 225 extends from the arrive time to the clear time.
- Convoy 225 then continues to travel eastward and will arrive at critical point 26 at 0130. At critical point 26, convoy 225 turns northward on MSR Hawk as shown by the flag extending from the eastbound to northbound paths. Changes in direction of travel at critical points are always indicated by a flag extending into the appropriate path on the graph opposite N, S, E, W. Convoy 225 clears critical point 26 about 0145.
- Convoy 226 travelling northward on MSR Hawk arrives at critical point 27 at 0230 and will clear that point at 0300.
Figure E-10. Critical Time and Point Graph
Critical time and point graphs should be prepared for each MSR in advance for a specified planning period to manage programmed moves over multiple routes. The data for arrive and clear times at critical points can be obtained from movement graphs, movement bids, or automated planning programs such as MOVEPLAN. The planning period will vary depending upon the level of command. Generally, the MCA and MCB work with longer planning periods than does the DTO because movements in the COMMZ and Corps rear area can be programmed further in advance.
On the day of movement, movement planners receive the in-transit status of convoys as reported by MRTs, TCPs, or the moving unit. They check the progress of movement against the critical time and point graph for that day. When a convoy is reported off schedule, they check the graph for time and space separations from other convoys. If necessary, planners may reroute or stop a movement or reschedule convoys to prevent conflicts. They provide these changes to the affected commands and the MPs.
|
NEWSLETTER
|
| Join the GlobalSecurity.org mailing list |
|
|
|